Histogramme et courbe de densité de Kernel

Megbe Karamoko et Ibrahima Ousmane Ida

2015-04-13

Version PDF de cette page web : histogramme_ggplot2.pdf

1 Présentation de type de graphique

1.1 Histogramme

En analyse des données, il est opportun de faire des représentations graphiques des données. Cela nous donne une idée de la forme des distributions, des statistiques de localisation (moyenne, écart-type, …), des valeurs aberrantes, etc. L’une des représentations courantes est l’histogramme. C’est un outil d’exploration qui montre la distribution des données groupées en un ensemble de rectangles (ou intervalles). Chaque rectangle de l’histogramme représente une classe de données et sa base correspond à la longueur de l’intervalle et la surface du rectangle traduit la fréquence de la classe pour une représentation avec fréquence en ordonnée ou la proportion pour une représentation avec la probabilité en ordonnée. Le nombre de classes a un impact important sur le graphique de l’histogramme des données. Ce nombre peut se calculer selon des règles. Les plus utilisées sont: règle de Sturges, règle de Scott et règle de Freedman-Diaconis. Les logiciels statistiques utilisent par défaut la règle de Sturges.

1.2 Courbe de densité de Kernel

En statistique, l’estimation par noyau (ou encore courbe de densité de Kernel) est une méthode non paramétrique d’estimation de la densité de probabilité d’une variable aléatoire. Elle est relative à l’histogramme; elle permet de représenter un ensemble de données. En effet, la densité de Kernel offre une possibilité d’estimer la distribution sur des données. En d’autres termes, elle estime la fréquence sur ces données.
La courbe de densité de Kernel constitue alors la représentation en forme de ligne lisse de cette distribution estimée sur les données. La forme de la courbe dépend fortement du paramètre de lissage (appelé en anglais bandwidth ou window width) ou encore le type du noyau. Parmi les types du noyau, nous pouvons citer entre autres le noyau Epanechnikov, le noyau Gaussien, le noyau triangulaire, le noyau rectangulaire ou uniforme, etc. La plupart des logiciels statistiques ont par défaut le noyau gaussien. C’est ce noyau que nous allons utiliser par la suite pour l’estimation de la densité.

1.3 Application aux données

Notre démonstration va consister à produire d’abord un graphique simple en utilisant des fonctions graphiques de base en R accompagné d’explications, ensuite un graphique simple avec des fonctions du package ggplot2 accompagné d’explications et finalement un graphique avancé en utilisant des fonctions du package ggplot2 accompagné d’explications.

1.4 Présentation des données

Nous allons utiliser les données du fichier hour.csv de Bike Sharing Dataset téléchargeable sur le UCI Machine Learning Repository à l’adresse suivante : https://archive.ics.uci.edu/ml/datasets/Bike+Sharing+Dataset. Il s’agit de données concernant des nombres de locations de vélos par heure provenant d’un système de location de vélos dans la ville de Washington D.C. aux États-Unis. Plus précisément, nous nous intéressons aux données sur le nombre de locations effectuées entre 17h et 18h en 2011 et 2012.

# Manipulation des données 
# 1. Lecture du fichier de la table "hour.csv" des données
 data_base <- read.csv("hour.csv", header = TRUE, sep = ",") 
# 2. Extraction de la partie des données pour le travail,
# c'est à dire les données sur le nombre de locations entre 17h et 18h en 2011 et 2012.
donnees <- data_base[which(data_base$hr == 17), ]
# 3. Structure des données.Cela permet de voir le type des variables d'interêt  
str(donnees) 
## 'data.frame':    730 obs. of  17 variables:
##  $ instant   : int  18 41 63 86 109 132 155 179 203 227 ...
##  $ dteday    : chr  "2011-01-01" "2011-01-02" "2011-01-03" "2011-01-04" ...
##  $ season    : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ yr        : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ mnth      : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ hr        : int  17 17 17 17 17 17 17 17 17 17 ...
##  $ holiday   : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ weekday   : int  6 0 1 2 3 4 5 6 0 1 ...
##  $ workingday: int  0 0 1 1 1 1 1 0 0 1 ...
##  $ weathersit: int  2 1 1 1 1 1 2 1 1 1 ...
##  $ temp      : num  0.44 0.34 0.24 0.28 0.24 0.22 0.2 0.16 0.18 0.2 ...
##  $ atemp     : num  0.439 0.333 0.227 0.273 0.227 ...
##  $ hum       : num  0.82 0.57 0.3 0.48 0.38 0.51 0.37 0.37 0.37 0.4 ...
##  $ windspeed : num  0.284 0.194 0.224 0.224 0.194 ...
##  $ casual    : int  15 7 11 10 4 9 9 5 3 4 ...
##  $ registered: int  52 58 146 202 186 163 178 64 59 174 ...
##  $ cnt       : int  67 65 157 212 190 172 187 69 62 178 ...

Nos variables d’interêt sont cnt, yr, hr et weathersit. La variable yr concerne les années. Elle est de type entier et prend la valeur 0 pour 2011 et 1 pour 2012. Nous allons la rendre en facteur avec les niveaux 2011 et 2012.

donnees$yr <- as.factor(donnees$yr)
levels(donnees$yr) <- c("2011", "2012")

La variable weathersit contient les climats. Nous allons la renommer Temperature; elle est de type entier et prend les valeurs; 1: clair, partiellement nuageux, 2: brume + nuageux, brume + Peu de nuages, 3: neige légère, Pluie + orage + Peu de nuages, pluie + Éclaircies.

Nous allons la rendre en facteur avec les niveaux respectifs Dégagé, Nuage, brume, Pluie, neige.

colnames(donnees)[which(colnames(donnees) == "weathersit")] <- "Temperature"
donnees$Temperature <- as.factor(donnees$Temperature)
levels(donnees$Temperature) <- c("Dégagé", "Nuage, brume", "Pluie, neige")

À ce stade, nos données sont prêtes pour être exploitées adéquatement selon nos besoins.

str(donnees)
## 'data.frame':    730 obs. of  17 variables:
##  $ instant    : int  18 41 63 86 109 132 155 179 203 227 ...
##  $ dteday     : chr  "2011-01-01" "2011-01-02" "2011-01-03" "2011-01-04" ...
##  $ season     : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ yr         : Factor w/ 2 levels "2011","2012": 1 1 1 1 1 1 1 1 1 1 ...
##  $ mnth       : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ hr         : int  17 17 17 17 17 17 17 17 17 17 ...
##  $ holiday    : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ weekday    : int  6 0 1 2 3 4 5 6 0 1 ...
##  $ workingday : int  0 0 1 1 1 1 1 0 0 1 ...
##  $ Temperature: Factor w/ 3 levels "Dégagé","Nuage, brume",..: 2 1 1 1 1 1 2 1 1 1 ...
##  $ temp       : num  0.44 0.34 0.24 0.28 0.24 0.22 0.2 0.16 0.18 0.2 ...
##  $ atemp      : num  0.439 0.333 0.227 0.273 0.227 ...
##  $ hum        : num  0.82 0.57 0.3 0.48 0.38 0.51 0.37 0.37 0.37 0.4 ...
##  $ windspeed  : num  0.284 0.194 0.224 0.224 0.194 ...
##  $ casual     : int  15 7 11 10 4 9 9 5 3 4 ...
##  $ registered : int  52 58 146 202 186 163 178 64 59 174 ...
##  $ cnt        : int  67 65 157 212 190 172 187 69 62 178 ...

2 Histogramme et Courbe de densité avec des fonctions R de base

2.1 Histogramme avec des fonctions R de base

La principale fonction de base permettant de construire l’histogramme d’un vecteur d’observations en R est la fonction hist. Elle comporte plusieurs arguments permettant d’ajouter des détails à l’histogramme ou spécifier le type de fréquences (simples ou relatives) qui seront utilisées. Parmi ceux-ci, il y a notamment les arguments: breaks pour le nombre de classes, freq pour une représentation de fréquence en ordonnée,probability pour une représentation de probabilité en ordonnée, main pour le titre, xlab pour le nom de l’axe des abscisses, ylab pour le nom de l’axe des ordonnées, etc.

La commande ci-dessous permet de représenter l’histogramme de la distribution du nombre de locations effectuées entre 17 h et 18 h en 2011 pour le climat dégagé.

hist(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"])

Nous allons ajouter progressivement les arguments freq, main, xlab, ylab à l’histogramme.

On peut choisir de construire l’histogramme avec des fréquences relatives au lieu des fréquences simples grâce à l’argument freq.

hist(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"], 
     breaks = 13, freq = FALSE)

Pour donner un titre à l’histogramme et nommer les axes, nous allons utiliser les arguments main, xlab et ylab.

hist(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"],
     breaks = 13, freq = FALSE, 
     main = "Densité empirique du nombre de locations entre 17h et 18h en 2011 par temps dégagé",
     xlab = "nombre de locations entre 17h et 18h", ylab = "densité")

2.2 Courbe de densité avec des fonctions R de base

La fonction density de R de base permet de calculer la densité de Kernel pour estimer la distribution sur des données.

Pour illustrer cela, nous allons calculer la densité du nombre de locations en 2011 par climat dégagé par la commande suivante:

densite <- density(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"])
plot(densite)

2.3 Surperposition de l’histogramme et la densité de kernel

Représentons sur le même graphique l’histogramme et la courbe de densité à l’aide de la fonction lines.

hist(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"], 
     breaks = 13, freq = FALSE, 
     main = "Densité empirique du nombre de locations entre 17h et 18h en 2011 par temps dégagé", 
     xlab = "nombre de locations entre 17h et 18h", ylab = "densité")
densite <- density(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", "cnt"])
lines(densite)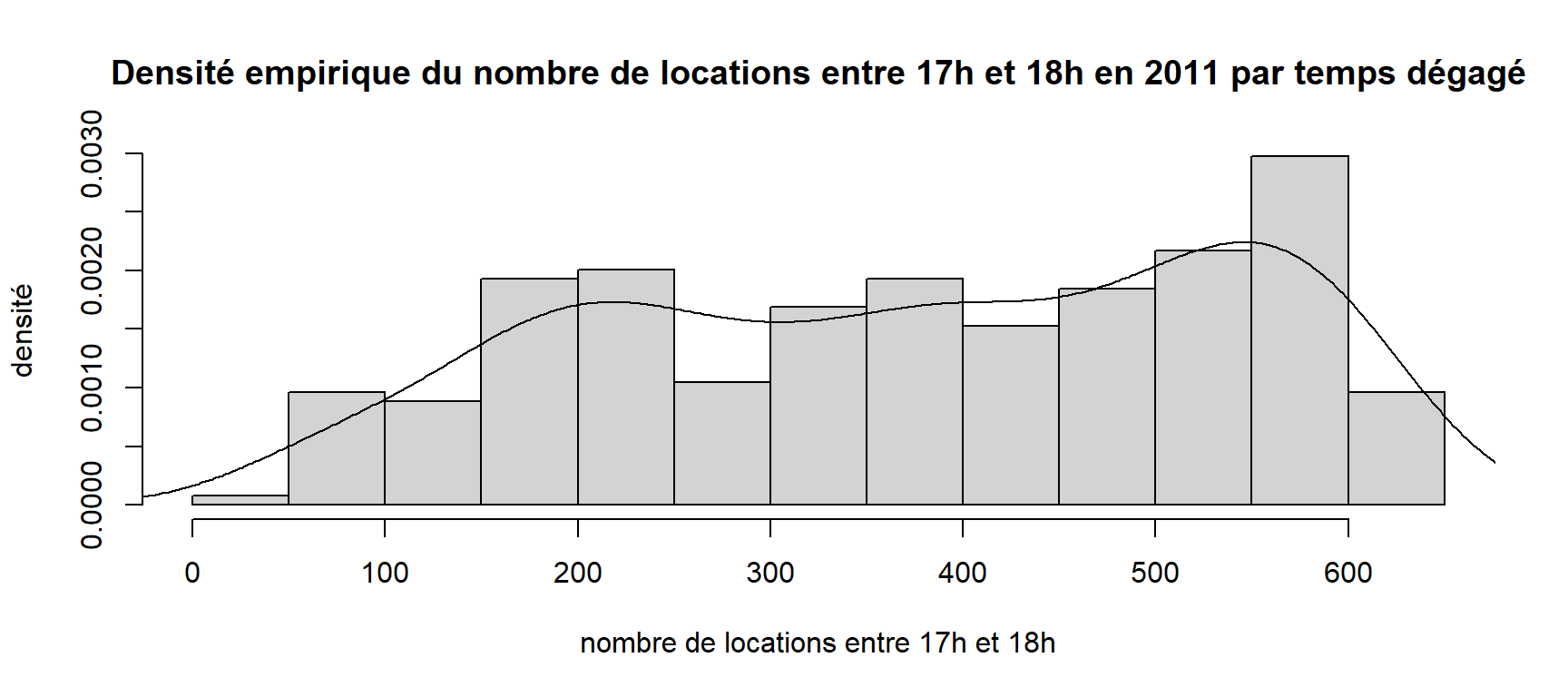

3 Histogramme et courbe de densité avec le package ggplot2

L’histogramme et la courbe de densité représentés précédemment peuvent facilement être reproduits en utilisant des fonctions du package ggplot2. Cette reproduction peut être scindée en deux étapes: une première étape pour dessiner l’histogramme et la seconde pour représenter la courbe de densité. Dans ggplot2, nous retenons deux méthodes pour représenter les graphiques notamment avec les fonctions qplot et ggplot. Ces fonctions définissent les parcelles dédiées à la représentation graphique. La méthode avec qplot offre une rapidité de programmation et une utilisation interactive. Cependant, la fonction ggplot est plus complète en syntaxe. Elle est plus facile à utiliser pour les personnes déjà familières avec les fonctions graphiques R de base. Pour illustrer, les commandes suivantes permettent de produire deux histogrammes, l’un avec la fonction qplot et l’autre avec la fonction ggplot:

# Il faut tout d'abord charger le package ggplot2
library(ggplot2)
qplot(cnt, data = donnees, geom = "histogram")

ggplot(donnees, aes(x = cnt)) + geom_histogram()

Les deux histogrammes précédents sont produits avec les paramètres par défaut de ggplot2. Ils permettent simplement de montrer le résultat que donnent les fonctions qplot et ggplot. Mais, dans la suite du travail, toutes représentations graphiques seront faites avec la fonction ggplot.

3.1 Histogramme avec la fonction ggplot

La fonction ggplot du package ggplot2 permet de produire une zone graphique à laquelle on peut ajouter des couches graphiques. La fonction qui sert à ajouter une couche d’histogramme est la fonction geom_histogram. Cette dernière comprend des arguments tels que stat, fill, position, linetype, size, colour, etc. qui permettent de définir les caractéristiques de l’histogramme et de lui ajouter des détails pour l’améliorer.

Créons la zone graphique avec la fonction ggplot et ses deux arguments data et aes permettent de préciser les données qui seront utilisées et la variable à représenter.

# Création de la zone graphique. 
zone <- ggplot(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", ], aes(x = cnt))

Nous allons ajouter la couche de l’histogramme avec la fonction geom_histogram. L’argument colour donne la possibilité de choisir la couleur des lignes des rectangles de l’histogramme, fill la couleur de remplissage et binwidth la largeur des rectangles. L’argument aes spécifie le type de fréquences utilisées.

Note: La fonction theme_classic() permet d’obtenir un fond graphique classique, c’est-à-dire un fond blanc sans quadrillage.

zone <- ggplot(donnees[donnees$yr == "2011"&donnees$Temperature == "Dégagé", ], aes(x = cnt)) 
zone + geom_histogram(aes(y = ..density..), colour = "black", fill = "white", binwidth = 50) + 
  theme_classic()

Nous allons maintenant ajouter un titre au graphique et nommer les axes avec la fonction labs.

zone <- ggplot(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", ], aes(x = cnt)) 
zone + geom_histogram(aes(y = ..density..), colour = "black", fill = "white", binwidth = 50) + 
  theme_classic() + 
  labs(title = "Densité empirique du nombre de locations entre 17h et 18h en 2011 par temps dégagé",
       x = "nombre de locations entre 17h et 18h", y = "densité")

3.2 Courbe de densité avec la fonction ggplot

Pour compléter le graphique, nous allons ajouter la courbe de densité. Pour ce faire, utilisons la fonction geom_density:

zone <- ggplot(donnees[donnees$yr == "2011" & donnees$Temperature == "Dégagé", ], aes(x = cnt)) 
zone + geom_histogram(aes(y = ..density..), colour = "black", fill = "white", binwidth = 50) + 
  theme_classic() + 
  labs(title = "Densité empirique du nombre de locations entre 17h et 18h en 2011 par temps dégagé", 
       x = "nombre de locations entre 17h et 18h", y = "densité") + 
  geom_density() + 
  xlim(0, 750)  
## Warning: Removed 2 rows containing missing values (geom_bar).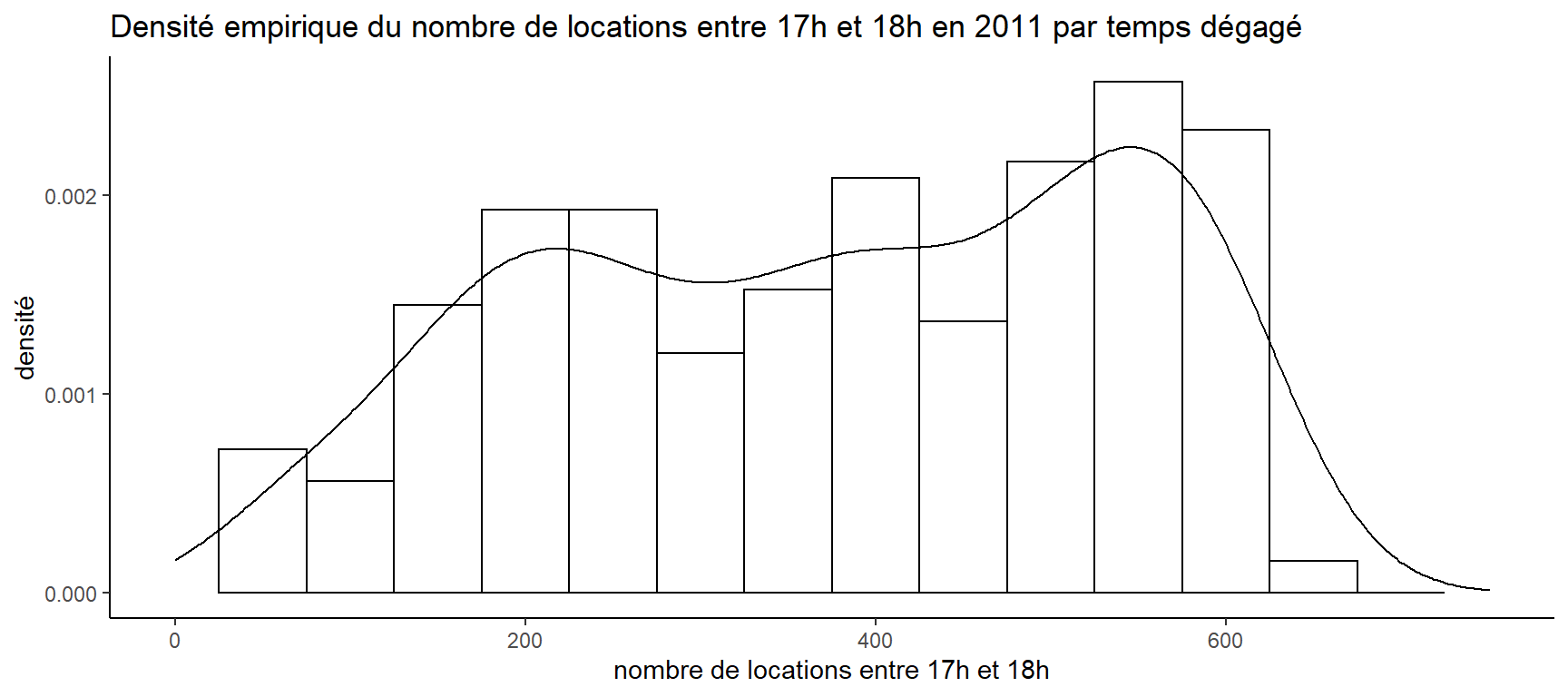

4 Graphique avancé avec ggplot2

La fonction ggplot permet également de produire des graphiques juxtaposés comprenant plusieurs représentations de densité de Kernel. Pour ce faire, lorsqu’on utilise la fonction ggplot, il faut lui joindre les fonctions geom_density et facet_grid. La fonction facet_grid permet de juxtaposer les graphiques soit verticalement, soit horizontalement. L’argument fill, de la sous-fonction aes contenue par geom_density, permet de représenter plusieurs courbes sur le même graphique.

La commande suivante permet de produire deux graphiques côte à côte sur le nombre de locations réalisées en 2011 et 2012.

zone <- ggplot(donnees, aes(cnt)) 
zone +  geom_density(aes( fill = Temperature),alpha = 0.7) + 
  xlim(0, 1000) +
  facet_grid(. ~ yr)

L’argument fill permet de distinguer les courbes selon la température qu’il fait. La fonction facet_grid et l’argument . ~ permettent de spécifier et de juxtaposer verticalement les graphiques en fonction des années. Il faut noter que l’argument alpha de la fonction geom_density permet de définir le niveau de transparence de remplissage des aires sous les courbes de densité. La fonction xlim, quant à elle, définit l’étendue de l’axe des abscisses.

Nous pouvons nous servir des fonctions ggtitle pour ajouter un titre, xlab et ylab pour nommer les axes et guides pour ajouter la légende. Il faut noter que la fonction theme avec l’argument legend.position permet de préciser où la légende sera placée.

zone <- ggplot(donnees, aes(cnt))
zone + geom_density(aes( fill = Temperature),alpha = 0.7) + 
  xlim(0, 1000) +
  facet_grid(. ~ yr) + 
  ggtitle("Densité empirique du nombre de locations entre 17h et 18h en 2011 par temps dégagé") + 
  xlab("nombre de locations entre 17h et 18h") + 
  ylab("densité de Kernel") + 
  guides(fill=guide_legend(
    title.position="left",label.position="right",label.hjust=0.5,direction="horizontal")
    ) + 
  theme(legend.position="bottom")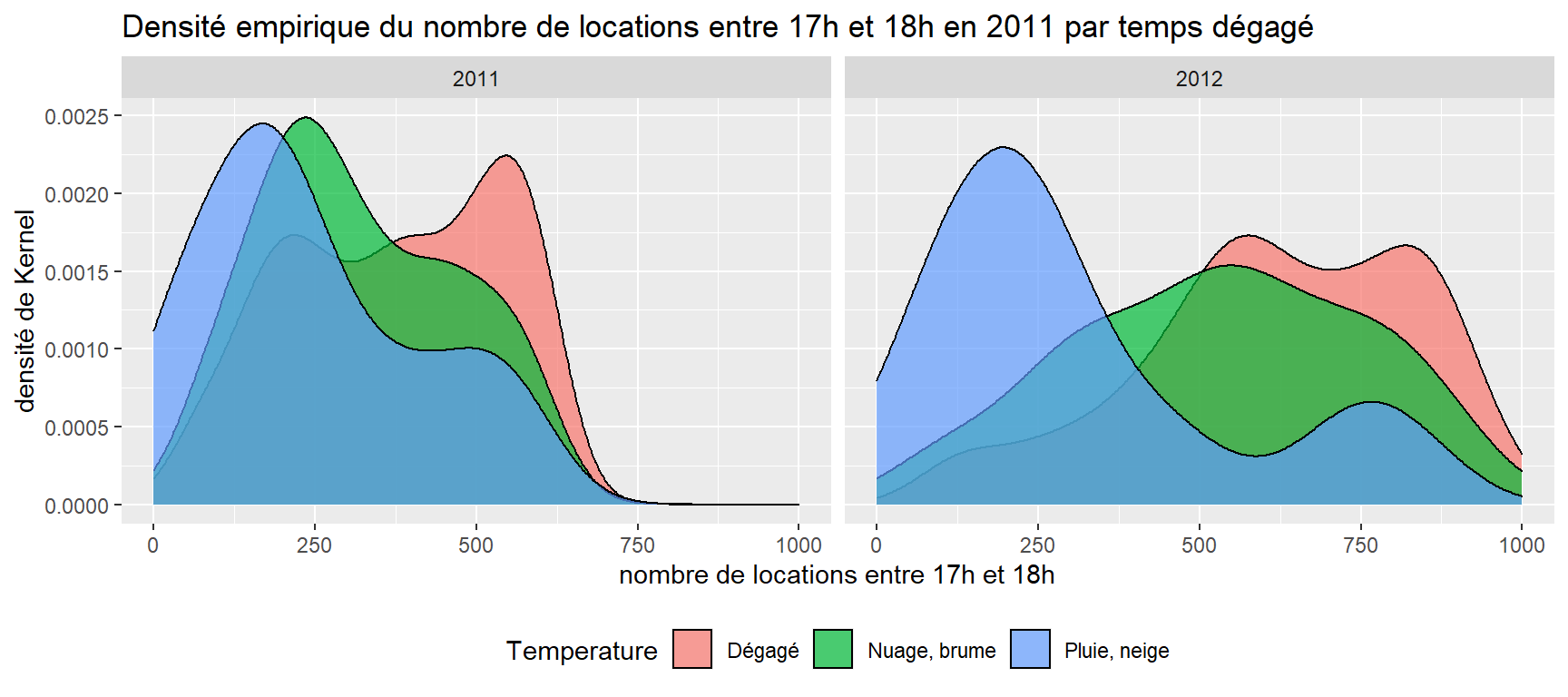

Références