1.1 Nombres décimaux

Voici quelques exemples de tours que peut nous jouer l’imprécision numérique en R sur des nombre décimaux (exemples tirés de [1]).

Pourquoi la commande suivante ne retourne-t-elle pas TRUE?

.1 == .3/3

## [1] FALSE

Pourquoi le 4^e élément du vecteur suivant n’est-il pas TRUE?

seq(0, 1, 0.1) == .3

##  [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

Pourquoi la longueur de cet objet n’est-elle pas 1?

unique(c(.3, .4 - .1, .5 - .2, .6 - .3, .7 - .4))

## [1] 0.3 0.3 0.3

Parce R a une précision limitée pour garder des nombres en mémoire. Nous sommes portés à croire que 0.1 en R est réellement le nombre 0.1, soit un dixième (1/10), mais en fait R a stocké en mémoire la valeur suivante :

print(.1, digits = 20)

## [1] 0.10000000000000001

alors que .3/3 a été stocké en mémoire comme suit :

print(.3/3, digits = 20)

## [1] 0.099999999999999992

donc ces deux nombres ne sont pas exactement égaux! Par contre, ils sont approximativement égaux. D’où l’intérêt d’être « tolérant » dans nos comparaisons entre deux nombres réels.

all.equal(.1, .3/3)

## [1] TRUE

x <- c(.3, .4 - .1, .5 - .2, .6 - .3, .7 - .4) 
x # même vecteur que précédemment

## [1] 0.3 0.3 0.3 0.3 0.3

print(x, digits = 20)

## [1] 0.29999999999999999 0.30000000000000004 0.29999999999999999 0.29999999999999999
## [5] 0.29999999999999993

table(x)

## x
## 0.3 
##   5

unique(x)

## [1] 0.3 0.3 0.3

print(unique(x), digits = 20)

## [1] 0.29999999999999999 0.30000000000000004 0.29999999999999993

factor(x)

## [1] 0.3 0.3 0.3 0.3 0.3
## Levels: 0.3

nlevels(factor(x))

## [1] 1

print(10^(-325))

## [1] 0

print(10^(-310))

## [1] 1e-310

10^(-325) / 10^(-310)

## [1] 0

10^(-310) / 10^(-325)

## [1] Inf

10^(-325 - -310)

## [1] 1e-15

1.2 Grands nombres en valeur absolue

Il faut aussi se méfier lorsque nous manipulons en R de grands nombres en valeur absolue.

100000000000000 + 1 == 100000000000000  # Ces deux nombres sont bel et bien différents.

## [1] FALSE

1e14 + 1 == 1e14  # Même comparaison, en notation scientifique.

## [1] FALSE

2^53 == 2^53 - 1  # Nous obtenons encore le résultat attendu.

## [1] FALSE

2^53 == 2^53 + 1  # Oups, c'est à partir d'ici que ça ne marche plus!

## [1] TRUE

Le plus grand nombre entier positif représentable en R 64 bits sur mon ordinateur est 2^53. Quel est ce nombre ?

print(2^53)

## [1] 9.007199e+15

Modifions l’option de la session R relative à la notation scientifique de façon à voir le nombre en notation fixe.

options(scipen = 10)
print(2^53)

## [1] 9007199254740992

Maintenant, observons un phénomène étonnant. Demandons à R d’afficher le nombre 2^53 + 1, soit 9007199254740993.

print(9007199254740993)

## [1] 9007199254740992

R affiche plutôt le nombre 2^53, soit 9007199254740992. Pourtant, ceci est correct :

print(9007199254740994)

## [1] 9007199254740994

Mais pas ceci :

print(9007199254740995)

## [1] 9007199254740996

L’explication à ces inexactitudes est que les nombres sont stockés dans la mémoire d’un ordinateur sous forme de bits. Cependant, le nombre de bits pouvant être utilisé pour stocker un nombre possède une limite maximale. Si le nombre à stocker requière plus de bits pour être représenté dans son intégralité que le nombre maximum de bits utilisables, il est légèrement arrondi.

La limite dans le nombre de bits utilisables en R pour stocker un nombre dépend du type de données utilisé pour le stocker (réel versus entier), du nombre de bits de la version de R utilisée (32 versus 64) ainsi que des spécifications de l’ordinateur utilisé. R 32 bits utilise moins de bits que R 64 bits.

Notez que la plus grande valeur représentable de 2^53 sur mon installation de R 64 bits s’applique à des nombres entiers d’un point de vue mathématique, mais stockés sous le type réel en R. Le type entier ne permet pas de représenter des nombres supérieurs en valeur absolue à l’objet R .Machine$integer.max (= 2147483647 sur mon installation de R 64 bits).

as.integer(-2147483647)

## [1] -2147483647

as.integer(-2147483647 - 1)

## Warning: NAs introduced by coercion to integer range

## [1] NA

options(scipen = 0)  # réattribution de sa valeur par défaut à l'option scipen

2.1 Chemin de recherche

À l’ouverture d’une session R, certains packages sont automatiquement chargés. Le contenu de chaque package chargé est placé dans ce qui est appelé un environnement. Les objets R que nous créons pendant une session R sont aussi conservés dans un environnement : l’environnement de travail (aussi appelé environnement courant ou environnement global). Lorsque R a besoin d’évaluer un objet apparaissant dans une expression soumise dans la console, il démarre une recherche de cet objet dans les environnements ouverts. La recherche débute dans l’environnement de travail. Si l’objet recherché n’est pas trouvé dans cet environnement, la recherche se poursuit dans les environnements des packages chargés, en commençant par les packages les plus récemment chargés.

La figure 1 illustre le chemin de recherche parcouru par R pour évaluer les expressions soumises dans la console. La recherche part de l’environnement du haut et descend dans les environnements en dessous, jusqu’à ce que l’objet recherché soit trouvé. C’est le nom d’un objet qui permet de l’identifier.

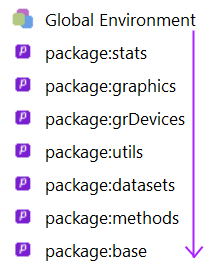
Figure 2.1: Chemin de recherche parcouru par R pour évaluer les expressions soumises dans la console

Il existe quelques exceptions à cette façon de rechercher la valeur d’expressions en R. Les sous-sections suivantes décrivent quelques-unes de ces exceptions.

2.2 Évaluation d’un appel à une fonction

Lors de l’évaluation d’un appel à une fonction, des environnements s’ajoutent au début du chemin de recherche décrit ci-dessous, uniquement le temps de l’évaluation de la fonction. Tous les détails sont fournis dans les notes sur les fonctions en R.

2.3 Fonctions ajoutant un data frame au début du chemin de recherche

Les fonctions R prenant en entrée une formule, prennent aussi toutes en entrée un argument data. Si un data frame est donné à cet argument, ce data frame devient un environnement de plus, qui s’ajoute à la liste des environnements parcourus lors de la recherche de la valeur d’un objet R. Cet environnement vient en premier dans la liste, la recherche débute donc par lui. Dans une formule, les noms des colonnes de data deviennent des objets directement accessibles (plus besoin d’utiliser la syntaxe data$nomColonne). Il en est de même dans l’expression fournie à l’argument subset souvent présent dans les fonctions prenant en entrée une formule.

Les fonctions subset et transform, que nous avons déjà vues, ainsi que toutes les fonctions du tidyverse possédant un argument data ou .data, ont le même genre de comportement. Le data frame (ou le tibble) donné au premier argument devient l’environnement d’où part la recherche des valeurs associées aux noms d’objets dans les expressions fournies aux arguments suivants.

Illustrons ce type d’évaluation avec la fonction subset. Supposons que nous voulons extraire du jeu de données iris du package datasets les observations de Petal.Length et Petal.Width pour lesquelles Sepal.Width est supérieure à 4, nous pouvons utiliser la commande

subset(iris, subset = Sepal.Width > 4, select = c(Petal.Length, Petal.Width))

##    Petal.Length Petal.Width
## 16          1.5         0.4
## 33          1.5         0.1
## 34          1.4         0.2

plutôt que

subset(iris, subset = iris$Sepal.Width > 4, select = c("Petal.Length", "Petal.Width"))

ou

iris[iris$Sepal.Width > 4, c("Petal.Length", "Petal.Width")]

La commande suivante ne fonctionne pas

iris[Sepal.Width > 4, c(Petal.Length, Petal.Width)]

## Error in `[.data.frame`(iris, Sepal.Width > 4, c(Petal.Length, Petal.Width)) : 
##   object 'Petal.Length' not found

parce que Sepal.Width, Petal.Length et Petal.Width sont des noms d’objets dont R doit trouver les valeurs. Le chemin de recherche parcouru par R pour trouver ces valeurs débute dans l’environnement de travail et se poursuit dans les environnements des packages chargés, en commençant par les packages les plus récemment chargés. R retourne une erreur, car il ne trouve nulle part ces objets. Il y a bien des colonnes du data frame iris qui portent les noms de ces objets, mais il ne s’agit pas d’objets directement accessibles. Ce sont des éléments dans un objet.

Dans la commande subset(iris, subset = Sepal.Width > 4, select = c(Petal.Length, Petal.Width)), R doit aussi trouver la valeur des objets Sepal.Width, Petal.Length et Petal.Width. Il trouve cette fois ces objets, car la fonction subset modifie le chemin de recherche de R (mais uniquement le temps de l’évaluation de l’appel à cette fonction). Elle ajoute au tout début du chemin de recherche un environnement, contenant les colonnes du data frame fourni comme premier argument. Dans l’exemple, l’environnement ajouté au chemin de recherche contient donc des vecteurs nommés "Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width" et "Species", soit les colonnes de iris.

Le chemin de recherche utilisé par R pour évaluer les expressions données à subset dans cet exemple est illustré dans la figure 2.

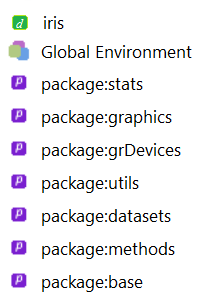
Figure 2.2: Chemin de recherche parcouru par R pour évaluer les expressions données en argument à la fonction subset dans l’exemple

var_catego <- cut(
  x = iris$Sepal.Length, 
  breaks = c(-Inf, quantile(iris$Sepal.Length, probs = c(1/3, 2/3)), Inf),
  right = FALSE
)
table(var_catego, iris$Species)

# équivalent à :

with(
  data = iris,
  expr = {
    var_catego <- cut(
      x = Sepal.Length, 
      breaks = c(-Inf, quantile(Sepal.Length, probs = c(1/3, 2/3)), Inf),
      right = FALSE
    )
    table(var_catego, Species)
  }
)

##             Species
## var_catego   setosa versicolor virginica
##   [-Inf,5.4)     40          5         1
##   [5.4,6.3)      10         31        12
##   [6.3, Inf)      0         14        37

head(women)

##   height weight
## 1     58    115
## 2     59    117
## 3     60    120
## 4     61    123
## 5     62    126
## 6     63    129

women2 <- 
  within(
    data = women,
    expr = {
      height <- height / 12
      weight2 <- weight^2
    }
  )
head(women2)

##     height weight weight2
## 1 4.833333    115   13225
## 2 4.916667    117   13689
## 3 5.000000    120   14400
## 4 5.083333    123   15129
## 5 5.166667    126   15876
## 6 5.250000    129   16641

2.4 Fonction attach

Certains d’entre vous connaissent peut-être la fonction attach. Cette fonction permet d’ajouter un data frame dans le chemin de recherche, juste en dessous de l’environnement de travail. Par exemple, la commande

attach(iris)

modifie le chemin suivant

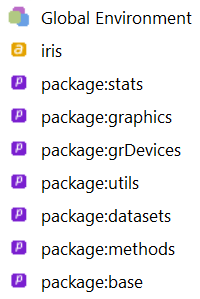
Je ne recommande pas l’utilisation de attach, car si l’environnement de travail contient déjà un objet portant le même nom qu’une colonne du data frame attaché, c’est l’objet dans l’environnement de travail qui sera retourné plutôt que la colonne du data frame si nous utilisons ce nom dans nos instructions. Ce comportement s’explique par le fait que l’environnement de travail demeure le point de départ du chemin de recherche avec attach, alors qu’avec with c’est le data frame qui est le point de départ du chemin de recherche.

Pour retirer du chemin de recherche un data frame attaché, il faut utiliser la fonction detach.

detach(iris)

2.5 Opérateur ::

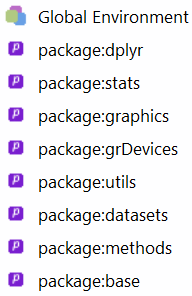
Plutôt que de laisser R parcourir tout son chemin de recherche pour retrouver un objet dans un environnement associé à un package, il est possible d’indiquer à R dans quel environnement chercher un objet avec l’opérateur :: (double deux-points). Cet opérateur est utile lorsque des fonctions sont masquées par un nouveau package chargé.

Par exemple, le package dplyr contient des fonctions portant le même nom que des fonctions des packages stats et base.

library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

Le chargement d’un nouveau package ajoute un environnement dans le chemin de recherche, juste en dessous de l’environnement de travail. Ainsi, la commande library(dplyr) a modifié le chemin suivant

Un appel à un des noms de fonction en double, par exemple à union, va utiliser par défaut la fonction union du package dplyr puisque l’environnement de ce package est plus haut dans le chemin de recherche que l’environnement du package base.

union

## function (x, y, ...) 
## UseMethod("union")
## <bytecode: 0x0000000013d0aa80>
## <environment: namespace:generics>

La dernière ligne de la sortie R générée identifie l’environnement de provenance de la fonction. Il s’agit de l’espace de noms du package generics. Il faut savoir ici que le package dplyr importe la fonction union du package nommé generics. Ainsi, la fonction union atteinte est bel et bien celle provenant du package dplyr. (Nous reviendrons sur les espaces de noms dans les notes sur l’utilisation de packages R.)

Pour accéder à la fonction union du package base avec le chemin de recherche courant, il faut utiliser l’opérateur :: comme suit.

base::union  # remarquez le nom de l'environnement de provenance de la fonction

## function (x, y) 
## unique(c(as.vector(x), as.vector(y)))
## <bytecode: 0x000000001f01de50>
## <environment: namespace:base>

En fait, nous pourrions toujours utiliser l’opérateur :: pour indiquer la provenance des fonctions que nous utilisons. Avec le chemin de recherche courant, le fonction union sélectionnée sans utilisation de l’opérateur :: est bel et bien celle provenant de dplyr, comme le prouve la sortie suivante.

dplyr::union

## function (x, y, ...) 
## UseMethod("union")
## <bytecode: 0x0000000013d0aa80>
## <environment: namespace:generics>

Notez que les auteurs du package dplyr ont délibérément repris des noms de fonctions du R de base. Il s’agit de versions de ces fonctions qu’ils jugent meilleures.

Un package peut être retiré du chemin de recherche avec la fonction detach comme suit :

detach("package:dplyr")

Notons que l’utilisation d’une fonction d’un package via l’opérateur :: ne requière pas que ce package soit chargé dans la session R. Il a simplement besoin d’être installé pour la version de R utilisée. Ainsi, même si nous venons de retirer le package dplyr du chemin de recherche, nous pouvons encore accéder aux fonctions qu’il contient, par exemple la fonction arrange, en utilisant l’opérateur ::, comme le prouve ce qui suit.

arrange

## Error in eval(expr, envir, enclos): object 'arrange' not found

dplyr::arrange

## function (.data, ..., .by_group = FALSE) 
## {
##     UseMethod("arrange")
## }
## <bytecode: 0x00000000160d00c8>
## <environment: namespace:dplyr>