STT-4230 > Calculs en R > Calculs statistiques en R

Calculs statistiques en R

Sophie Baillargeon, Université Laval

2021-02-24

Version PDF de cette page web : calculs_stat_r_2021.pdf

1 Statistiques descriptives
2 Distributions de probabilité
3 Génération de nombres pseudo-aléatoires
- 3.1 Fonction sample
- 3.2 Germe de la génération pseudo-aléatoire
4 Tests statistiques
5 Ajustement de modèles
- 5.1 Formules
  - 5.1.1 Exemples
  - 5.1.2 Arguments accompagnant les formules
- 5.2 Manipulation de la sortie
6 Résumé
Références

Note préliminaire : Lors de leur dernière mise à jour, ces notes ont été révisées en utilisant R version 4.0.3 et le package broom version 0.7.4. Pour d’autres versions, les informations peuvent différer.

R est un environnement spécialisé dans les calculs statistiques. Voyons comment réaliser de tels calculs en R, qu’il s’agisse de production de statistiques descriptives, de manipulation des distributions de probabilité, de génération de nombres pseudo-aléatoires, de réalisation de tests ou d’ajustement de modèles.

1 Statistiques descriptives

Les fonctions permettant de calculer des statistiques descriptives en R sont très nombreuses. Les principales sont présentées ici, mais il en existe d’autres. Le tableau suivant classe les fonctions mentionnées ci-dessous selon le type de mesure calculée (mesure de position, de tendance centrale, de dispersion ou de fréquences) et selon le type de fonctionnement de la fonction (calcul vectoriel, données combinées en une ou plusieurs valeurs).

Calcul	opère de façon vectorielle	combine, retourne une valeur	combine, retourne valeur(s)	combine, retourne un vecteur
mesure de position	`pmin`, `pmax`	`min`, `max`, `which.min`, `which.max`	`range`, `quantile`, `summary`	`cummin`, `cummax`, `rank`
tendance centrale		`mean`, `median`	`summary`
dispersion		`sd`, `IQR`, `mad`	`var`, `cov`, `cor`
fréquences			`table`, `ftable`, `xtabs`, `summary`

1.1 Fonctions retournant une seule statistique

Certaines fonctions de calcul de statistiques descriptives retournent en sortie une seule valeur. C’est le cas des fonctions suivantes :

mesures de position : min, max;
mesures de tendance centrale : mean, median;
mesure de dispersion : sd (écart-type), IQR (écart interquartile), mad (écart absolu médian).

Utilisons le jeu de données cars du package datasets pour présenter quelques exemples. Ce jeu de données contient 50 observations de 2 variables numériques.

str(cars)

## 'data.frame':    50 obs. of  2 variables:
##  $ speed: num  4 4 7 7 8 9 10 10 10 11 ...
##  $ dist : num  2 10 4 22 16 10 18 26 34 17 ...

# Moyenne des observations de la variable dist
mean(cars$dist)

## [1] 42.98

Si l’objet en entrée a plus d’une dimension, la sortie est tout de même de longueur 1. Donc tous les éléments contenus dans l’objet sont mis en commun pour faire le calcul.

max(cars)

## [1] 120

Fonctions `which.max` et `which.min`

Les fonctions min et max retournent respectivement la valeur la plus petite et la valeur la plus grande parmi les éléments d’un objet. Les fonctions which.max et which.min retournent pour leur part la position dans l’objet du premier maximum ou minimum.

which.min(cars$speed)

## [1] 1

Dans l’exemple précédent, il y a en fait deux observations qui prennent la valeur minimum de min(cars$speed). La commande suivante permet de trouver la position de toutes les observations prenant la valeur minimale.

which(cars$speed == min(cars$speed))

## [1] 1 2

1.1.1 Traitement des données manquantes et argument `na.rm`

Les fonctions min, max, mean, median et sd, ainsi que quelques autres fonctions vues dans ces notes, ont un argument en commun nommé na.rm. Cet argument sert à indiquer à la fonction comment agir en présence de données manquantes (NA). Par défaut, na.rm prend la valeur FALSE pour ces fonctions. Cette valeur signifie que les données manquantes ne doivent pas être retirées avant d’effectuer le calcul. Cependant, en présence de données manquantes, ces fonctions ne sont pas en mesure de calculer des statistiques. Par exemple, supposons que nous voulions calculer la médiane des données dans le vecteur suivant.

x <- c(3, 6, NA, 8, 11, 15, 23)

Si nous ne retirons pas la donnée manquante, nous obtenons le résultat suivant.

median(x)

## [1] NA

Ce résultat s’explique par le fait que la valeur de la médiane dépend de toutes les observations, incluant l’observation manquante, qui est inconnue. La valeur de la médiane est donc elle aussi inconnue. Pour calculer plutôt la médiane des observations non manquantes, il faut donner la valeur TRUE à l’argument na.rm comme suit.

median(x, na.rm = TRUE)

## [1] 9.5

Notons que la fonction na.omit permet de retirer les observations manquantes d’un objet R. Si l’objet est un vecteur, les éléments contenant NA sont retirés.

na.omit(x)

## [1]  3  6  8 11 15 23
## attr(,"na.action")
## [1] 3
## attr(,"class")
## [1] "omit"

La fonction na.omit ajoute deux attributs à l’objet, dont un pour identifier les observations retirées.

Remarquons que les deux commandes suivantes retournent le même résultat.

median(x, na.rm = TRUE)

## [1] 9.5

median(na.omit(x))

## [1] 9.5

Si la fonction na.omit reçoit en entrée une matrice ou un data frame, elle retire toutes les lignes contenant au moins un NA, comme dans cet exemple :

ex_jeu <- data.frame(x, y = c(2, NA, 8, 9, 6, NA, 2)); 
ex_jeu

##    x  y
## 1  3  2
## 2  6 NA
## 3 NA  8
## 4  8  9
## 5 11  6
## 6 15 NA
## 7 23  2

na.omit(ex_jeu)

##    x y
## 1  3 2
## 4  8 9
## 5 11 6
## 7 23 2

1.2 Fonctions pouvant retourner plusieurs statistiques

D’autres fonctions peuvent retourner plus d’une statistique, notamment les fonctions suivantes :

mesures de position : range, quantile;
résumé comprenant plusieurs mesures : summary;
variances, covariances et corrélations : var, cov, cor.

Fonctions `range` et `quantile`

La fonction range retourne à la fois le minimum est le maximum, comme dans cet exemple :

range(cars$speed)

## [1]  4 25

Une façon simple d’obtenir l’étendue d’observations à partir de la sortie de la fonction range est de procéder comme suit :

diff(range(cars$speed))

## [1] 21

La fonction quantile calcule des quantiles empiriques. Par défaut, elle retourne le minimum, le maximum et les quartiles, comme dans cet exemple :

quantile(cars$speed)

##   0%  25%  50%  75% 100% 
##    4   12   15   19   25

L’argument probs permet de demander n’importe quels quantiles. Dans l’exemple suivant, les premiers et neuvièmes déciles sont demandés.

quantile(cars$speed, probs = c(0.1, 0.9))

##  10%  90% 
##  8.9 23.1

Remarque : Il existe plusieurs façons de calculer des quantiles. La fonction quantile implémente 9 algorithmes de calcul de quantiles (voir help(quantile)).

Fonction `summary`

La fonction summary retourne les statistiques suivantes selon l’entrée qu’elle reçoit :

vecteur numérique : minimum, premier quartile, médiane, moyenne, troisième quartile, maximum;
facteur : fréquences des modalités (comme la fonction table vue plus loin);
matrice ou data frame : la fonction summary est appliquée séparément à chacune des colonnes.

Utilisons le jeu de données Puromycin du package datasets pour présenter quelques exemples d’utilisation de la fonction summary. Ce jeu de données contient 23 observations de 3 variables, dont deux numériques et une catégorique, stockée sous forme de facteur.

str(Puromycin)

## 'data.frame':    23 obs. of  3 variables:
##  $ conc : num  0.02 0.02 0.06 0.06 0.11 0.11 0.22 0.22 0.56 0.56 ...
##  $ rate : num  76 47 97 107 123 139 159 152 191 201 ...
##  $ state: Factor w/ 2 levels "treated","untreated": 1 1 1 1 1 1 1 1 1 1 ...
##  - attr(*, "reference")= chr "A1.3, p. 269"

# Vecteur numérique en entrée :
summary(Puromycin$rate)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    47.0    91.5   124.0   126.8   158.5   207.0

# Facteur en entrée :
summary(Puromycin$state)

##   treated untreated 
##        12        11

# Data frame entier en entrée :
summary(Puromycin)

##       conc             rate             state   
##  Min.   :0.0200   Min.   : 47.0   treated  :12  
##  1st Qu.:0.0600   1st Qu.: 91.5   untreated:11  
##  Median :0.1100   Median :124.0                 
##  Mean   :0.3122   Mean   :126.8                 
##  3rd Qu.:0.5600   3rd Qu.:158.5                 
##  Max.   :1.1000   Max.   :207.0

Fonctions `var`, `cov` et `cor`

La fonction var peut prendre en entrée un vecteur ou un objet à deux dimensions. Si elle reçoit en entrée un vecteur, elle calcule la variance empirique de toutes les valeurs, comme dans cet exemple :

var(cars$speed)

## [1] 27.95918

Cependant, si elle reçoit en entrée une matrice ou un data frame de valeurs numériques, elle considère que chaque colonne contient les observations d’une variable aléatoire. Elle va calculer une matrice de variances-covariances, comme dans cet exemple :

var(cars)

##           speed     dist
## speed  27.95918 109.9469
## dist  109.94694 664.0608

La fonction cov fait exactement le même calcul par défaut.

cov(cars)

##           speed     dist
## speed  27.95918 109.9469
## dist  109.94694 664.0608

Elle peut cependant calculer des covariances de Kendall ou de Spearman (toutes deux des statistiques non paramétriques basées sur les rangs des observations) au lieu de la covariance classique de Pearson. La fonction cor calcule des corrélations plutôt que des covariances. Elle aussi peut utiliser les définitions de Pearson (par défaut), Kendall et Spearman. Voici un exemple de calcul de matrice de corrélations de Spearman.

cor(cars, method = "spearman")

##           speed      dist
## speed 1.0000000 0.8303568
## dist  0.8303568 1.0000000

1.3 Fonctions retournant un vecteur de statistiques

Certaines fonctions, telles que les suivantes, retournent autant de statistiques qu’il y a d’éléments dans l’objet donné en entrée.

mesures de position : cummin, cummax, pmin, pmax;
rangs : rank.

Fonctions `cummin` et `cummax`

Les fonctions cummin et cummax calculent les minimums et les maximums cumulatifs. Comme nous pouvons le constater dans l’exemple suivant, la valeur en position i du vecteur retourné par une de ces deux fonctions est la valeur minimale ou maximale dans le sous-vecteur x[1:i].

cummin(x = c(-2, 4, -3, 4, 7, -6, 0))

## [1] -2 -2 -3 -3 -3 -6 -6

Fonctions `pmin` et `pmax`

Les fonctions pmin et pmax calculent le minimum et le maximum par position, entre autant de vecteurs que désiré, comme dans l’exemple suivant.

pmax(
  c(-2, 4, -3, 4, 7, -6, 0), 
  c( 1, 2,  3, 4, 5,  6, 7),
  c( 5, 0, -2, 4, 5,  3, 3)
)

## [1] 5 4 3 4 7 6 7

Ces fonctions sont utiles pour remplacer des valeurs par un seuil. Par exemple, l’instruction suivante permet de remplacer par zéro toute valeur négative contenue dans le vecteur en entrée.

pmax(c(-2, 4, -3, 4, 7, -6, 0), 0)

## [1] 0 4 0 4 7 0 0

Fonction `rank`

Certains tests statistiques non paramétriques utilisent des statistiques basées sur les rangs des observations. Voici un exemple d’obtention de ces rangs avec la fonction rank.

rank(c(-2, 4, -3, 4, 7, -6, 0))

## [1] 3.0 5.5 2.0 5.5 7.0 1.0 4.0

Par défaut, en cas d’égalité, le rang moyen est utilisé. Pour changer cette option, il faut modifier la valeur de l’argument ties.method. Dans l’exemple suivant, le rang minimum est retourné en cas d’égalité.

rank(c(-2, 4, -3, 4, 7, -6, 0), ties.method = "min")

## [1] 3 5 2 5 7 1 4

1.4 Calcul de fréquences

Les fonctions table, xtabs et ftable permettent de calculer des fréquences.

Voici un petit jeu de données pour illustrer l’utilisation de ces fonctions. Il contient des observations concernant 7 individus fictifs : la couleur de leurs yeux, la couleur de leurs cheveux et leur genre.

sondage <- data.frame(
  yeux    = c("brun",    "brun",     "bleu",    "brun",    "vert",     "brun",    "bleu"    ),
  cheveux = c("brun",    "noir",     "blond",   "brun",    "brun",     "blond",   "brun"    ),
  genre   = c("féminin", "masculin", "féminin", "féminin", "masculin", "féminin", "masculin")
)
sondage

##   yeux cheveux    genre
## 1 brun    brun  féminin
## 2 brun    noir masculin
## 3 bleu   blond  féminin
## 4 brun    brun  féminin
## 5 vert    brun masculin
## 6 brun   blond  féminin
## 7 bleu    brun masculin

Fonctions `table`

La fonction table permet de compter le nombre d’occurrences de chacune des modalités d’une variable catégorique dans des données. Demandons, par exemple, à table de compter le nombre d’individus dans les données sondage classés dans chacune des catégories de couleurs de cheveux.

table(sondage$cheveux)

## 
## blond  brun  noir 
##     2     4     1

La fonction table produit un tableau de fréquences à une variable si elle reçoit les observations d’une seule variable. Elle peut aussi produire des tableaux de fréquences croisées à deux variables ou plus.

# Exemple de tableau de fréquences à deux variables (avec variables nommées)
table(yeux = sondage$yeux, cheveux = sondage$cheveux)

##       cheveux
## yeux   blond brun noir
##   bleu     1    1    0
##   brun     1    2    1
##   vert     0    1    0

# Exemple de tableau de fréquences à trois variables (data frame en entrée à table)
t3 <- table(sondage)
t3

## , , genre = féminin
## 
##       cheveux
## yeux   blond brun noir
##   bleu     1    0    0
##   brun     1    2    0
##   vert     0    0    0
## 
## , , genre = masculin
## 
##       cheveux
## yeux   blond brun noir
##   bleu     0    1    0
##   brun     0    0    1
##   vert     0    1    0

Fonctions `ftable`

La fonction ftable retourne un tableau de fréquences sous la forme d’une table « plate » (en anglais flat, d’où le f dans le nom de la fonction) dans le cas d’un croisement de 3 variables ou plus, plutôt que sous la forme d’un array comme le fait la fonction table. Elle accepte les mêmes types d’entrées que table (série d’objets atomiques à une dimension ou objet récursif dont les éléments sont interprétables en facteurs) et peut aussi recevoir une sortie de la fonction table, comme dans l’exemple suivant.

ftable(t3)

##              genre féminin masculin
## yeux cheveux                       
## bleu blond               1        0
##      brun                0        1
##      noir                0        0
## brun blond               1        0
##      brun                2        0
##      noir                0        1
## vert blond               0        0
##      brun                0        1
##      noir                0        0

Fonctions `xtabs`

La fonction xtabs fait le même calcul que les fonctions précédentes, mais elle prend en entrée une formule. Le tableau de fréquences à deux variables créé précédemment peut être réobtenu de la façon suivante avec xtabs.

xtabs(~ yeux + cheveux, data = sondage)

##       cheveux
## yeux   blond brun noir
##   bleu     1    1    0
##   brun     1    2    1
##   vert     0    1    0

La fonction xtabs est utile lorsque les données que nous avons en main contiennent déjà des fréquences, car il est possible d’inclure une variable réponse contenant des dénombrements dans la formule que nous lui fournissons en entrée. Par exemple, xtabs permet de facilement retrouver le tableau de fréquences marginales croisées entre les variables yeux et cheveux à partir du tableau de fréquences à trois variables produit précédemment mis sous forme de data frame, qui a l’allure suivante.

t3_df <- as.data.frame(t3)
t3_df

##    yeux cheveux    genre Freq
## 1  bleu   blond  féminin    1
## 2  brun   blond  féminin    1
## 3  vert   blond  féminin    0
## 4  bleu    brun  féminin    0
## 5  brun    brun  féminin    2
## 6  vert    brun  féminin    0
## 7  bleu    noir  féminin    0
## 8  brun    noir  féminin    0
## 9  vert    noir  féminin    0
## 10 bleu   blond masculin    0
## 11 brun   blond masculin    0
## 12 vert   blond masculin    0
## 13 bleu    brun masculin    1
## 14 brun    brun masculin    0
## 15 vert    brun masculin    1
## 16 bleu    noir masculin    0
## 17 brun    noir masculin    1
## 18 vert    noir masculin    0

Il suffit de procéder comme suit :

t2 <- xtabs(Freq ~ yeux + cheveux, data = t3_df)
t2

##       cheveux
## yeux   blond brun noir
##   bleu     1    1    0
##   brun     1    2    1
##   vert     0    1    0

Autres fonctions relatives au calcul de fréquences

Les fonctions marginSums, addmargins et proportions permettent de calculer des fréquences marginales ou relatives à partir d’un tableau de fréquences. Voici quelques exemples d’utilisation de ces fonctions exploitant le tableau de fréquences à deux variables produit ci-dessus.

# Fréquences marginales en colonnes :
marginSums(t2, margin = 2)

## cheveux
## blond  brun  noir 
##     2     4     1

# Fréquences marginales ajoutées au tableau :
addmargins(t2)

##       cheveux
## yeux   blond brun noir Sum
##   bleu     1    1    0   2
##   brun     1    2    1   4
##   vert     0    1    0   1
##   Sum      2    4    1   7

# Fréquences relatives croisées :
proportions(t2)

##       cheveux
## yeux       blond      brun      noir
##   bleu 0.1428571 0.1428571 0.0000000
##   brun 0.1428571 0.2857143 0.1428571
##   vert 0.0000000 0.1428571 0.0000000

# Fréquences relatives conditionnelles à la variable yeux :
proportions(t2, margin = 1)

##       cheveux
## yeux   blond brun noir
##   bleu  0.50 0.50 0.00
##   brun  0.25 0.50 0.25
##   vert  0.00 1.00 0.00

Transformation du format d’un objet de classe `"table"`

Les fonctions table et xtabs attribuent à l’objet qu’ils retournent en sortie la classe "table", comme nous pouvons le constater en observant l’objet t2.

attributes(t2)

## $dim
## [1] 3 3
## 
## $dimnames
## $dimnames$yeux
## [1] "bleu" "brun" "vert"
## 
## $dimnames$cheveux
## [1] "blond" "brun"  "noir" 
## 
## 
## $class
## [1] "xtabs" "table"
## 
## $call
## xtabs(formula = Freq ~ yeux + cheveux, data = t3_df)

str(t2)

##  'xtabs' int [1:3, 1:3] 1 1 0 1 2 1 0 1 0
##  - attr(*, "dimnames")=List of 2
##   ..$ yeux   : chr [1:3] "bleu" "brun" "vert"
##   ..$ cheveux: chr [1:3] "blond" "brun" "noir"
##  - attr(*, "call")= language xtabs(formula = Freq ~ yeux + cheveux, data = t3_df)

Il est parfois utile de transformer un objet de classe "table" en un array (matrice si la table croise deux variables) ou un data frame. Pour la transformation en array, il suffit de retirer l’attribut class avec la fonction unclass, comme dans cet exemple :

str(unclass(t2))

##  int [1:3, 1:3] 1 1 0 1 2 1 0 1 0
##  - attr(*, "dimnames")=List of 2
##   ..$ yeux   : chr [1:3] "bleu" "brun" "vert"
##   ..$ cheveux: chr [1:3] "blond" "brun" "noir"
##  - attr(*, "call")= language xtabs(formula = Freq ~ yeux + cheveux, data = t3_df)

Comme nous avons pu le constater dans un exemple précédent, la transformation en data frame crée pour sa part un jeu de données contenant une ligne par combinaison distincte des niveaux des facteurs croisés dans la table. Le data frame obtenu comporte une colonne par facteur, ainsi qu’une colonne nommée Freq contenant les fréquences dans la table. En voici un exemple :

str(as.data.frame(t2))

## 'data.frame':    9 obs. of  3 variables:
##  $ yeux   : Factor w/ 3 levels "bleu","brun",..: 1 2 3 1 2 3 1 2 3
##  $ cheveux: Factor w/ 3 levels "blond","brun",..: 1 1 1 2 2 2 3 3 3
##  $ Freq   : int  1 1 0 1 2 1 0 1 0

1.5 Énumération de combinaisons

Un fonction utile pour énumérer toutes les combinaisons des niveaux d’un facteur est expand.grid. Par exemple, retrouvons avec cette fonction toutes les combinaisons présentes dans le data frame t3_df créé précédemment.

expand.grid(
  yeux = c("bleu", "brun", "vert"),
  cheveux = c("blond", "brun", "noir"),
  genre = c("féminin", "masculin")
)

##    yeux cheveux    genre
## 1  bleu   blond  féminin
## 2  brun   blond  féminin
## 3  vert   blond  féminin
## 4  bleu    brun  féminin
## 5  brun    brun  féminin
## 6  vert    brun  féminin
## 7  bleu    noir  féminin
## 8  brun    noir  féminin
## 9  vert    noir  féminin
## 10 bleu   blond masculin
## 11 brun   blond masculin
## 12 vert   blond masculin
## 13 bleu    brun masculin
## 14 brun    brun masculin
## 15 vert    brun masculin
## 16 bleu    noir masculin
## 17 brun    noir masculin
## 18 vert    noir masculin

Il faut fournir en entrée à expand.grid les valeurs à combiner. Si les vecteurs ou facteurs contenant ces valeurs sont fournis avec des noms, comme dans l’exemple précédent (via les assignations), les colonnes du data frame retourné en sortie par expand.grid porteront ces noms.

Une autre fonction R permet d’énumérer des combinaisons possibles : la fonction combn. Il s’agit de combinaisons au sens mathématique cette fois, donc « de dispositions non ordonnées d’un certain nombre d’éléments d’un ensemble » (définition tirée du site web alloprof). Par exemple, voici toutes les combinaisons possibles de 3 éléments parmi l’ensemble c("Ève", "Jean", "Mia", "Paul"), trouvées par la fonction combn.

combn(x = c("Ève", "Jean", "Mia", "Paul"), m = 3)

##      [,1]   [,2]   [,3]   [,4]  
## [1,] "Ève"  "Ève"  "Ève"  "Jean"
## [2,] "Jean" "Jean" "Mia"  "Mia" 
## [3,] "Mia"  "Paul" "Paul" "Paul"

Contrairement à expand.grid qui présente les combinaisons possibles ligne par ligne, chaque colonne de la sortie produite par combn représente une combinaison possible.

Notons finalement que la fonction choose mentionnée précédemment permet de compter le nombre de combinaisons possibles de k éléments d’un ensemble de taille n. Elle calcule donc le coefficient binomial ${n\choose k}$.

# Nombre de combinaisons possibles dans l'exemple précédent :
choose(n = 4, k = 3)

## [1] 4

2 Distributions de probabilité

Le package stats de l’installation de base de R comprend, pour plusieurs distributions de probabilité, des fonctions de calcul de :

la fonction de densité (forme d* où * change selon la distribution),
la fonction de répartition (forme p*) et
la fonction quantile (forme q*).

La fiche d’aide ouverte par la commande help(Distributions) énumère toutes les distributions de probabilité offertes dans le package stats. Il existe aussi des fonctions relatives à d’autres distributions de probabilité dans des packages sur le CRAN (voir https://CRAN.R-project.org/view=Distributions pour découvrir ce qui est offert).

Ces fonctions sont utiles notamment pour calculer des valeurs critiques ou des seuils observés de tests d’hypothèses. Un exemple est présenté plus loin.

2.1 Fonction de densité

Les fonctions R implémentant des fonctions de densité ont un nom qui débute par le lettre d pour density. Leur premier argument est toujours un vecteur de valeurs en lesquelles calculer la fonction de densité. Les arguments suivants servent à spécifier les valeurs des paramètres de la distribution.

Dans le cas d’une variable aléatoire discrète, la fonction de densité est plus justement appelée fonction de masse. Il s’agit alors d’une probabilité, pour une variable aléatoire suivant une certaine distribution, de prendre une certaine valeur.

Exemple : distribution binomiale

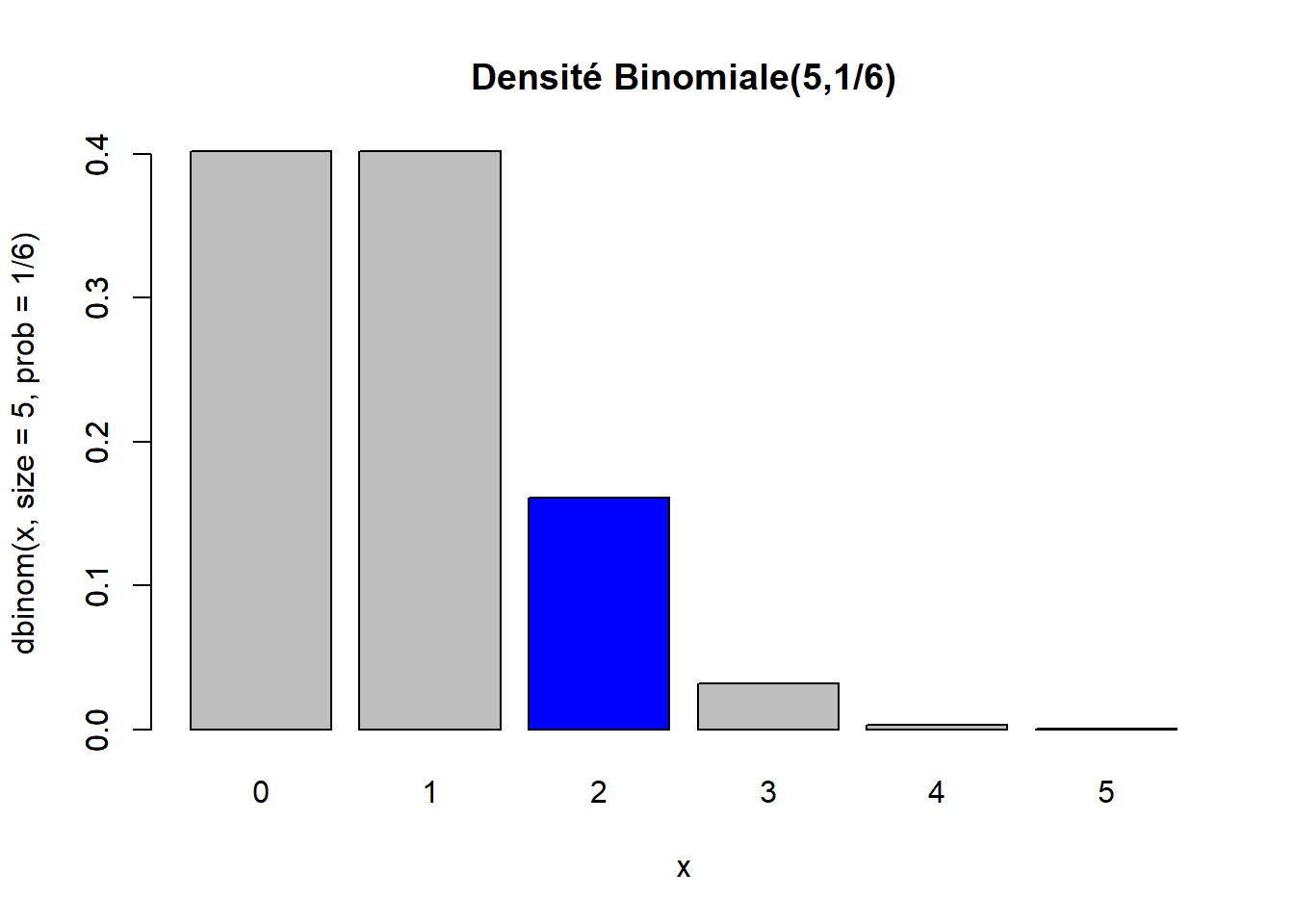
Soit $X$ une variable aléatoire représentant le nombre de 6 obtenus lors de 5 lancés d’un dé. Cette variable aléatoire suit une distribution binomiale de paramètres $n = 5$ et $p = 1/6$, donc $X \sim Bin(n = 5, p = 1/6)$.

Calculons $P(X = 2)$, soit la probabilité que la variable aléatoire $X$ prenne la valeur 2.

dbinom(x = 2, size = 5, prob = 1/6)

## [1] 0.160751

La fonction dbinom implémente donc la fonction de masse d’une distribution binomiale. Les arguments size et prob sont les paramètres $n$ et $p$ de la distribution, selon la notation utilisée ci-dessus.

Les fonctions de la famille d* peuvent calculer plusieurs valeurs de densité par un seul appel de la fonction, car celles-ci acceptent des valeurs d’arguments de longueur supérieure à 1. Ces fonctions travaillent donc de façon vectorielle, comme presque toutes les fonctions de calcul en R.

Voici un exemple de code R permettant de représenter graphiquement la densité $Bin(n = 5, p = 1/6)$ complète, en mettant en évidence la valeur calculée ci-dessus, soit $P(X = 2)$. (Nous verrons dans les notes sur les graphiques comment produire ce genre de figure et les suivantes.)

barplot(
  height = dbinom(0:5, size = 5, prob = 1/6), 
  names.arg = 0:5,
  main = "Densité Binomiale(5,1/6)",
  xlab = "x",
  ylab = "dbinom(x, size = 5, prob = 1/6)"
)
barplot(
  height = c(0, 0, dbinom(2, size = 5, prob = 1/6), 0, 0, 0),
  col = "blue",
  add = TRUE
)

Exemple : distribution normale standard

Supposons maintenant que $X$ est une variable aléatoire continue de distribution normale standard, donc $X \sim N(\mu = 0, \sigma^2 = 1)$. La valeur de la fonction de densité pour cette distribution en la valeur $x = 1$, souvent notée $f_X(1)$, vaut :

dnorm(x = 1)

## [1] 0.2419707

Voici une représentation graphique de la densité complète dans laquelle la valeur calculée ci-dessus est mise en évidence.

curve(expr = dnorm, xlim = c(-3, 3), main = "Densité N(0,1)")
segments(
  x0 = c(-4, 1), y0 = dnorm(1), x1 = 1, y1 = c(dnorm(1), -1), 
  lty = 2, col = "blue"
)

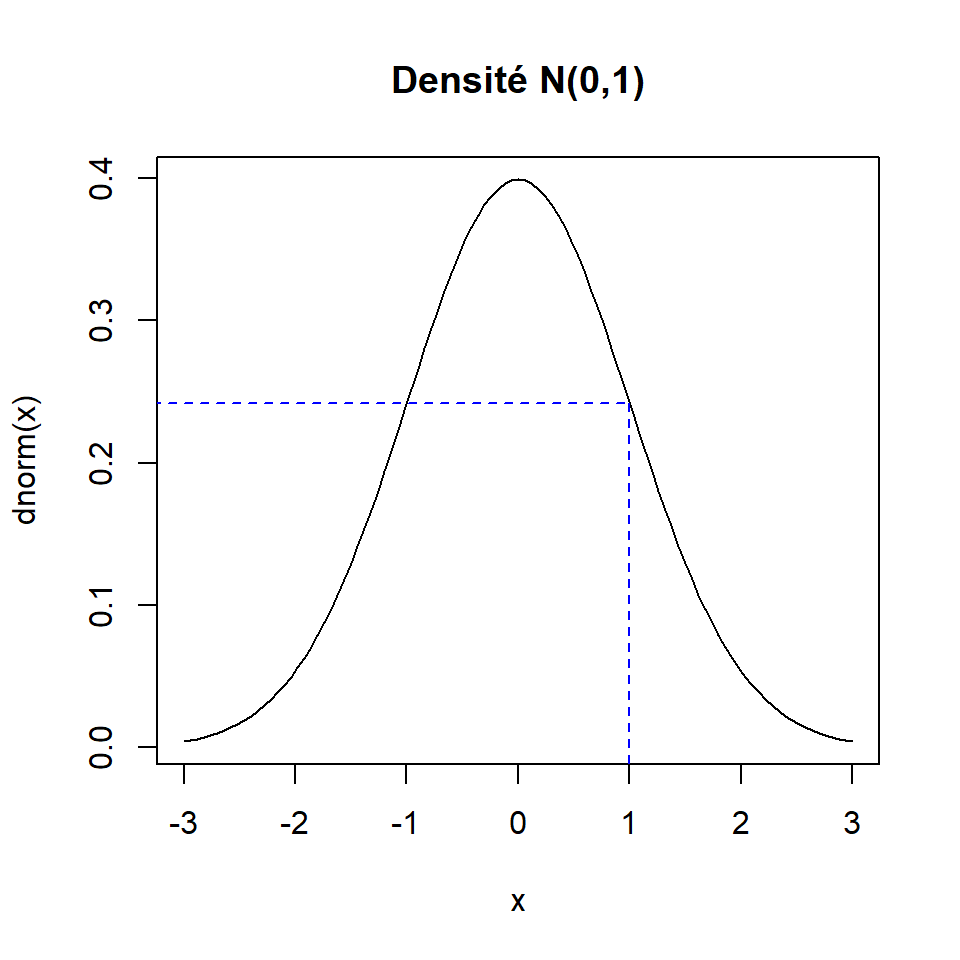
Ici, nous n’avons pas eu besoin de fournir des valeurs aux arguments de la fonction dnorm relatifs aux paramètres de la distribution, parce que nous avons utilisés leurs valeurs par défaut. Ces paramètres, pour la densité $N(\mu, \sigma^2)$, sont représentés par les arguments mean = $\mu$ et sd = $\sigma$ (remarquez que l’argument de la fonction R représente l’écart-type, pas la variance).

Tout comme le premier argument, nommé $x$, les arguments des fonctions de la famille d* représentant des paramètres de la distribution acceptent aussi en entrée plus d’une valeur. Voici un exemple, qui permet de calculer la densité en $x = 1$ pour $X \sim N(\mu = -2, \sigma^2 = 1)$, $X \sim N(\mu = 0, \sigma^2 = 2.25)$ et $X \sim N(\mu = 1, \sigma^2 = 4)$ en un seul appel à la fonction dnorm.

dnorm(x = 1, mean = c(-2, 0, 1), sd = c(1, 1.5, 2))

## [1] 0.004431848 0.212965337 0.199471140

2.2 Fonction de répartition

La fonction de répartition d’une variable aléatoire $X$ est définie par $F_X(x) = P(X \le x)$. Il s’agit donc toujours d’une probabilité, d’où le p au début des noms des fonctions R implémentant des fonctions de répartition.

Exemple : distribution normale standard

Prenons encore comme exemple la distribution normale standard. Nous avons donc $X \sim N(0, 1)$. Calculons la valeur de la fonction de répartition de cette variable aléatoire en $x = 1$.

pnorm(q = 1)

## [1] 0.8413447

Il s’agit de la valeur de la probabilité $P(X \le 1)$.

Le premier argument des fonctions de la famille p* ne se nomme pas x, il se nomme plutôt q. Cette lettre réfère au mot quantile et souligne le lien entre les fonctions de répartition et les fonctions quantiles. Les arguments suivants des fonctions de la famille p* permettent de spécifier les valeurs des paramètres de la distribution, comme pour les fonctions de la famille p*.

Voici une illustration graphique du lien entre la fonction de densité et la fonction de répartition en utilisant la distribution normale standard. La valeur de la fonction de répartition en un point quelconque $x$ (dans le graphique $x = 1$) est égale à l’aire sous la courbe de densité entre $-\infty$ et $x$.

par_default <- par(mfrow = c(1, 2))

curve(expr = dnorm, xlim = c(-3, 3), main = "Densité N(0,1)")
x <- seq(from = -3, to = 1, length = 100)
polygon(x = c(x, 1, -3), y = c(dnorm(x), 0, 0), col = "blue")

curve(
  expr = pnorm, xlim = c(-3, 3), 
  main = "Fonction de répartition N(0,1)", xname = "q"
)
segments(
  x0 = c(-4, 1), y0 = pnorm(1), x1 = 1, y1 = c(pnorm(1), -1), 
  lty = 2, col = "blue"
)

par(par_default)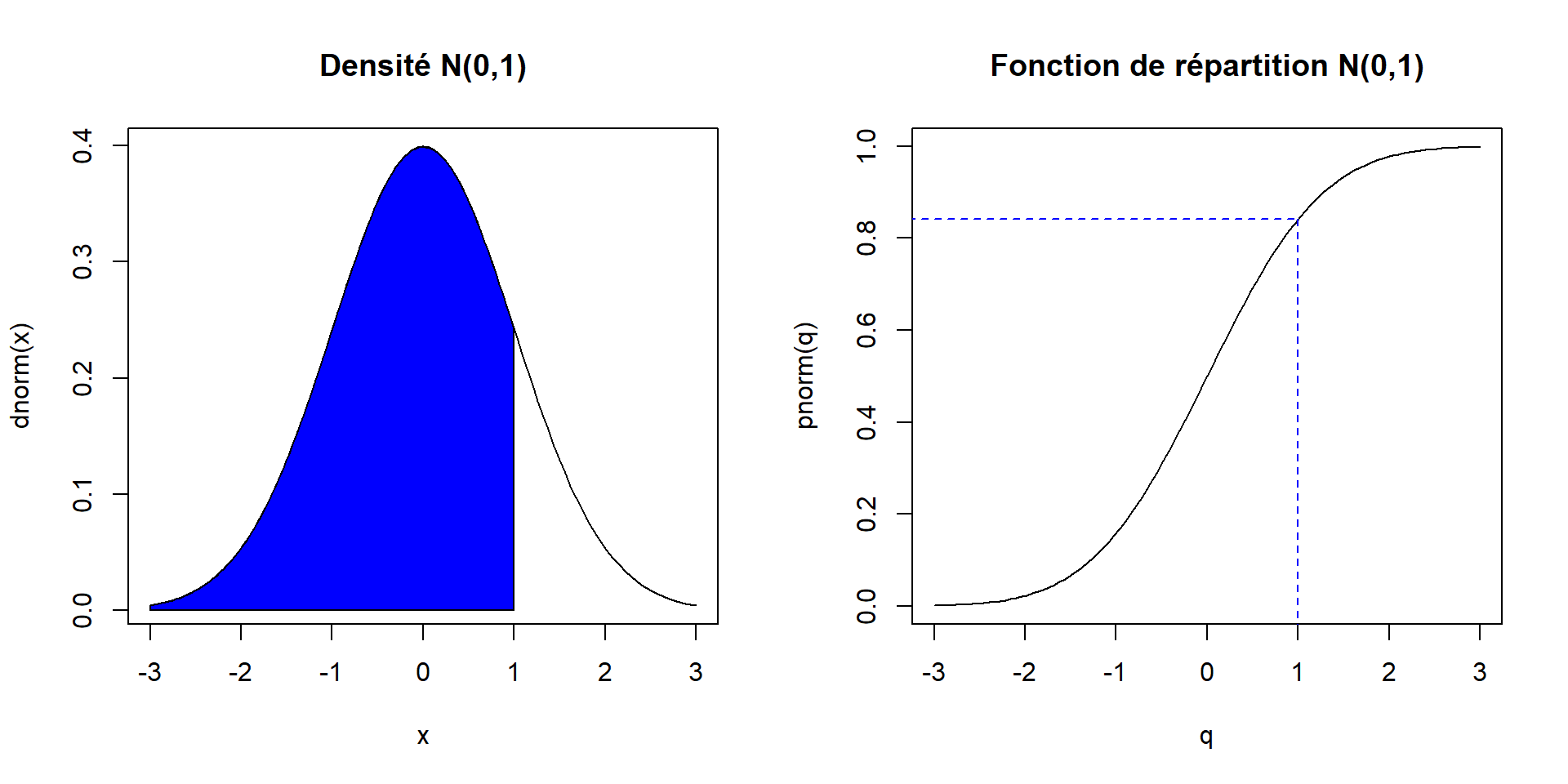

2.3 Fonction quantile

La fonction quantile est l’inverse généralisé de la fonction de répartition. Les fonctions R implémentant des fonctions quantile ont un nom qui débute par le lettre q pour quantile.

Exemple : distribution normale standard

Pour clore l’exemple de la distribution normale standard, voyons de quoi à l’air la fonction quantile de cette distribution.

Premièrement, calculons la valeur de la fonction quantile en un point, disons en $p = 0.8413447$.

qnorm(p = 0.8413447)

## [1] 0.9999998

Il s’agit de la valeur $x$ pour laquelle $P(X \le x) = 0.8413447$, où $X \sim N(0, 1)$.

Le premier argument d’une fonction de la famille q* se nomme p. Cette notation peut nous aider à nous rappeler que cet argument représente une probabilité et accepte donc seulement des valeurs entre 0 et 1. Encore une fois, les arguments suivants des fonctions de la famille q* permettent de spécifier les valeurs des paramètres de la distribution.

Le graphique suivant illustre le lien entre la fonction de répartition et la fonction quantile. Le graphique de la fonction quantile est simplement obtenu en inversant les axes du graphique de la fonction de répartition.

par_default <- par(mfrow = c(1,2), pty = "s")

curve(
  expr = pnorm, xlim = c(-3, 3), n = 1000, ylim = c(0, 1), asp = 6,
  main = "Fonction de répartition N(0,1)", xname = "q"
)
segments(
  x0 = c(-4, 1), y0 = pnorm(1),  x1 = 1, y1 = c(pnorm(1), -1), 
  lty = 2, col = "blue"
)

curve(
  expr = qnorm, xlim = c(0, 1), n = 1000, ylim = c(-3, 3), asp = 1/6, 
  main = "Fonction quantile  N(0,1)", xname = "p"
)
segments(
  x0 = c(-0.2, pnorm(1)), y0 = qnorm(pnorm(1)), 
  x1 = pnorm(1), y1 = c(qnorm(pnorm(1)), -4), 
  lty = 2, col = "blue"
)

par(par_default)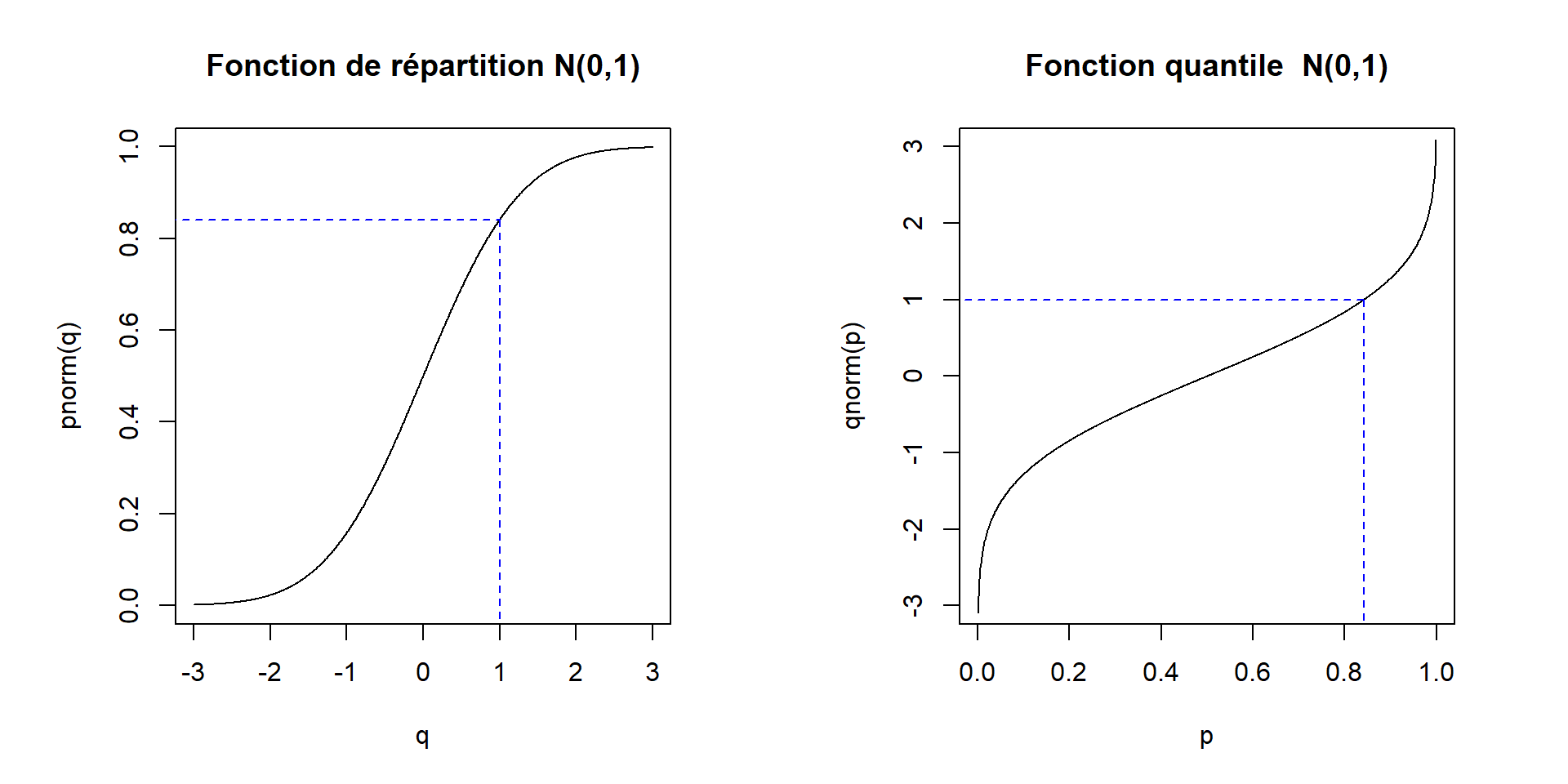

3 Génération de nombres pseudo-aléatoires

En R, les fonctions r* permettent de générer pseudo-aléatoirement des observations selon une certaine distribution désignée par *. La lettre r au début de leur nom signifie random.

Par exemple, voici la représentation graphique de 3 échantillons générés aléatoirement selon 3 distributions différentes : des distributions normale, uniforme continue et khi-deux. Pour chaque échantillon, nous traçons l’histogramme des observations simulées pour représenter leur densité empirique. Nous superposons à cet histogramme la courbe de densité de la distribution théorique à partir de laquelle les observations ont été générées.

par_default <- par(mfrow = c(1, 3))

# Densité normale d'espérance 5 et de variance 4
x1 <- rnorm(1000, mean = 5, sd = 2)
hist(x = x1, freq = FALSE, ylab = "Proportion", main = "Densité empirique de x1")
curve(expr = dnorm(x, mean = 5, sd = 2), add = TRUE, col = "blue")
title(main = "courbe bleue = densité visée N(5,4)", line = 0.5)

# Densité uniforme continue entre 2 et 8
x2 <- runif(1000, min = 2, max = 8)
hist(x = x2, freq = FALSE, ylab = "Proportion", main = "Densité empirique de x2")
curve(expr = dunif(x, min = 2, max = 8), add = TRUE, col = "blue")
title(main = "courbe bleue = densité visée U(2,8)", line = 0.5)

# Densité chi-carré à 4 degrés de liberté
x3 <- rchisq(1000, df = 4)
hist(x = x3, freq = FALSE, ylab = "Proportion", main = "Densité empirique de x3")
curve(expr = dchisq(x, df = 4), add = TRUE, col = "blue")
title(main = expression(paste("courbe bleue = densité visée ", chi[4]^2)), line = 0.5)

par(par_default)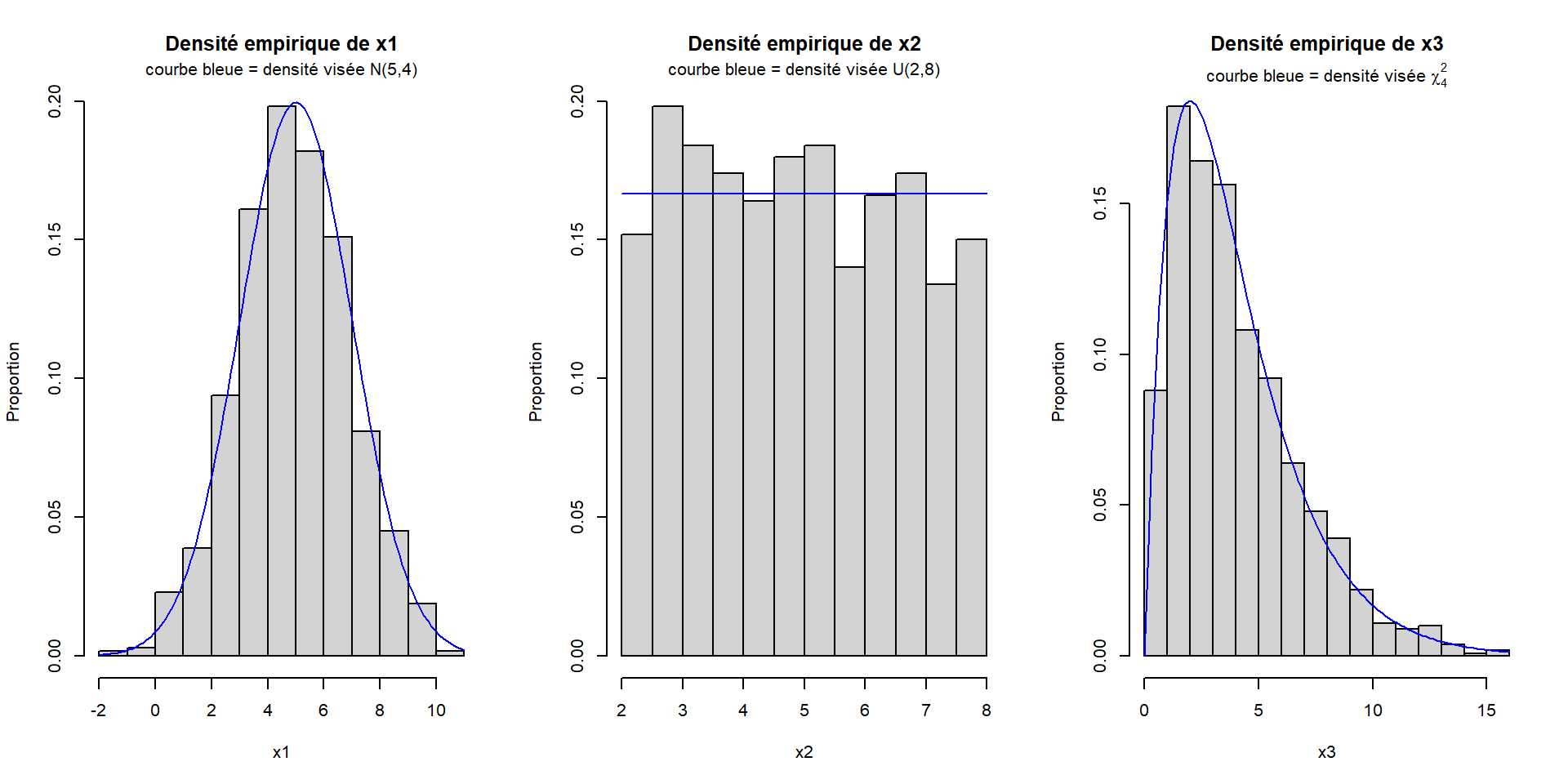

Comme nous pouvons le constater sur ces graphiques, la distribution empirique des observations générées avec ces fonctions se rapproche vraiment de la distribution théorique demandée. En générant un nombre encore plus grand d’observations (ici nous en avons généré 1000 pour chaque distribution), la densité empirique se rapprocherait encore plus de la densité théorique.

3.1 Fonction `sample`

La fonction sample permet de tirer un échantillon aléatoire parmi un ensemble d’éléments fourni à son argument x sous forme de vecteur.

sample(x = c("Luc", "Kim", "Paul", "Ève"))

## [1] "Kim"  "Luc"  "Ève"  "Paul"

Ce vecteur peut contenir des données de n’importe quel type.

sample(x = 1:6)

## [1] 1 3 2 6 5 4

Par défaut, sample effectue un tirage sans remise et sélectionne autant d’éléments que l’ensemble de départ en contient. La fonction effectue donc une permutation aléatoire des éléments de l’ensemble de départ. L’argument size permet cependant de contrôler la taille de l’échantillon tiré.

sample(x = 1:6, size = 5)

## [1] 2 4 3 5 6

L’argument replace permet quant à lui de spécifier si le tirage doit être effectué avec (replace = TRUE) ou sans remise (replace = FALSE, valeur par défaut).

sample(x = 1:6, size = 10, replace = TRUE)

##  [1] 4 2 4 3 2 2 1 5 6 1

Il est aussi possible d’attribuer des probabilité de sélection à chacun des éléments grâce à l’argument prob. Par défaut, tous les éléments ont une probabilité égale d’être tiré.

sample(x = 1:6, size = 20, replace = TRUE, prob = c(1/2, rep(1/10, times = 5)))

##  [1] 1 2 1 3 4 1 1 1 4 3 1 6 1 2 1 1 1 4 6 2

La fonction sample.int est très similaire à la fonction sample, mais elle prend comme premier argument un seul entier, n, et tire aléatoirement size entiers entre 1 et n.

sample.int(n = 6, size = 4)

## [1] 2 4 1 5

Si nous souhaitons sélectionner aléatoirement des observations (lignes) dans un jeu de données, il est d’usage de sélectionner d’abord des entiers compris entre 1 et le nombre total d’observations, puis d’extraire du jeu de donnée les observations sur les lignes portant les numéros sélectionnés. Voici un exemple, utilisant célèbres données iris, incluses dans l’installation de base de R dans le data frame nommé iris (du package datasets).

str(iris)

## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

index_ech <- sample.int(n = nrow(iris), size = 5, replace = FALSE)
index_ech

## [1] 136  18  19  69  91

iris_ech <- iris[index_ech, ]
iris_ech

##     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 136          7.7         3.0          6.1         2.3  virginica
## 18           5.1         3.5          1.4         0.3     setosa
## 19           5.7         3.8          1.7         0.3     setosa
## 69           6.2         2.2          4.5         1.5 versicolor
## 91           5.5         2.6          4.4         1.2 versicolor

3.2 Germe de la génération pseudo-aléatoire

Les nombres générés avec les fonctions r* et les échantillons tirés avec sample sont qualifiés de pseudo-aléatoires, car ils proviennent d’un algorithme déterministe qui tente de reproduire le hasard. Un tel algorithme est nommé en anglais random number generator (RNG) ou pseudo-random number generator. La fiche d’aide ouverte par la commande help(Random) contient de l’information sur la génération de nombres pseudo-aléatoires en R.

Plusieurs RNG sont implémentés en R. Celui utilisé par défaut, nommé Mersenne Twister, a été choisi parce qu’il est réputé être bon. Sans entrer dans les détails du fonctionnement des RNG implémentés dans le package base de R, il faut savoir qu’ils travaillent tous à partir d’une séquence de nombres appelée germe (en anglais seed). En contrôlant ce germe, il est possible de générer de nouveau, autant de fois que désiré, les mêmes valeurs.

Par défaut, R contrôle le germe des RNG de façon automatique. Chaque fois qu’une commande faisant intervenir un RNG est évaluée, R crée un nouveau germe à partir, notamment, de l’heure à laquelle la commande est soumise. Ainsi, deux générations pseudo-aléatoires consécutives ne produisent en général pas le même résultat.

sample(x = letters, size = 5)

## [1] "e" "k" "v" "n" "u"

sample(x = letters, size = 5)

## [1] "k" "p" "u" "o" "n"

En tout temps, il est possible de connaître le germe du RNG en R. Il est stocké dans un objet nommé .Random.seed. Cet objet est un vecteur numérique de longueur 626 pour le RNG Mersenne Twister. Voyons de quoi ont l’air les premiers éléments de ce vecteur à différents moments.

str(.Random.seed)

##  int [1:626] 10403 76 722238004 552337818 -1279533595 -1491617409 -434728698 -1712133..

sample(x = letters, size = 5)

## [1] "o" "t" "l" "z" "b"

str(.Random.seed)

##  int [1:626] 10403 82 722238004 552337818 -1279533595 -1491617409 -434728698 -1712133..

sample(x = letters, size = 5)

## [1] "z" "e" "b" "u" "a"

str(.Random.seed)

##  int [1:626] 10403 87 722238004 552337818 -1279533595 -1491617409 -434728698 -1712133..

Nous constatons qu’au moins un élément de ce vecteur (le deuxième élément) change à chaque fois que nous appelons la fonction sample. La fonction set.seed permet de fixer le germe du RNG à partir d’une seule valeur entière. Par exemple, la commande suivante :

set.seed(753)

spécifie le germe suivant :

str(.Random.seed)

##  int [1:626] 10403 624 302719261 615841082 -1828406925 -1314498536 214287161 14262109..

En soumettant de nouveau le même appel à la fonction sample, nous obtenons l’échantillon suivant.

sample(x = letters, size = 5)

## [1] "v" "r" "g" "i" "t"

La soumission de cette commande a eu pour effet de modifier le germe.

str(.Random.seed)

##  int [1:626] 10403 6 47777699 -819670847 -326033232 523235278 1163109177 1104276299 1..

Donc si nous resoumettons la commande sample, nous n’obtiendrons sûrement pas le même résultat.

sample(x = letters, size = 5)

## [1] "l" "q" "f" "e" "k"

Par contre, si nous fixons de nouveau le germe à partir de l’entier 753 avec set.seed, nous arrivons à obtenir de nouveau l’avant-dernier échantillon généré.

set.seed(753)
sample(x = letters, size = 5)

## [1] "v" "r" "g" "i" "t"

À n’importe quel moment, dans n’importe qu’elle session R, nous obtenons l’échantillon {v, r, g, i, t} si nous soumettons la commande set.seed(753) avant la commande sample(letters, size = 5).

L’utilité de fixer le germe d’une génération pseudo-aléatoire est de rendre son résultat reproductible.

4 Tests statistiques

Il existe des fonctions R pour faire des tests statistiques de base. En voici quelques-unes :

tests sur une ou des moyennes : t.test;
tests sur une ou des proportions : prop.test, binom.test;
tests de comparaison de variances : var.test, bartlett.test;
tests sur une corrélation : cor.test;
tests pour une distribution : shapiro.test, ks.test;
tests non paramétriques : wilcox.test, kruskal.test, friedman.test;
tests sur des fréquences : méthode summary pour un objet de classe table (produit par la fonction table ou xtabs), chisq.test, fisher.test, mantelhaen.test.

Utilisons encore une fois les données iris pour construire un exemple de test de comparaison de moyennes. Nous allons comparer les largeurs moyennes des sépales des espèces versicolor et virginica.

Exemple : test t bilatéral de comparaison de moyennes, avec variances inégales

t.test(
  formula = Sepal.Width ~ Species,
  data = iris,
  subset = Species %in% c("versicolor", "virginica")
)

## 
##  Welch Two Sample t-test
## 
## data:  Sepal.Width by Species
## t = -3.2058, df = 97.927, p-value = 0.001819
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.33028364 -0.07771636
## sample estimates:
## mean in group versicolor  mean in group virginica 
##                    2.770                    2.974

Lorsque nous connaissons la valeur d’une statistique de test ainsi que sa loi sous l’hypothèse nulle, il est possible de calculer en R le seuil observé du test avec la bonne fonction p*. Par exemple, dans le test t ci-dessus, nous pouvons retrouver la valeur du seuil observé ainsi :

# multiplication par 2, car le test est bilatéral et la loi t est symétrique
pt(q = -3.2058, df = 97.927)*2

## [1] 0.001819258

Exemple : test non paramétrique équivalent

wilcox.test(
  formula = Sepal.Width ~ Species,
  data = iris, 
  subset = Species %in% c("versicolor", "virginica"), 
  exact = FALSE
)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  Sepal.Width by Species
## W = 841, p-value = 0.004572
## alternative hypothesis: true location shift is not equal to 0

5 Ajustement de modèles

Il existe plusieurs fonctions en R pour ajuster des modèles. Les modèles les plus usuels sont :

modèles linéaires, dont la régression : lm pour linear model;
modèle d’analyse de la variance : lm ou aov;
modèles linéaires généralisés : glm;
modèles linéaires mixtes (peuvent contenir des effets aléatoires) : lmer du package lme4 ou lme du package nlme;
modèles non linéaires : nls.

À titre d’exemples, ajustons deux modèles sur les données iris.

Exemple : régression linéaire simple entre la largeur et la longueur des sépales

reg <- lm(formula = Sepal.Width ~ Sepal.Length, data = iris)
reg

## 
## Call:
## lm(formula = Sepal.Width ~ Sepal.Length, data = iris)
## 
## Coefficients:
##  (Intercept)  Sepal.Length  
##      3.41895      -0.06188

Exemple : ANOVA pour comparer les largeurs de sépales moyennes entre toutes les espèces

ANOVA <- aov(formula = Sepal.Width ~ Species, data = iris)
ANOVA

## Call:
##    aov(formula = Sepal.Width ~ Species, data = iris)
## 
## Terms:
##                  Species Residuals
## Sum of Squares  11.34493  16.96200
## Deg. of Freedom        2       147
## 
## Residual standard error: 0.3396877
## Estimated effects may be unbalanced

5.1 Formules

Ces fonctions d’ajustement de modèles prennent obligatoirement en entrée une formule R assignée à l’argument formula, tout comme la fonction xtabs. D’autres fonctions acceptent aussi en entrée une formule, sans que ce type d’argument soit obligatoire. C’est le cas des fonctions aggregate, ftable, plusieurs des fonctions effectuant un test (p. ex. t.test, wilcox.test) et certaines fonctions graphiques (p. ex. plot, boxplot).

Les fonctions prenant une formule en entrée ont toujours un argument data pour spécifier d’où tirer les variables incluses dans la formule.

Une formule s’écrit sous la forme y ~ x1 + x2 où y représente la variable réponse (ou à expliquer, ou dépendante, ou endogène) et x1 et x2 des variables explicatives (ou indépendantes, ou exogènes). Dans la partie de droite, les opérateurs suivants peuvent apparaître :

« + » : pour ajouter des termes;
« - » : pour soustraire des termes;
« 0 » : ou 1 pour représenter l’ordonnée à l’origine (par défaut tout modèle linéaire comporte une ordonnée à l’origine, pour la retirer il faut ajouter - 1 ou + 0 à la partie de droite de la formule);
« . » : pour représenter toutes les variables dans le jeu de données fournit en argument data, autres que la variable mise à la gauche du ~ (note : le point signifie autre chose dans la fonction update).

Opérateurs propres aux facteurs :

« : » : pour les termes d’interaction entre facteurs;
« * » : pour le croisement de facteurs (x1*x2 est équivalent à x1 + x2 + x1:x2);
« ^ » : pour le croisement de facteurs jusqu’à un certain niveau d’interaction (par exemple (x1 + x2 + x3)^2 va inclure tous les termes de croisement des facteurs jusqu’aux interactions doubles x1 + x2 + x3 + x1:x2 + x1:x3 + x2:x3, mais pas l’interaction triple x1:x2:x3);
« %in% » : pour les facteurs emboîtés (dans x2 %in% x1, x2 est emboîté dans x1).

Autre opérateur :

« | » : (p. ex. y ~ x1 | x2) n’a pas toujours exactement la même signification selon la fonction, il représente parfois :
- un conditionnement par rapport à une variable (p. ex. fonction coplot),
- la structure d’effets aléatoires (p. ex. fonctions lmer du package lme4 ou lme du package nlme).

Les formules peuvent inclurent des appels à des fonctions pour transformer les variables. Par exemple, pour ajuster un modèle sur la racine carrée de la variable réponse, nous pouvons écrire sqrt(y) ~ x1 + x2. Certaines transformations pourraient faire intervenir un ou des opérateurs ayant une signification modifiée dans la partie de droite d’une formule. Par exemple, imaginons que nous voulons ajuster un modèle avec une seule variable explicative créée en additionnant les valeurs des variables x1 et x2. La formule y ~ x1 + x2 n’ajuste pas ce modèle puisque dans la partie de droite d’une formule l’opérateur + signifie « ajouter des termes » et non plus « additionner des valeurs ». Alors est-il possible d’ajuster le modèle souhaité (sans ajouter une nouvelle variable dans les données)?

Oui, c’est possible grâce à la fonction I. Il faut encadrer l’opération arithmétique à effectuer dans la formule d’un appel à la fonction I. Par exemple, y ~ I(x1 + x2) ajuste un modèle à une seule variable explicative formée de la somme des valeurs de x1 et x2. Ainsi, I() permet d’utiliser la signification usuelle des opérateurs et non celle spécifique aux formules.

5.1.1 Exemples

Voici quelques exemples, dans lesquels nous omettrons de nommer le premier argument, soit formula, pour alléger la présentation et parce qu’il est usuel de ne pas nommer ce premier argument.

5.1.1.1 Retrait de l’ordonnée à l’origine

reg <- lm(Sepal.Width ~ Sepal.Length - 1, data = iris)
# ou encore :
reg <- lm(Sepal.Width ~ Sepal.Length + 0, data = iris)

coef(summary(reg))

##               Estimate  Std. Error  t value      Pr(>|t|)
## Sepal.Length 0.5117739 0.008939966 57.24562 2.422615e-103

5.1.1.2 Régression log-log

reg <- lm(log(Sepal.Width) ~ log(Sepal.Length), data = iris)

coef(summary(reg))

##                     Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)        1.3057236 0.14573780  8.959402 1.293792e-15
## log(Sepal.Length) -0.1129573 0.08275742 -1.364920 1.743495e-01

5.1.1.3 Régression polynomiale

reg <- lm(Sepal.Width ~ Sepal.Length + Sepal.Length^2, data = iris)

coef(summary(reg))

##                Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)   3.4189468 0.25356227 13.483658 1.552431e-27
## Sepal.Length -0.0618848 0.04296699 -1.440287 1.518983e-01

Non, ça n’a pas fonctionné. Dans une formule, l’opérateur ^ ne signifie pas exposant. Pour demander à R d’utiliser la signification usuelle de l’opérateur, et non celle spécifique aux formules, il faut encadrer le terme contenant l’opérateur de I() comme suit :

reg <- lm(Sepal.Width ~ Sepal.Length + I(Sepal.Length^2), data = iris)

coef(summary(reg))

##                      Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)        6.41583572 1.58499197  4.047866 8.327686e-05
## Sepal.Length      -1.08556027 0.53624556 -2.024372 4.474291e-02
## I(Sepal.Length^2)  0.08570656 0.04475502  1.915016 5.743267e-02

Création de variables catégoriques pour les exemples à venir (nous verrons dans les notes sur le prétraitement de données comment utiliser la fonction cut) :

iris$Sepal.Length_catego <- cut(
  x = iris$Sepal.Length, 
  breaks = c(-Inf, quantile(iris$Sepal.Length, probs = c(1/3, 2/3)), Inf),
  right = FALSE
)
iris$Petal.Width_catego <- cut(
  x = iris$Petal.Width, 
  breaks = c(-Inf, quantile(iris$Petal.Width, probs = c(1/3, 2/3)), Inf), 
  right = FALSE
  )

5.1.1.4 Anova à 3 facteurs, modèle complet

ANOVA <- aov(Sepal.Width ~ Species*Sepal.Length_catego*Petal.Width_catego, data = iris)
# ou encore
ANOVA <- aov(
  Sepal.Width ~ (Species + Sepal.Length_catego + Petal.Width_catego)^3,
  data = iris
)

summary(ANOVA)

##                                                 Df Sum Sq Mean Sq F value   Pr(>F)    
## Species                                          2 11.345   5.672  64.620  < 2e-16 ***
## Sepal.Length_catego                              2  3.843   1.922  21.891 5.53e-09 ***
## Petal.Width_catego                               1  0.872   0.872   9.934  0.00199 ** 
## Species:Sepal.Length_catego                      3  0.077   0.026   0.291  0.83194    
## Species:Petal.Width_catego                       1  0.006   0.006   0.073  0.78754    
## Sepal.Length_catego:Petal.Width_catego           1  0.047   0.047   0.540  0.46357    
## Species:Sepal.Length_catego:Petal.Width_catego   1  0.002   0.002   0.026  0.87212    
## Residuals                                      138 12.114   0.088                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

5.1.1.5 Anova à 3 facteurs, modèle complet sans l’interaction triple

ANOVA <- aov(
  Sepal.Width ~ Species*Sepal.Length_catego*Petal.Width_catego - 
                Species:Sepal.Length_catego:Petal.Width_catego, 
  data = iris
)
# ou encore
ANOVA <- aov(
  Sepal.Width ~ (Species + Sepal.Length_catego + Petal.Width_catego)^2, 
  data = iris
)

summary(ANOVA)

##                                         Df Sum Sq Mean Sq F value   Pr(>F)    
## Species                                  2 11.345   5.672  65.076  < 2e-16 ***
## Sepal.Length_catego                      2  3.843   1.922  22.046 4.83e-09 ***
## Petal.Width_catego                       1  0.872   0.872  10.004  0.00192 ** 
## Species:Sepal.Length_catego              3  0.077   0.026   0.293  0.83046    
## Species:Petal.Width_catego               1  0.006   0.006   0.073  0.78681    
## Sepal.Length_catego:Petal.Width_catego   1  0.047   0.047   0.544  0.46199    
## Residuals                              139 12.116   0.087                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

5.1.2 Arguments accompagnant les formules

Pour les fonctions prenant une formule comme premier argument, cet argument est souvent le seul argument obligatoire.

reg <- lm(iris$Sepal.Width ~ iris$Sepal.Length)
coef(summary(reg))

##                     Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)        3.4189468 0.25356227 13.483658 1.552431e-27
## iris$Sepal.Length -0.0618848 0.04296699 -1.440287 1.518983e-01

Cependant, un argument formula est toujours accompagné d’un argument data. Typiquement, l’utilisateur fournit à data un data frame contenant en colonnes les variables à inclure dans la formule. Utiliser l’argument data permet d’alléger la formule. Les noms de variables dans la formule sont d’abord recherchés parmi les noms des éléments de data.

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris)  # (plus de iris$ dans la formule)
coef(summary(reg))

##                Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)   3.4189468 0.25356227 13.483658 1.552431e-27
## Sepal.Length -0.0618848 0.04296699 -1.440287 1.518983e-01

En plus de l’argument data, les fonctions prenant une formule en entrée ont la plupart du temps les arguments :

subset pour spécifier un sous-ensemble de données à utiliser (par défaut toutes les observations de data sont utilisées) et
na.action pour spécifier quoi faire avec les valeurs manquantes (voir help(na.fail)).

5.1.2.1 Ajustement d’un modèle sur un sous-ensemble des données

Un argument subset se spécifie comme l’argument subset de la fonction subset. Sa valeur doit être un vecteur logique dont la longueur est égale au nombre d’observations dans le jeu de données fourni à l’argument data. Voici un exemple.

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris, subset = Species == "setosa")
coef(summary(reg))

##                Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)  -0.5694327  0.5217119 -1.091470 2.805148e-01
## Sepal.Length  0.7985283  0.1039651  7.680738 6.709843e-10

5.1.2.2 Modification du traitement des valeurs manquantes

iris_2 <- iris
iris_2$Sepal.Length[6] <- NA # pour insérer une donnée manquante (pas de NA dans iris)

La valeur fournie à l’argument na.action est le nom d’une fonction qui traite les données manquantes dans un jeu de données. Le comportement par défaut de l’argument na.action est régi par l’option de session du même nom.

getOption("na.action")

## [1] "na.omit"

Dans mon cas, na.action prend donc par défaut la valeur na.omit, ce qui a pour conséquence que les observations avec au moins une valeur de variable manquante sont omises (ligne complète non considérée).

Nous pourrions fournir à l’argument une autre des fonctions listées dans la fiche d’aide help(na.fail). Par exemple, l’ajustement du modèle n’est pas effectué lorsque les données comportent des données manquantes si la valeur na.fail est fournie à na.action.

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris_2, na.action = na.fail)

## Error in na.fail.default(list(Sepal.Width = c(3.5, 3, 3.2, 3.1, 3.6, 3.9,  : 
##   missing values in object

5.2 Manipulation de la sortie

Lorsque nous affichons dans la console un objet produit en sortie d’une fonction d’ajustement de modèle, la sortie obtenue est brève.

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris)
reg

## 
## Call:
## lm(formula = Sepal.Width ~ Sepal.Length, data = iris)
## 
## Coefficients:
##  (Intercept)  Sepal.Length  
##      3.41895      -0.06188

En réalité, cet objet est une liste contenant plusieurs éléments.

str(reg, list.len = 5)

## List of 12
##  $ coefficients : Named num [1:2] 3.4189 -0.0619
##   ..- attr(*, "names")= chr [1:2] "(Intercept)" "Sepal.Length"
##  $ residuals    : Named num [1:150] 0.3967 -0.1157 0.0719 -0.0343 0.4905 ...
##   ..- attr(*, "names")= chr [1:150] "1" "2" "3" "4" ...
##  $ effects      : Named num [1:150] -37.4445 -0.6255 0.0564 -0.0485 0.471 ...
##   ..- attr(*, "names")= chr [1:150] "(Intercept)" "Sepal.Length" "" "" ...
##  $ rank         : int 2
##  $ fitted.values: Named num [1:150] 3.1 3.12 3.13 3.13 3.11 ...
##   ..- attr(*, "names")= chr [1:150] "1" "2" "3" "4" ...
##   [list output truncated]
##  - attr(*, "class")= chr "lm"

L’objet obtenu de la fonction d’ajustement de modèle ne s’affiche pas comme une liste parce qu’un attribut classe lui est attribué et que la fonction polymorphe print possède une définition spécifique aux objets de cette classe.

class(reg)

## [1] "lm"

print(reg)

## 
## Call:
## lm(formula = Sepal.Width ~ Sepal.Length, data = iris)
## 
## Coefficients:
##  (Intercept)  Sepal.Length  
##      3.41895      -0.06188

C’est une caractéristique orientée objet du langage R. Dans la terminologie de R, une fonction polymorphe est appelée fonction générique et les différentes définitions de cette fonction sont appelées méthodes. Les fonctions génériques, telles que les fonctions print, plot et summary, ont un comportement qui varie en fonction de la classe du premier argument qui leur est fourni en entrée.

Rappelons que taper le nom d’un objet dans la console est en fait un raccourci pour soumettre la fonction print avec l’objet à afficher en argument.

Si nous retirons l’attribut classe de l’objet, nous retombons sur un affichage usuel pour un objet de type liste.

class(reg) <- NULL
reg # résultat non affiché, car trop long

L’attribut classe peut même contenir plus d’une classe.

ANOVA <- aov(Sepal.Width ~ Species, data = iris)
class(ANOVA)

## [1] "aov" "lm"

Souvent, le nom de la classe d’un objet est le nom de la fonction qui a produit cet objet. Les objets retournés par la fonction aov ont deux classes, car en réalité la fonction aov appelle la fonction lm.

5.2.1 Fonctions génériques d’extraction d’information

Voici la liste des fonctions génériques les plus couramment utilisées pour tirer de l’information d’un objet produit par une fonction d’ajustement de modèle :

summary : pour afficher un résumé des informations plus long que ce qui est affiché avec print et pour produire des résultats supplémentaires;
coef (ou son alias coefficients) et confint : pour afficher les coefficients et pour produire des intervalles de confiance pour les coefficients d’un modèle;
residuals et fitted : pour extraire les résidus et les valeurs prédites;
predict : pour effectuer des prédictions pour de nouvelles observations;
anova : pour calculer la table d’analyse de la variance (ANOVA) du modèle;
model.tables et TukeyHSD (pour la classe aov) : pour calculer les moyennes par niveaux de facteurs et pour faire des comparaisons multiples de Tukey sur ces moyennes;
deviance, logLik, AIC, BIC : pour extraire la déviance, la log-vraisemblance maximisée, le AIC et le BIC.

L’utilisation de ces fonctions est la façon usuelle en R d’extraire des résultats relatifs à un modèle. Par exemple, pour extraire les coefficients d’un modèle, nous pouvons utiliser :

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris)
coef(reg)

##  (Intercept) Sepal.Length 
##    3.4189468   -0.0618848

Notons cependant qu’il est aussi possible d’extraire cette information en accédant directement aux éléments de reg, qui est une liste.

reg$coefficients

##  (Intercept) Sepal.Length 
##    3.4189468   -0.0618848

Voici quelques exemples d’utilisation des fonctions d’extraction d’information :

reg <- lm(Sepal.Width ~ Sepal.Length + Petal.Width, data = iris)
summary(reg)

## 
## Call:
## lm(formula = Sepal.Width ~ Sepal.Length + Petal.Width, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.99563 -0.24690 -0.00503  0.23354  1.01131 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.92632    0.32094   6.002 1.45e-08 ***
## Sepal.Length  0.28929    0.06605   4.380 2.24e-05 ***
## Petal.Width  -0.46641    0.07175  -6.501 1.17e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3841 on 147 degrees of freedom
## Multiple R-squared:  0.234,  Adjusted R-squared:  0.2236 
## F-statistic: 22.46 on 2 and 147 DF,  p-value: 3.091e-09

confint(reg)

##                   2.5 %     97.5 %
## (Intercept)   1.2920761  2.5605655
## Sepal.Length  0.1587655  0.4198079
## Petal.Width  -0.6082076 -0.3246210

str(residuals(reg))

##  Named num [1:150] 0.1916 -0.25054 0.00731 -0.06376 0.32053 ...
##  - attr(*, "names")= chr [1:150] "1" "2" "3" "4" ...

predict(
  reg, 
  newdata = data.frame(
    Sepal.Length = c(5, 6),
    Petal.Width = c(1, 2)
  )
)

##        1        2 
## 2.906340 2.729213

ANOVA <- aov(Sepal.Width ~ Species + Sepal.Length_catego, data = iris)
summary(ANOVA)

##                      Df Sum Sq Mean Sq F value   Pr(>F)    
## Species               2 11.345   5.672   62.70  < 2e-16 ***
## Sepal.Length_catego   2  3.843   1.922   21.24 8.13e-09 ***
## Residuals           145 13.119   0.090                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

anova(ANOVA)

## Analysis of Variance Table
## 
## Response: Sepal.Width
##                      Df  Sum Sq Mean Sq F value    Pr(>F)    
## Species               2 11.3449  5.6725  62.697 < 2.2e-16 ***
## Sepal.Length_catego   2  3.8433  1.9216  21.240 8.129e-09 ***
## Residuals           145 13.1187  0.0905                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

model.tables(ANOVA, type = "means")

## Tables of means
## Grand mean
##          
## 3.057333 
## 
##  Species 
##     setosa versicolor virginica
##      3.428       2.77     2.974
## rep 50.000      50.00    50.000
## 
##  Sepal.Length_catego 
##     [-Inf,5.4) [5.4,6.3) [6.3, Inf)
##          2.919     3.081      3.157
## rep     46.000    53.000     51.000

TukeyHSD(ANOVA)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Sepal.Width ~ Species + Sepal.Length_catego, data = iris)
## 
## $Species
##                        diff         lwr        upr     p adj
## versicolor-setosa    -0.658 -0.80045516 -0.5155448 0.0000000
## virginica-setosa     -0.454 -0.59645516 -0.3115448 0.0000000
## virginica-versicolor  0.204  0.06154484  0.3464552 0.0025694
## 
## $Sepal.Length_catego
##                             diff         lwr       upr     p adj
## [5.4,6.3)-[-Inf,5.4)  0.16172436  0.01819230 0.3052564 0.0229762
## [6.3, Inf)-[-Inf,5.4) 0.23756010  0.09272626 0.3823939 0.0004549
## [6.3, Inf)-[5.4,6.3)  0.07583574 -0.06387887 0.2155503 0.4057167

5.2.2 Résultats additionnels fournis par `summary`

La fonction générique summary ne fait pas que produire un affichage du modèle ajusté plus complet que la fonction générique print. Elle produit des résultats supplémentaires concernant le modèle. Par exemple, pour un modèle produit avec lm, comparons ce que produit directement la fonction lm et ce que produit la fonction générique summary pour un objet retourné par lm.

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris)
reg_summary <- summary(reg)
sort(names(reg))

##  [1] "assign"        "call"          "coefficients"  "df.residual"   "effects"      
##  [6] "fitted.values" "model"         "qr"            "rank"          "residuals"    
## [11] "terms"         "xlevels"

sort(names(reg_summary))

##  [1] "adj.r.squared" "aliased"       "call"          "coefficients"  "cov.unscaled" 
##  [6] "df"            "fstatistic"    "r.squared"     "residuals"     "sigma"        
## [11] "terms"

Seulement 4 éléments de la liste reg portent des noms aussi présents dans la liste reg_summary. Et des éléments de même nom dans les deux listes ne contiennent pas toujours la même chose.

reg$coefficients

##  (Intercept) Sepal.Length 
##    3.4189468   -0.0618848

reg_summary$coefficients

##                Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)   3.4189468 0.25356227 13.483658 1.552431e-27
## Sepal.Length -0.0618848 0.04296699 -1.440287 1.518983e-01

Les éléments produits par summary tendent à contenir plus de détails que les éléments obtenus directement de lm.

La fonction summary réalise donc des calculs supplémentaires relatifs au modèle. Par exemple, pour un modèle ajusté avec lm, elle réalise les tests sur les termes du modèle et calcule le coefficient de détermination (R²), soit une mesure souvent utilisée pour évaluer la qualité de la prédiction du modèle.

reg_summary$r.squared

## [1] 0.01382265

Pour un modèle d’analyse de la variance ajusté avec aov, la fonction summary produit la table d’ANOVA complète, tout comme la fonction anova le fait.

ANOVA <- aov(Sepal.Width ~ Species + Sepal.Length_catego, data = iris)
ANOVA_summary <- summary(ANOVA)
str(ANOVA_summary)

## List of 1
##  $ :Classes 'anova' and 'data.frame':    3 obs. of  5 variables:
##   ..$ Df     : num [1:3] 2 2 145
##   ..$ Sum Sq : num [1:3] 11.34 3.84 13.12
##   ..$ Mean Sq: num [1:3] 5.6725 1.9216 0.0905
##   ..$ F value: num [1:3] 62.7 21.2 NA
##   ..$ Pr(>F) : num [1:3] 2.40e-20 8.13e-09 NA
##  - attr(*, "class")= chr [1:2] "summary.aov" "listof"

5.2.3 Mise en forme avec le package `broom`

Le package broom offre des fonctions pour faciliter la manipulation de sorties d’une fonction d’ajustement de modèle. Les trois principales fonctions de ce package sont les suivantes :

tidy : produit un résumé des principaux résultats statistiques d’un modèle, dans le cas d’un modèle linéaire il s’agit d’une table des tests sur les coefficients du modèle;
augment : ajoute aux données sur lesquelles le modèle a été ajusté des informations tirées du modèle, comme des résidus et des valeurs prédites;
glance : réunit dans un seul data frame à une ligne plusieurs statistiques globales au modèle, comme des statistiques d’ajustement du modèle.

Voici quelques exemples :

reg <- lm(Sepal.Width ~ Sepal.Length, data = iris)

library(broom)
tidy(reg) # très similaire à coef(summary(reg)) pour une sortie de lm

## # A tibble: 2 x 5
##   term         estimate std.error statistic  p.value
##   <chr>           <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    3.42      0.254      13.5  1.55e-27
## 2 Sepal.Length  -0.0619    0.0430     -1.44 1.52e- 1

head(augment(reg))

## # A tibble: 6 x 8
##   Sepal.Width Sepal.Length .fitted  .resid    .hat .sigma   .cooksd .std.resid
##         <dbl>        <dbl>   <dbl>   <dbl>   <dbl>  <dbl>     <dbl>      <dbl>
## 1         3.5          5.1    3.10  0.397  0.0121   0.435 0.00516       0.919 
## 2         3            4.9    3.12 -0.116  0.0154   0.436 0.000563     -0.269 
## 3         3.2          4.7    3.13  0.0719 0.0195   0.436 0.000277      0.167 
## 4         3.1          4.6    3.13 -0.0343 0.0218   0.436 0.0000709    -0.0798
## 5         3.6          5      3.11  0.490  0.0136   0.434 0.00893       1.14  
## 6         3.9          5.4    3.08  0.815  0.00859  0.431 0.0154        1.89

glance(reg)

## # A tibble: 1 x 12
##   r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC deviance df.residual
##       <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <int>
## 1    0.0138       0.00716 0.434      2.07   0.152     1  -86.7  179.  188.     27.9         148
## # ... with 1 more variable: nobs <int>

Plus d’informations peuvent être trouvées dans la documentation du package : https://broom.tidymodels.org/

6 Résumé

Statistiques descriptives

Calcul	opère de façon vectorielle	combine, retourne une valeur	combine, retourne valeur(s)	combine, retourne un vecteur
mesure de position	`pmin`, `pmax`	`min`, `max`, `which.min`, `which.max`	`range`, `quantile`, `summary`	`cummin`, `cummax`, `rank`
tendance centrale		`mean`, `median`	`summary`
dispersion		`sd`, `IQR`, `mad`	`var`, `cov`, `cor`
fréquences			`table`, `ftable`, `xtabs`, `summary`

Traitement des données manquantes :
- argument na.rm ,
- fonction na.omit;
calcul de fréquences marginales ou relatives à partir d’un tableau de fréquences :
marginSums, addmargins, proportions.
énumération de combinaisons : expand.grid, combn.

Distributions de probabilité et génération de nombres aléatoires

Famille de fonction	Description
`d*`	fonction de densité de la distribution `*`
`p*`	fonction de répartition de la distribution `*`
`q*`	fonction quantile de la distribution `*`
`r*`	génération pseudo-aléatoirement d’observations selon la distribution `*`

Liste de toutes les distributions * offertes en R de base : help(Distributions)

fonction sample (ou sample.int) : tirage aléatoire d’échantillons
fonction set.seed : pour fixer le germe du tirage pseudo-aléatoire

Tests statistiques

Quelques fonctions R pour faire des tests statistiques de base :

tests sur une ou des moyennes : t.test;
tests sur une ou des proportions : prop.test, binom.test;
tests de comparaison de variances : var.test, bartlett.test;
tests sur une corrélation : cor.test;
tests pour une distribution : shapiro.test, ks.test;
tests non paramétriques : wilcox.test, kruskal.test, friedman.test;
tests sur des fréquences : méthode summary pour un objet de classe table (produit par la fonction table ou xtabs), chisq.test, fisher.test, mantelhaen.test.

Ajustement de modèles

Quelques fonctions R pour ajuster des modèles :

modèles linéaires, dont la régression : lm;
modèle d’analyse de la variance : lm ou aov;
modèles linéaires généralisés : glm;
modèles linéaires mixtes (peuvent contenir des effets aléatoires) : lmer du package lme4 ou lme du package nlme;
modèles non linéaires : nls.

Formules R

Écriture générale : y ~ x1 + x2
où y = variable réponse, x1 et x2 = variables explicatives.

Opérateurs acceptés et leur signification :

+ pour ajouter des termes;
- pour soustraire des termes;
- 1 ou + 0 pour retirer l’ordonnée à l’origine;
. pour représenter toutes les variables dans le jeu de données, autres que la variable mise à la gauche du ~ ;
: pour les termes d’interaction entre facteurs;
* pour le croisement de facteurs;
^ croisement de facteurs jusqu’à un certain niveau d’interaction;
%in% pour les facteurs emboîtés;
| pour un conditionnement ou spécifier des effets aléatoires

I() pour utiliser la signification usuelle des opérateurs et non celle spécifique aux formules.

Sortie d’une fonction d’ajustement de modèle

Affichage (print) vs liste contenant les objets retournés

La liste retournée a une ou des classes $\rightarrow$ programmation orientée objet

Fonctions pour tirer de l’information d’un objet produit par une fonction d’ajustement de modèle :

summary : plus de résultats relatifs au modèle + affichage d’un résumé des informations;
coef (ou son alias coefficients) et confint : coefficients et leurs intervalles de confiance;
residuals et fitted : résidus et valeurs prédites;
predict : prédiction pour une nouvelle observation;
anova : table d’analyse de la variance du modèle;
model.tables et TukeyHSD (pour la classe aov) : moyennes par niveaux de facteurs et comparaisons multiples de Tukey;
deviance, logLik, AIC, BIC : déviance, log-vraisemblance maximisée, AIC et BIC.

Références

Les informations présentées dans ces notes proviennent des fiches d’aide du logiciel R :

R Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/

Le manuel suivant de R contient aussi plusieurs informations concernant les calculs statistiques en R :

R Core Team (2020). An Introduction to R. R version 4.0.3. URL https://cran.r-project.org/doc/manuals/r-release/R-intro.html

Documentation du package mentionné qui ne vient pas avec l’installation de base de R :

package broom :
- page web du package sur le CRAN : https://CRAN.R-project.org/package=broom
- documentation du package : https://broom.tidymodels.org/

Une très grande quantité de méthodes statistiques sont implémentées en R. Voici quelques bonnes références sur le sujet.

Livres :
- Hothorn, T. et Everitt, B.S. (2014). A Handbook of Statistical Analyses Using R, third edition. CRC Press.
- Millot, G. (2018). Comprendre et réaliser les tests statistiques à l’aide de R: manuel de biostatistique, 4^e édition. De Boeck Supérieur.
Sites web contenant plusieurs exemples d’analyses statistiques en R :
- https://stats.idre.ucla.edu/other/dae/ (contient aussi les mêmes exemples avec d’autres logiciels statistiques)
- https://www.statmethods.net/about/sitemap.html
Ressources pour dénicher des packages R implémentant des méthodes statistiques particulières :
- Task views de R : http://cran.r-project.org/web/views/
- Dépôt informatique de packages R en bio-informatique : http://www.bioconductor.org/

Pour aller plus loin :

Braun, W. J. et Murdoch, D. (2007). A First Course in Statistical Programming with R. Cambridge University Press.

Calculs statistiques en R

Sophie Baillargeon, Université Laval

2021-02-24

1 Statistiques descriptives

1.1 Fonctions retournant une seule statistique

Fonctions which.max et which.min

1.1.1 Traitement des données manquantes et argument na.rm

1.2 Fonctions pouvant retourner plusieurs statistiques

Fonctions range et quantile

Fonction summary

Fonctions var, cov et cor

1.3 Fonctions retournant un vecteur de statistiques

Fonctions cummin et cummax

Fonctions pmin et pmax

Fonction rank

1.4 Calcul de fréquences

Fonctions table

Fonctions ftable

Fonctions xtabs

Autres fonctions relatives au calcul de fréquences

Transformation du format d’un objet de classe "table"

1.5 Énumération de combinaisons

2 Distributions de probabilité

2.1 Fonction de densité

Exemple : distribution binomiale

Exemple : distribution normale standard

2.2 Fonction de répartition

Exemple : distribution normale standard

2.3 Fonction quantile

Exemple : distribution normale standard

3 Génération de nombres pseudo-aléatoires

3.1 Fonction sample

3.2 Germe de la génération pseudo-aléatoire

4 Tests statistiques

Exemple : test t bilatéral de comparaison de moyennes, avec variances inégales

Exemple : test non paramétrique équivalent

5 Ajustement de modèles

Exemple : régression linéaire simple entre la largeur et la longueur des sépales

Exemple : ANOVA pour comparer les largeurs de sépales moyennes entre toutes les espèces

5.1 Formules

5.1.1 Exemples

5.1.1.1 Retrait de l’ordonnée à l’origine

5.1.1.2 Régression log-log

5.1.1.3 Régression polynomiale

5.1.1.4 Anova à 3 facteurs, modèle complet

5.1.1.5 Anova à 3 facteurs, modèle complet sans l’interaction triple

5.1.2 Arguments accompagnant les formules

5.1.2.1 Ajustement d’un modèle sur un sous-ensemble des données

5.1.2.2 Modification du traitement des valeurs manquantes

5.2 Manipulation de la sortie

5.2.1 Fonctions génériques d’extraction d’information

5.2.2 Résultats additionnels fournis par summary

5.2.3 Mise en forme avec le package broom

6 Résumé

Statistiques descriptives

Distributions de probabilité et génération de nombres aléatoires

Tests statistiques

Ajustement de modèles

Formules R

Sortie d’une fonction d’ajustement de modèle

Références

Fonctions `which.max` et `which.min`

1.1.1 Traitement des données manquantes et argument `na.rm`

Fonctions `range` et `quantile`

Fonction `summary`

Fonctions `var`, `cov` et `cor`

Fonctions `cummin` et `cummax`

Fonctions `pmin` et `pmax`

Fonction `rank`

Fonctions `table`

Fonctions `ftable`

Fonctions `xtabs`

Transformation du format d’un objet de classe `"table"`

3.1 Fonction `sample`

5.2.2 Résultats additionnels fournis par `summary`

5.2.3 Mise en forme avec le package `broom`