Graphiques en R
Sophie Baillargeon, Université Laval
2021-02-25
- 1 Introduction
- 2 Système graphique de base
- 2.1 Procédure de création d’un graphique
- 2.2 Fonction générique
plot - 2.3 Différentes fonctions graphiques
- 2.3.1 Diagramme de dispersion - fonctions
plot.default,pairsetmatplot - 2.3.2 Diagramme en lignes - fonctions
plot.defaultetmatplot - 2.3.3 Diagramme en secteurs - fonction
pie - 2.3.4 Diagramme à barres - fonction
barplot - 2.3.5 Diagramme en points de Cleveland - fonction
dotchart - 2.3.6 Diagramme en mosaïque - fonction
mosaicplot - 2.3.7 Histogramme - fonction
hist - 2.3.8 Diagramme en boîte - fonction
boxplot - 2.3.9 Courbe d’estimation de densité à noyau - méthode
plot.density - 2.3.10 Diagramme quantile-quantile - fonctions
qqnormetqqplot - 2.3.11 Représentation graphique d’une expression mathématique - fonction
curve
- 2.3.1 Diagramme de dispersion - fonctions
- 2.4 Modification de l’ordre des niveaux d’un facteur
- 2.5 Arguments et paramètres graphiques
- 2.6 Ajout d’éléments à un graphique
- 2.7 Possibilités graphiques spécifiques
- 2.8 Aspects techniques
- 2.9 Point de vue
- 3 Package
lattice - 4 Package
ggplot2 - 5 Autres possibilités graphiques en R
- 6 Conclusion
- 7 Résumé
- Références
- Annexe
Note préliminaire : Lors de leur dernière mise à jour, ces notes ont été révisées en utilisant R 4.0.3, le package lattice version 0.20-41 et le package maps version 3.3.0. Pour d’autres versions, les informations peuvent différer.
1 Introduction
La visualisation graphique, une étape importante en analyse de données
La communauté statistique insiste depuis longtemps sur l’importance de visualiser graphiquement des données avant de les analyser. En 1973, Anscombe [1] publiait les quatre jeux de données suivants, ayant les mêmes paramètres estimés de régression linéaire simple (y=3+0.5x), mais présentant des relations bien différentes!
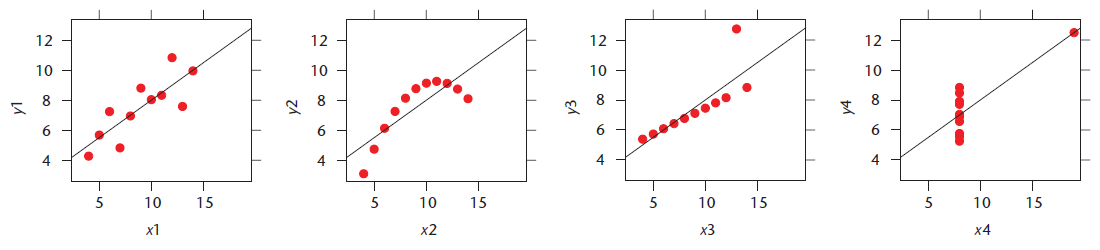
Plusieurs autres exemples de jeux de données possédant les mêmes statistiques descriptives, mais des représentations graphiques très différentes ont été publiés depuis (voir [2]).
Certains ont même mis en évidence l’importance de représenter graphiquement des données de plusieurs manières différentes afin de découvrir les surprises qu’elles peuvent cacher. Par exemple, les données suivantes, créées pour enseigner à des étudiants l’importance des graphiques en analyse de données [3], forment le mot SUPERMAN si elles sont représentées sur une échelle adéquatement transformée et si les observations des deux groupes sont superposées.
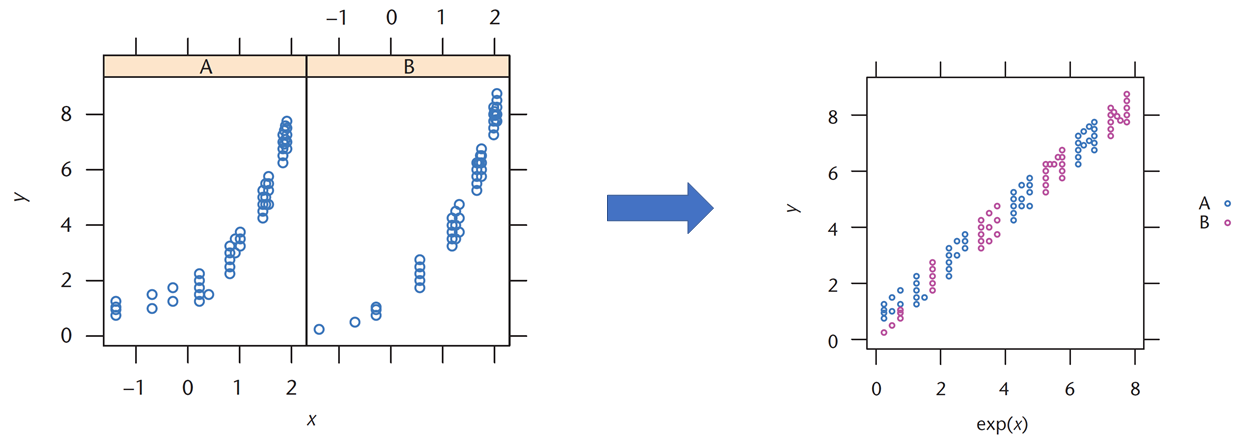
Les graphiques, une force de R
En plus d’être un environnement de calculs statistiques, R permet de produire des graphiques. Il s’agit d’une utilité importante de R. La toute première phrase du site web de R mentionne cette utilité.
« R is a free software environment for statistical computing and graphics. »
Lors de comparaison entre R et d’autres logiciels permettant de faire de l’analyse de données, les capacités graphiques de R sont souvent considérées comme un de ses meilleurs atouts. L’installation de base de R comporte beaucoup de fonctions graphiques, dont plusieurs sont présentées ici. Elles permettent de produire des graphiques pour lesquels l’utilisateur garde le plein contrôle sur l’apparence du graphique.
De plus, deux packages offrent des fonctions pouvant remplacer plusieurs des fonctions graphiques de base de R. Chacun de ces packages est tellement complet qu’il peut être qualifié de système graphique. Il s’agit des packages suivants :
lattice: package graphique qui met l’emphase sur les représentations multivariées,ggplot2: package graphique conçu en ayant comme objectif la simplicité d’utilisation et la qualité des graphiques produits.
Le package lattice n’est présenté que très brièvement dans ce document, étant donné qu’il est de moins en moins utilisé. Le package ggplot2 vit cependant le phénomène inverse : il est très populaire et est même devenu un incontournable pour la création de graphiques en R. Une fiche à part des notes lui est donc consacrée.
Pour finir, quelques autres possibilités graphiques en R sont mentionnées rapidement à la fin de ce document, notamment les :
- graphiques 3D,
- graphiques interactifs,
- cartes géographiques.
La grande quantité de possibilités graphiques en R contribue à en faire un puissant outil de visualisation de données.
Présentation des données utilisées pour les exemples
Plusieurs des exemples de graphiques de ces notes représentent les mêmes données : celles stockées dans le data frame quakes du package datasets (chargé par défaut lors de l’ouverture de session).
str(quakes)## 'data.frame': 1000 obs. of 5 variables:
## $ lat : num -20.4 -20.6 -26 -18 -20.4 ...
## $ long : num 182 181 184 182 182 ...
## $ depth : int 562 650 42 626 649 195 82 194 211 622 ...
## $ mag : num 4.8 4.2 5.4 4.1 4 4 4.8 4.4 4.7 4.3 ...
## $ stations: int 41 15 43 19 11 12 43 15 35 19 ...Il s’agit d’observations pour 1000 évènements sismiques survenus près des îles Fidji depuis 1964. Pour chaque évènement, nous avons :
latetlong: sa localisation géographique en latitude-longitude,depth: sa profondeur,mag: sa magnitude etstations: le nombre de stations sismiques ayant rapporté l’évènement.
Pour certains exemples, nous aurons besoin de variables catégoriques stockées sous forme de facteur. Ajoutons donc les deux variables supplémentaires suivantes au jeu de données quakes :
mag_catego: magnitude du séisme arrondie à l’entier inférieur (4, 5 ou 6),region: région où à eu lieu le séisme ("Ouest"ou"Est").
quakes$mag_catego <- factor(floor(quakes$mag))
quakes$region <- factor(
ifelse(quakes$long < 175, yes = "Ouest", no = "Est"),
levels = c("Ouest", "Est")
)
str(quakes)## 'data.frame': 1000 obs. of 7 variables:
## $ lat : num -20.4 -20.6 -26 -18 -20.4 ...
## $ long : num 182 181 184 182 182 ...
## $ depth : int 562 650 42 626 649 195 82 194 211 622 ...
## $ mag : num 4.8 4.2 5.4 4.1 4 4 4.8 4.4 4.7 4.3 ...
## $ stations : int 41 15 43 19 11 12 43 15 35 19 ...
## $ mag_catego: Factor w/ 3 levels "4","5","6": 1 1 2 1 1 1 1 1 1 1 ...
## $ region : Factor w/ 2 levels "Ouest","Est": 2 2 2 2 2 2 1 2 2 2 ...2 Système graphique de base
Les graphiques de base en R sont créés grâce aux fonctions provenant des packages graphics et grDevices développés par le R core team. Ces packages sont intégrés à l’installation de base de R et ils sont chargés par défaut lors de l’ouverture d’une session R. Dans cette section, nous couvrirons les possibilités de ces packages.
2.1 Procédure de création d’un graphique
Un programme pour créer un graphique avec le système graphique de base en R se décompose typiquement en 3 étapes, les suivantes :
- La configuration des paramètres graphiques (au besoin) :
- L’initialisation d’un graphique :
- L’ajout séquentiel d’éléments au graphique (au besoin) :
Lorsque les paramètres graphiques sont modifiés avec un appel à la fonction par au début du programme, une bonne pratique est d’ajouter aussi à la fin du programme une commande pour redonner aux paramètres graphiques leurs valeurs par défaut.
La mise en forme et les annotations du graphique (p. ex. titre et noms d’axe) sont déterminées par les paramètres graphiques ainsi que par des arguments des fonctions graphiques. Avec un peu de patience et quelques lignes de code, il est possible d’arriver à contrôler parfaitement l’apparence du graphique.
Voici un exemple de programme créant un graphique avec le système graphique de base en R.
# 1. Configuration de paramètres graphiques
par_default <- par(bty = 'n')
# 2. Initialisation d'un graphique (contenant ici des diagrammes en boîtes)
plot(
stations ~ mag_catego, data = quakes,
lwd = 1.5, outline = FALSE,
main = "Nombres de stations ayant rapporté les séismes\nselon leurs classes de magnitude",
xlab = "classe de magnitude",
ylab = "nombre de stations"
)
# 3. Ajout séquentiel d'éléments au graphique
# Ajout de diagrammes de dispersion 1D par région
stripchart(
stations ~ mag_catego, data = quakes, subset = region == "Ouest",
method = "jitter", jitter = 0.3, add = TRUE, vertical = TRUE,
col = rgb(1,0,0,0.2), pch = 20
)
stripchart(
stations ~ mag_catego, data = quakes, subset = region == "Est",
method = "jitter", jitter = 0.3, add = TRUE, vertical = TRUE,
col = rgb(0,0,1,0.2), pch = 20
)
# Ajout d'une légende
legend(
x = "bottomright", bty = "n",
col = c(rgb(1,0,0,0.5), rgb(0,0,1,0.5)), pch = 20,
legend = c("Ouest", "Est"), title = "région"
)
# Réattribution des valeurs par défaut aux paramètres graphiques modifiés
par(par_default)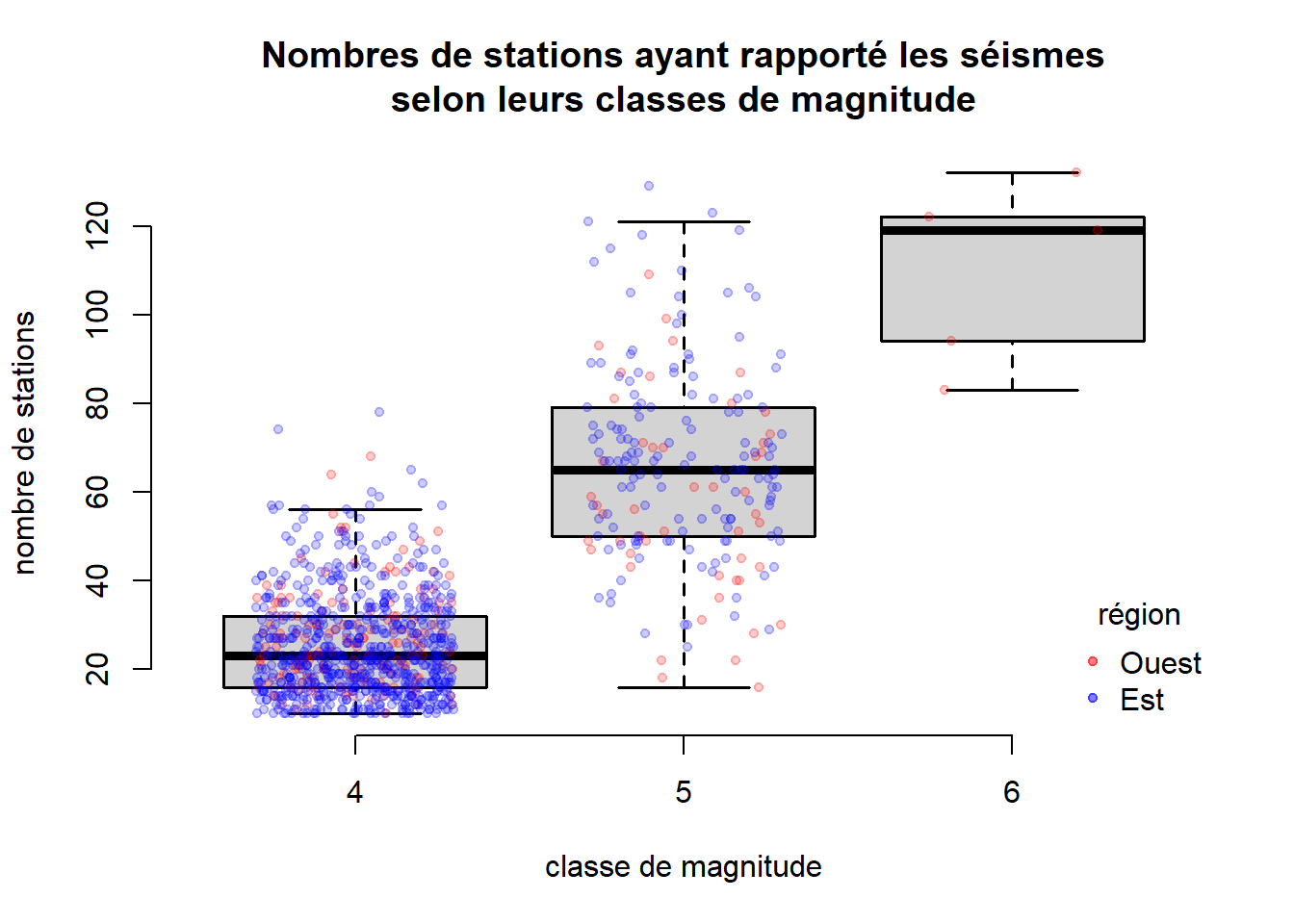
Les prochaines sections présentent les concepts à connaître pour suivre la procédure de création de graphique avec le système graphique de base en R et contiennent beaucoup d’exemples. Cependant, la matière n’est pas couverte dans le même ordre que les étapes de la procédure. Même si dans le code de création d’un graphique la configuration des paramètres est l’étape 1, il faut d’abord savoir créer un graphique pour que cette étape ait du sens. De plus, la configuration des paramètres graphique est une étape facultative. Parfois, les valeurs par défaut des paramètres font l’affaire.
Ainsi, nous allons d’abord étudier la principale fonction du système graphique de base en R, soit la fonction plot. Dans un deuxième temps, nous ferons un survol de plusieurs autres fonctions de création de graphiques. Ensuite, les arguments et paramètres graphiques qui permettent de contrôler les annotations et la mise en forme seront présentés. Pour terminer la couverture des étapes de la procédure de création, il ne restera plus qu’à parler des fonctions d’ajouts d’éléments à un graphique.
Les exemples présentés seront simple au début, mais se complexifient au fil de la section.
2.2 Fonction générique plot
La principale fonction graphique en R est la fonction plot. En fait, plot est une fonction générique. Il existe plusieurs méthodes associées à cette fonction générique. Pour afficher la liste des méthodes plot chargées dans notre session R, il faut soumettre la commande suivante.
methods(plot)## [1] plot.acf* plot.data.frame* plot.decomposed.ts* plot.default
## [5] plot.dendrogram* plot.density* plot.ecdf plot.factor*
## [9] plot.formula* plot.function plot.hclust* plot.histogram*
## [13] plot.HoltWinters* plot.isoreg* plot.lm* plot.medpolish*
## [17] plot.mlm* plot.ppr* plot.prcomp* plot.princomp*
## [21] plot.profile.nls* plot.raster* plot.spec* plot.stepfun
## [25] plot.stl* plot.table* plot.ts plot.tskernel*
## [29] plot.TukeyHSD*
## see '?methods' for accessing help and source codeSi nous donnons en entrée à la fonction plot un vecteur en argument x, c’est la méthode plot.default qui est utilisée. Cette méthode trace un diagramme de dispersion.
La fonction plot choisit la méthode à utiliser en fonction de la classe de l’objet assigné à son premier argument (x). C’est une caractéristique « orientée objet » du langage R. Nous reviendrons sur ce concept plus tard. Pour l’instant, il suffit de comprendre que les différentes méthodes produisent différents résultats et acceptent différents arguments. En fait, ces méthodes font souvent appels à d’autres fonctions de création de graphique.
L’annexe contient une panoplie d’exemples de graphiques pouvant être produits avec la fonction générique plot, selon les objets qui lui sont donnés en entrée. Voici ici un résumé des possibilités couvertes dans ces exemples.
Résumé de graphiques usuels produits par plot
Type x |
Type y |
Graphique produit (méthode utilisée → fonction ou autre méthode appelée) |
|---|---|---|
| vecteur | - | diagramme de dispersion en fonction de l’index des observations (plot.default) |
| vecteur | diagramme de dispersion (plot.default) |
|
| facteur | - | diagramme à barres (plot.factor → barplot) |
| vecteur | diagrammes en boîtes juxtaposées (plot.factor → boxplot) |
|
| facteur | diagramme en mosaïque (plot.factor → spineplot) |
|
| data frame | - | dépend du nombre de variables, de leur ordre et de leurs natures (plot.data.frame → pairs, plot.default, plot.factor ou stripchart) |
| formule | - | dépend de la position des variables dans la formule et de leurs natures (plot.formula → plot.default, plot.factor ou plot.data.frame) |
| fonction | - | courbe (plot.function → curve) |
La fonction plot peut en faire beaucoup plus que ça grâce à ses nombreuses méthodes. Par exemple, comme nous l’avons déjà mentionné dans les notes sur les concepts de base en R, si elle reçoit en entrée la sortie d’un appel à la fonction lm, qui ajuste un modèle linéaire à des données, elle produit des graphiques de résidus de ce modèle via sa méthode plot.lm.
2.3 Différentes fonctions graphiques
En explorant les capacités de la fonction générique plot, nous découvrons plusieurs fonctions de création de graphiques. Ces fonctions permettent de créer des graphiques de différents types.
Voici un résumé des principaux types de graphiques pouvant être créés dans le système graphique de base en R, suivi d’exemples.
Représentations d’une variable (observations stockées dans x) :
| Type de graphique | Exemple d’appel de fonction | Type de x |
|---|---|---|
| diagramme en secteurs (pie chart) | pie(table(x), ...) |
facteur |
| diagramme à barres (bar plot) | barplot(table(x), ...) |
facteur |
| diagramme en points de Cleveland | dotchart(table(x), ...) |
facteur |
| histogramme | hist(x, ...) |
vecteur numérique |
| courbe de densité à noyau (kernel density plot) | plot(density(x), ...) → méthode plot.density |
vecteur numérique |
| diagramme en boîte (boxplot) | boxplot(x, ...) |
vecteur numérique |
| diagramme quantile-quantile théorique normal | qqnorm(x, ...) |
vecteur numérique |
Représentation d’une expression mathématique : curve(expr, ...)
Représentations de deux variables (observations stockées dans x et y) :
| Type de graphique | Exemple d’appel de fonction | Type de x |
Type de y |
|---|---|---|---|
| diagramme à barres empilées ou groupées | barplot(table(x, y), ...) avec beside = TRUE pour barres groupées |
facteur | facteur |
| diagramme en points de Cleveland | dotchart(table(x, y), ...) |
facteur | facteur |
| diagramme en mosaïque | mosaicplot(table(x, y), ...) |
facteur | facteur |
| diagrammes en boîte juxtaposés | boxplot(y ~ x, ...) |
facteur | vecteur numérique |
| diagramme de dispersion (scatterplot) ou en lignes (line chart) | plot(x, y, ...) → méthode plot.default |
vecteur numérique | vecteur numérique |
| diagramme quantile-quantile empirique | qqplot(x, y, ...) |
vecteur numérique | vecteur numérique |
Représentation de plus de trois variables numériques :
- matrice de diagrammes de dispersion :
pairs( ~ x + y + z, ...) - diagrammes de dispersion superposés :
matplot(matriceX, matriceY, ...)
2.3.1 Diagramme de dispersion - fonctions plot.default, pairs et matplot
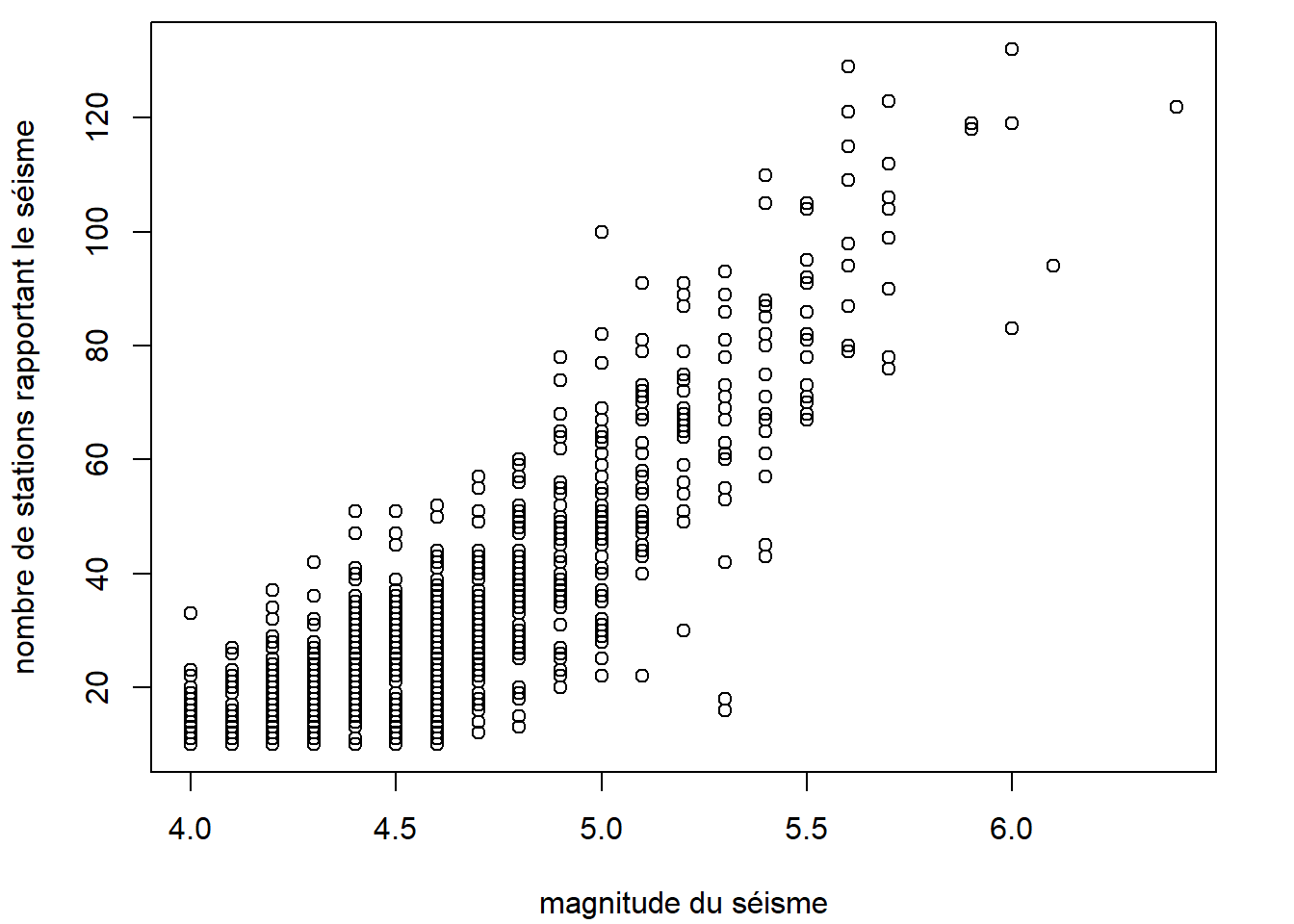
La méthode plot.default (via la fonction générique plot ou directement) produit par défaut un diagramme de dispersion (en anglais scatterplot), aussi appelé nuage de points.
plot(
x = quakes$mag, y = quakes$stations,
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
La fonction pairs produit quant à elle une matrice de diagrammes de dispersion entre plusieurs paires de variables.
pairs( ~ depth + mag + stations, data = quakes)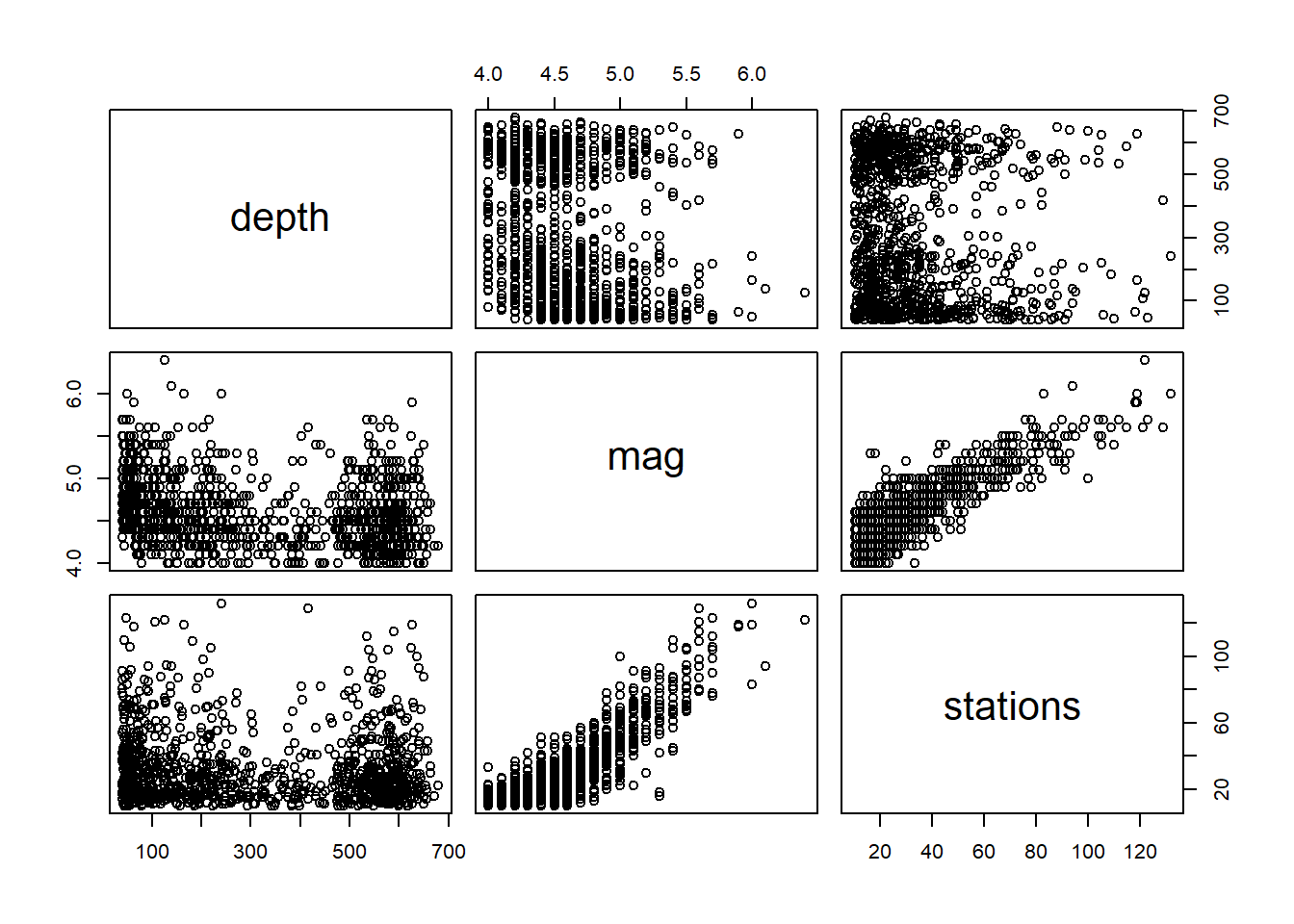
La fonction matplot permet de facilement superposer plusieurs diagrammes de dispersion. Elle associe les colonnes de la structure à deux dimensions fournie en x à celles de la structure à deux dimensions fournie en y (colonne i de x associée à la colonne i de y). Voici un exemple d’utilisation de cette fonction exploitant un jeu de données créé à partir de quakes contenant les valeurs des variables mag et stations dans des colonnes distinctes par région.
quakes_large <- reshape(
data = quakes,
direction = "wide",
idvar = c("lat", "long", "depth"),
timevar = "region",
v.names = c("mag", "stations"),
sep = "_"
)
matplot(
x = quakes_large[, c("mag_Est", "mag_Ouest")],
y = quakes_large[, c("stations_Est", "stations_Ouest")],
pch = 2:1, col = c("blue", "green"),
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)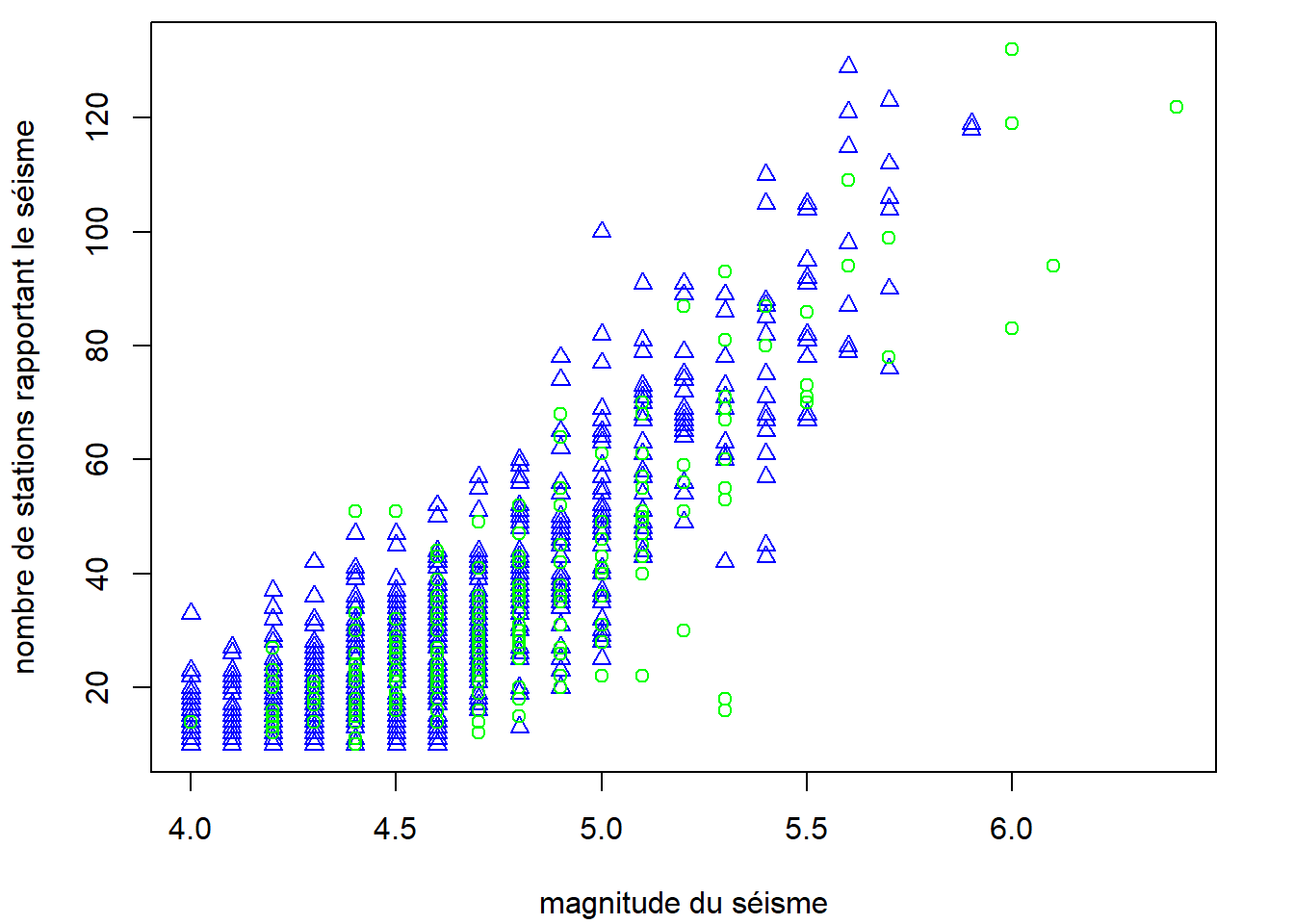
Il faudrait ajouter une légende au graphique pour indiquer la signification des deux symboles et couleurs de points. La fonction matplot ne peut pas faire cet ajout. Il devra donc être fait avec la fonction legend, que nous verrons plus loin.
2.3.2 Diagramme en lignes - fonctions plot.default et matplot
En assignant la valeur "l" à l’argument type de la méthode plot.default, celle-ci produit un diagramme en lignes (en anglais line chart), aussi appelé diagramme à lignes brisées. Ce type de graphique est couramment employé pour représenter l’évolution temporelle d’une variable.
Voici un exemple de diagramme en lignes exploitant un jeu de données créé à partir de quakes contenant les valeurs moyennes de nombres de stations par valeur de magnitude.
mean_stations_per_mag <- aggregate(stations ~ mag, data = quakes, FUN = mean)
plot(
stations ~ mag,
data = mean_stations_per_mag,
type = "l",
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)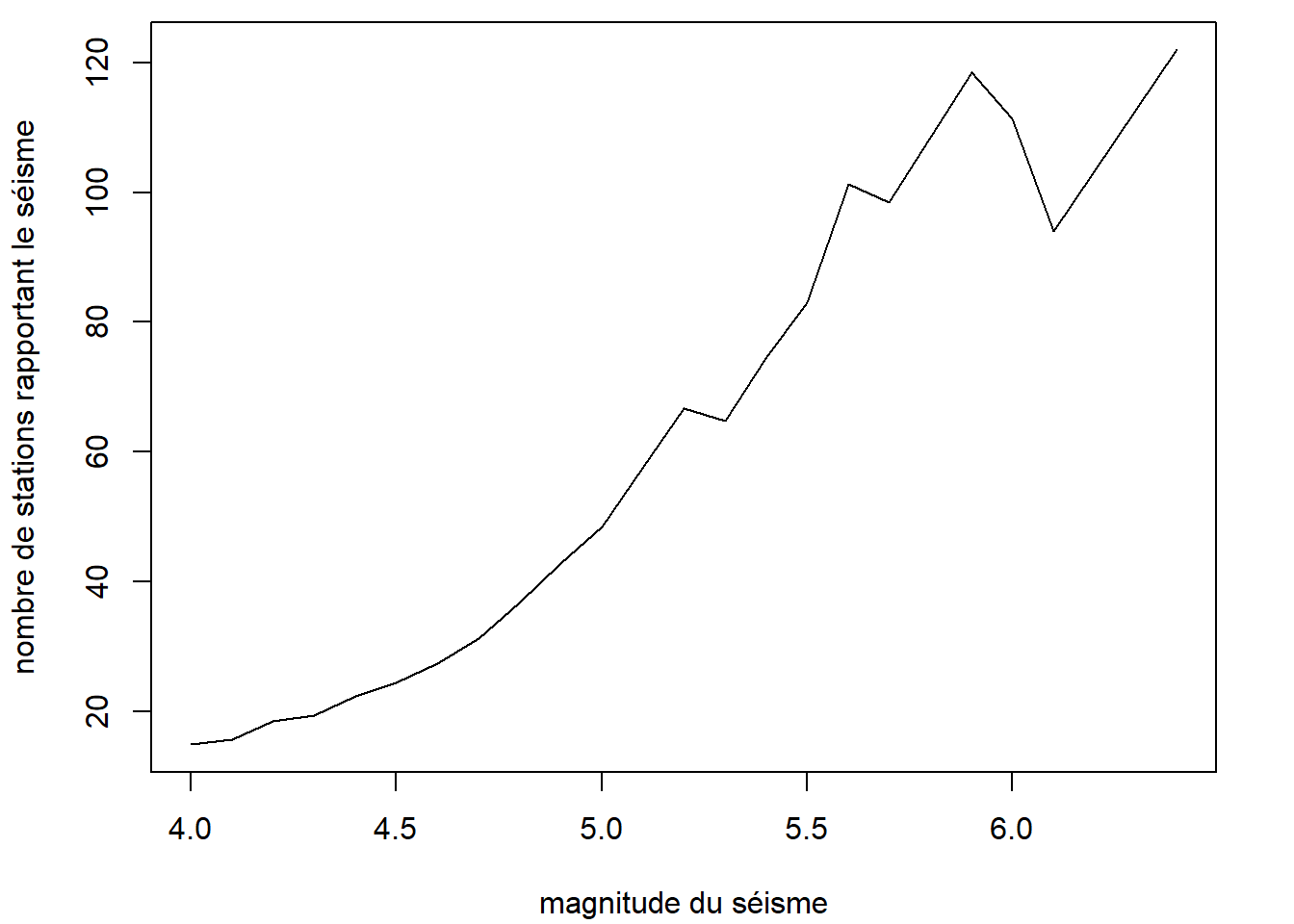
Cet exemple illustre aussi le fait que la fonction plot accepte en entrée une formule.
2.3.3 Diagramme en secteurs - fonction pie
La fonction pie permet de créer des diagrammes en secteurs (en anglais pie charts), aussi nommés diagrammes circulaires ou diagrammes en pointes de tarte ou en camembert. Ce type de graphique est à utiliser avec parcimonie. Il y a d’ailleurs une mise en garde concernant l’utilisation de ce type de graphique dans la fiche d’aide de la fonction pie.
Ce qui est reproché au diagramme en secteurs est qu’il difficile pour l’oeil humain de rapidement comparer les aires des secteurs (qui représentent les fréquences). Il est plus facile de comparer des hauteurs de barres. Donc le diagramme à barres serait un meilleur outil pour représenter des fréquences.
Malgré tout, je crois que le diagramme en secteur est utile pour représenter les fréquences d’une variable à peu de modalités, dans le cas où il n’y a pas de fréquences presque égales, comme dans l’exemple suivant.
pie(x = table(quakes$mag_catego), main = "Fréquences des modalités de magnitude de séismes")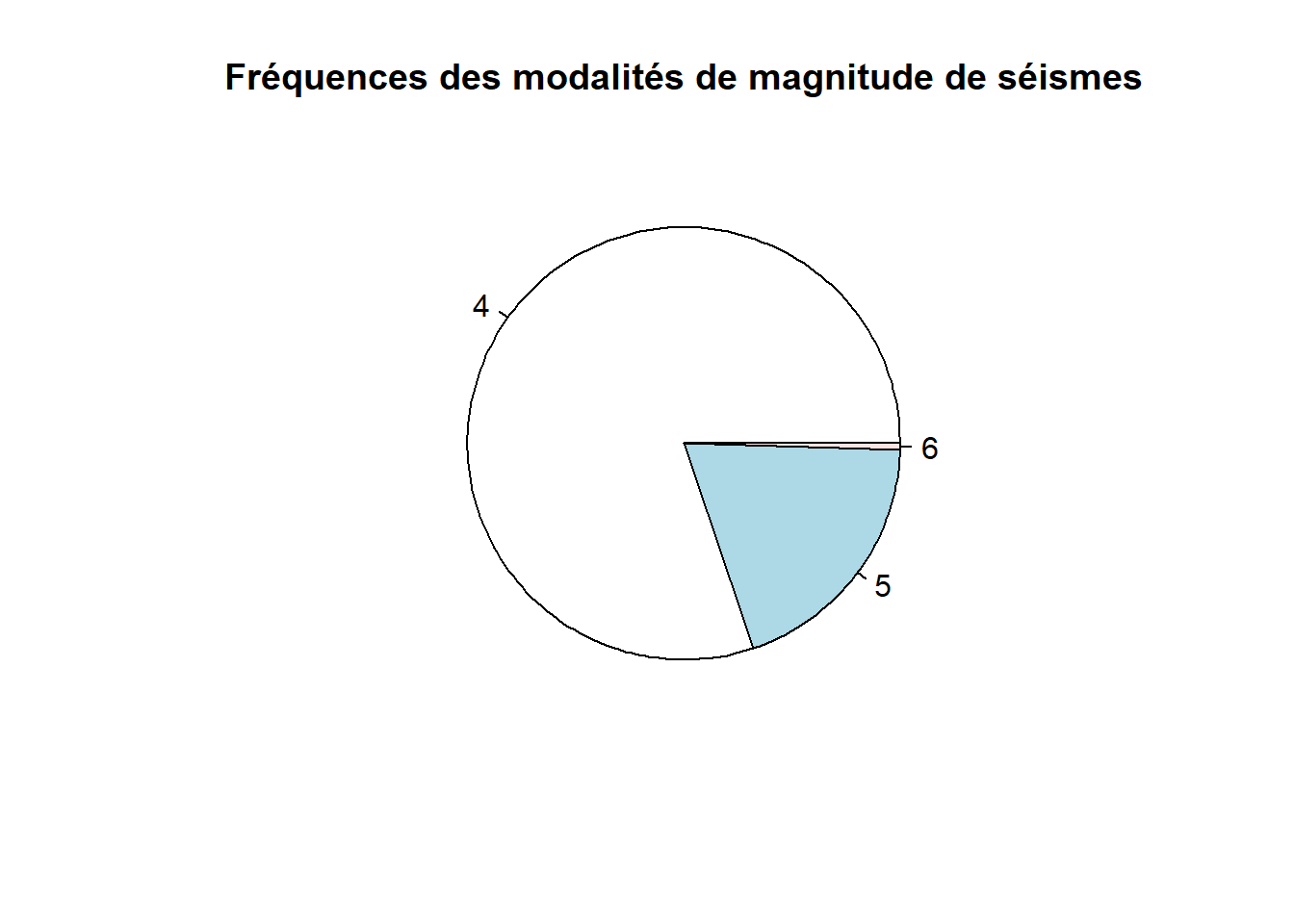
2.3.4 Diagramme à barres - fonction barplot
La fonction barplot produit un diagramme à barres (en anglais bar plot), aussi nommé diagramme en bâtons ou à bandes. Celles-ci peuvent être placées à la verticale (fait par défaut) ou à l’horizontale (argument horiz = TRUE).
barplot(
height = table(quakes$mag_catego),
horiz = TRUE,
xlab = "fréquence",
ylab = "modalité de magnitude"
)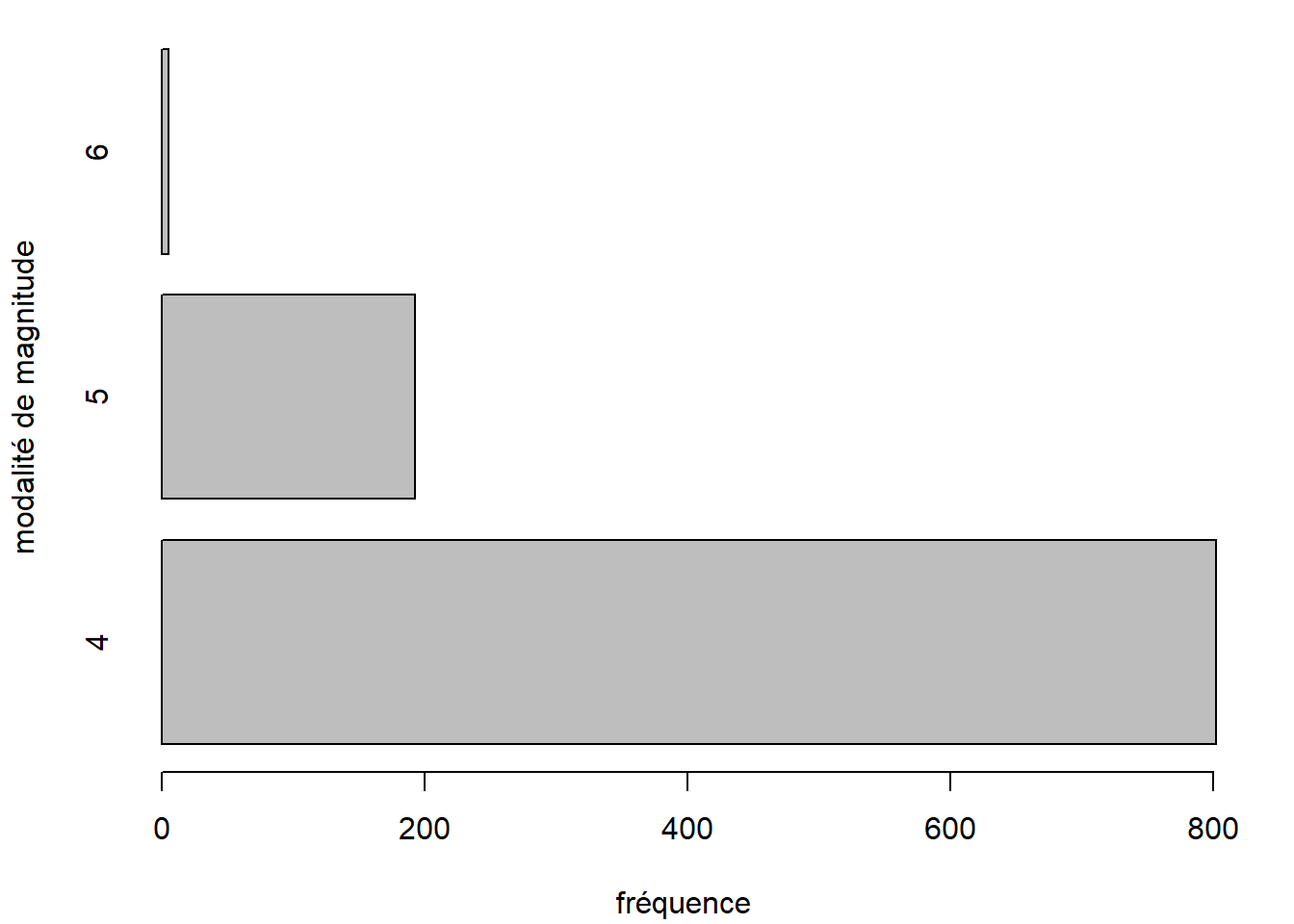
La hauteur des barres dans un diagramme à barres représentent souvent les fréquences des modalités d’une variable catégorique. C’est le cas dans l’exemple précédent. Ces sont ces fréquences qui doivent être fournies à la fonction barplot et non les observations d’origine. Un appel à la fonction barplot est donc souvent accompagné d’une appel à une fonction pour calculer des fréquences comme table ou xtabs.
Pour les graphiques suivants, nous aurons besoin des fréquences des combinaisons de modalités des variables region et mag_catego. Calculons-les tout de suite et stockons les dans un objet.
quakes_freq <- xtabs(~ region + mag_catego, data = quakes)
quakes_freq## mag_catego
## region 4 5 6
## Ouest 151 49 5
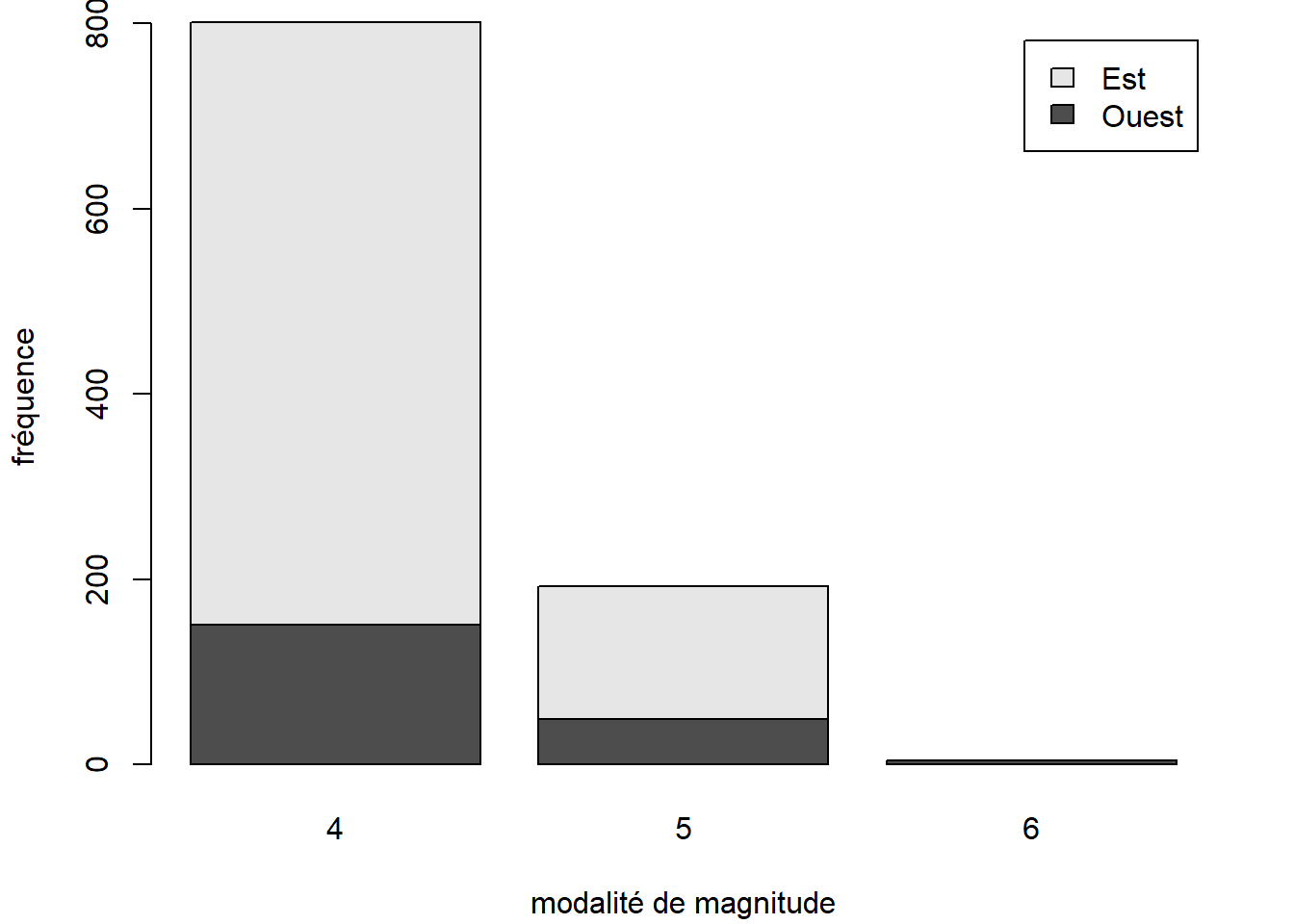
## Est 651 144 0Lorsque qu’un diagramme à barres est utilisé pour représenter des fréquences croisées entre deux variables, les barres pour les différentes variables peuvent être empilés (comportement par défaut de barplot) :
barplot(
height = quakes_freq,
legend.text = TRUE,
xlab = "modalité de magnitude",
ylab = "fréquence"
)
ou groupés (grâce à l’argument beside = TRUE) :
barplot(
height = quakes_freq,
legend.text = TRUE,
beside = TRUE,
xlab = "modalité de magnitude",
ylab = "fréquence"
)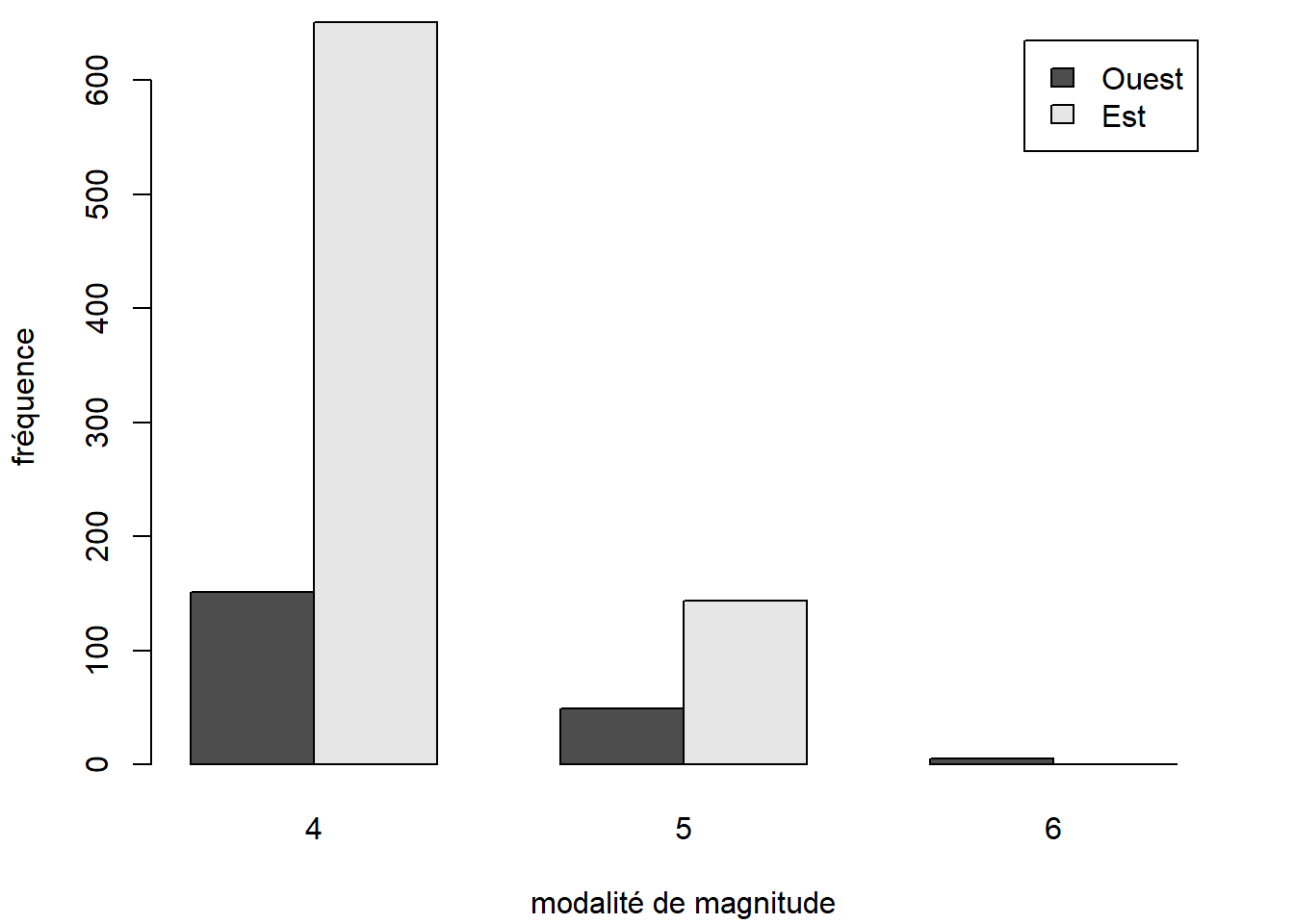
Il est important d’identifier à quelles modalités des variables sont associées les barres. Dans le cas d’un diagramme à barres bivarié, une légende est souvent nécessaire pour ce faire, car l’axe perpendiculaire aux barres ne suffit pas. La fonction barplot peut ajouter une légende au graphique grâce à son argument legend.text.
2.3.5 Diagramme en points de Cleveland - fonction dotchart
Les diagrammes en points de Cleveland (en anglais Cleveland dot plots) peuvent remplacer les diagrammes à barres. Ils offrent une présentation allégée, donc une lisibilité potentiellement accrue dans certaines situations.
dotchart(
x = quakes_freq[2:1, 3:1],
bg = "grey",
xlab = "Fréquence",
ylab = "Région par modalité de magnitude"
)
# L'ordre des lignes et des colonnes de quakes_freq est ajusté pour
# assurer la présentations des fréquences dans l'ordre désiré.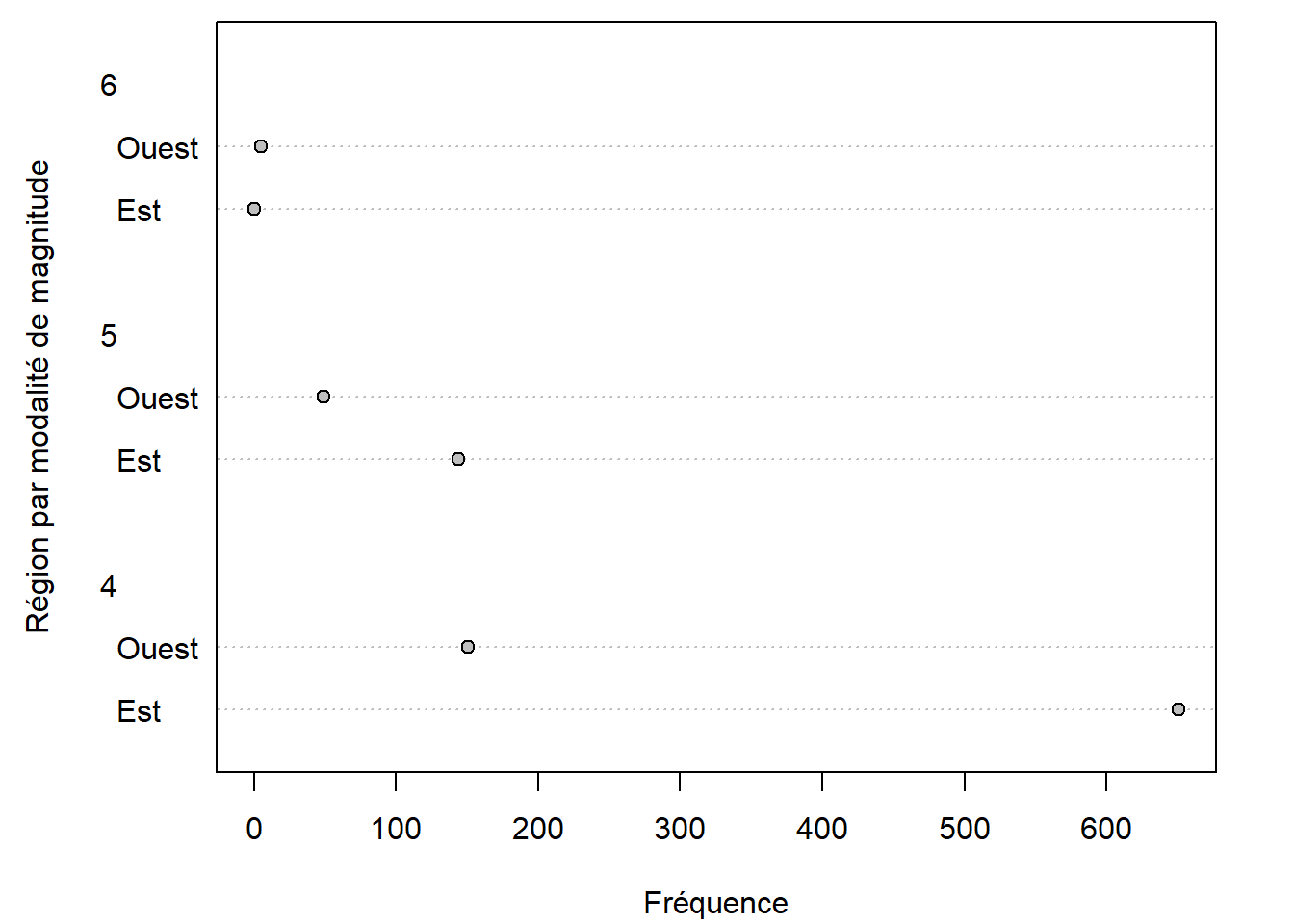
2.3.6 Diagramme en mosaïque - fonction mosaicplot
Une option de rechange au diagramme à barres empilées ou groupées pour représenter des fréquences croisées est le diagramme en mosaïque (en anglais mosaic plot), qui peut être produit avec la fonction mosaicplot.
mosaicplot(
x = quakes_freq[, 3:1],
color = TRUE,
main = "Fréquences croisées",
xlab = "région",
ylab = "modalité de magnitude"
)
# L'ordre des colonnes de quakes_freq est ajusté pour
# assurer la présentations des fréquences dans l'ordre désiré.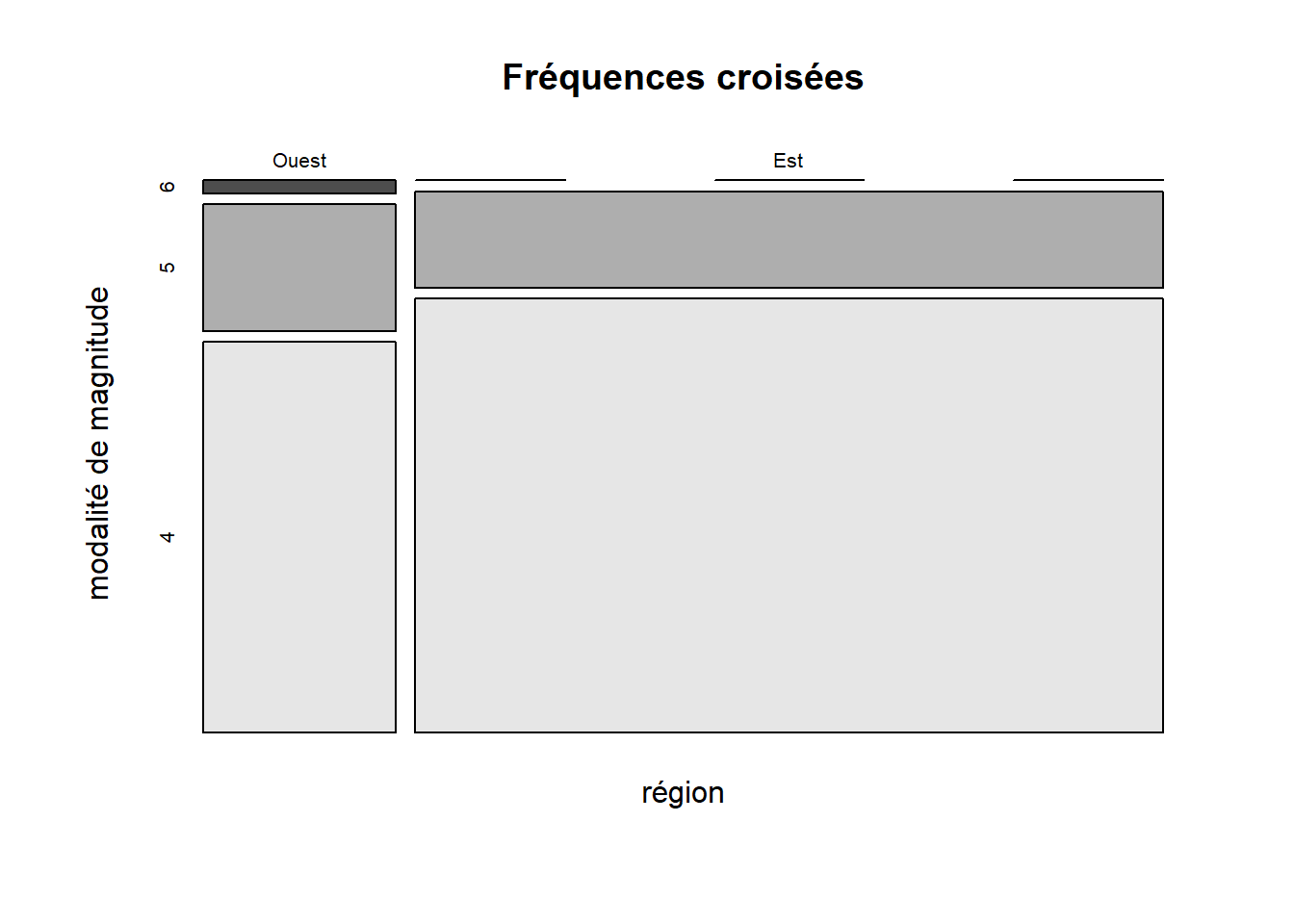
2.3.7 Histogramme - fonction hist
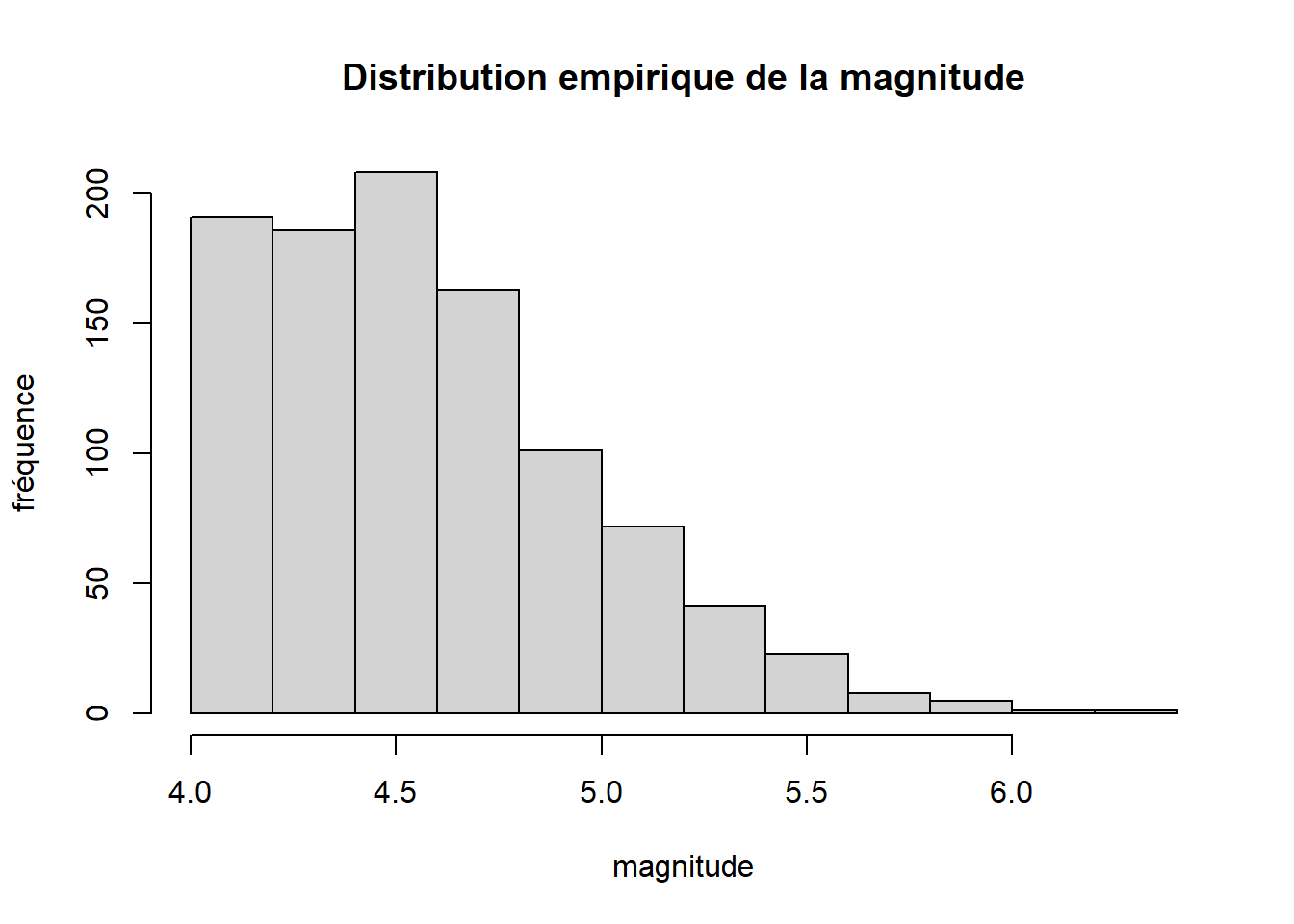
L’histogramme sert à représenter la distribution empirique d’une variable numérique. La fonction hist permet d’en produire.
hist(
x = quakes$mag,
main = "Distribution empirique de la magnitude",
xlab = "magnitude",
ylab = "fréquence"
)
Mine de rien, cette fonction fait beaucoup de travail afin de pouvoir produire un histogramme. Elle commence par briser l’étendue des valeurs de la variable en intervalles disjoints mais contigus, puis elle calcule les fréquences des observations tombant dans les intervalles. Ensuite, elle trace un genre de diagramme à barres en insérant aucun espace entre les barres (puisqu’elles réfèrent à des intervalles contigus). La façon dont les intervalles sont formés peut être contrôlée par les arguments breaks, include.lowest et right. La fonction retourne aussi toutes les statistiques qu’elle calcule, mais il faut accompagner l’appel à la fonction hist d’une assignation pour garder une trace de ces statistiques .
stats <- hist(x = quakes$mag, plot = FALSE)
stats## $breaks
## [1] 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4
##
## $counts
## [1] 191 186 208 163 101 72 41 23 8 5 1 1
##
## $density
## [1] 0.955 0.930 1.040 0.815 0.505 0.360 0.205 0.115 0.040 0.025 0.005 0.005
##
## $mids
## [1] 4.1 4.3 4.5 4.7 4.9 5.1 5.3 5.5 5.7 5.9 6.1 6.3
##
## $xname
## [1] "quakes$mag"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"2.3.8 Diagramme en boîte - fonction boxplot
Un autre graphique conçu pour représenter la distribution empirique d’une variable numérique est le diagramme en boîte (en anglais boxplot), aussi appelé boîte à moustaches ou diagramme de quartiles. Ce type de graphique peut être produit en R avec la fonction boxplot.
boxplot(x = quakes$mag, ylab = "magnitude")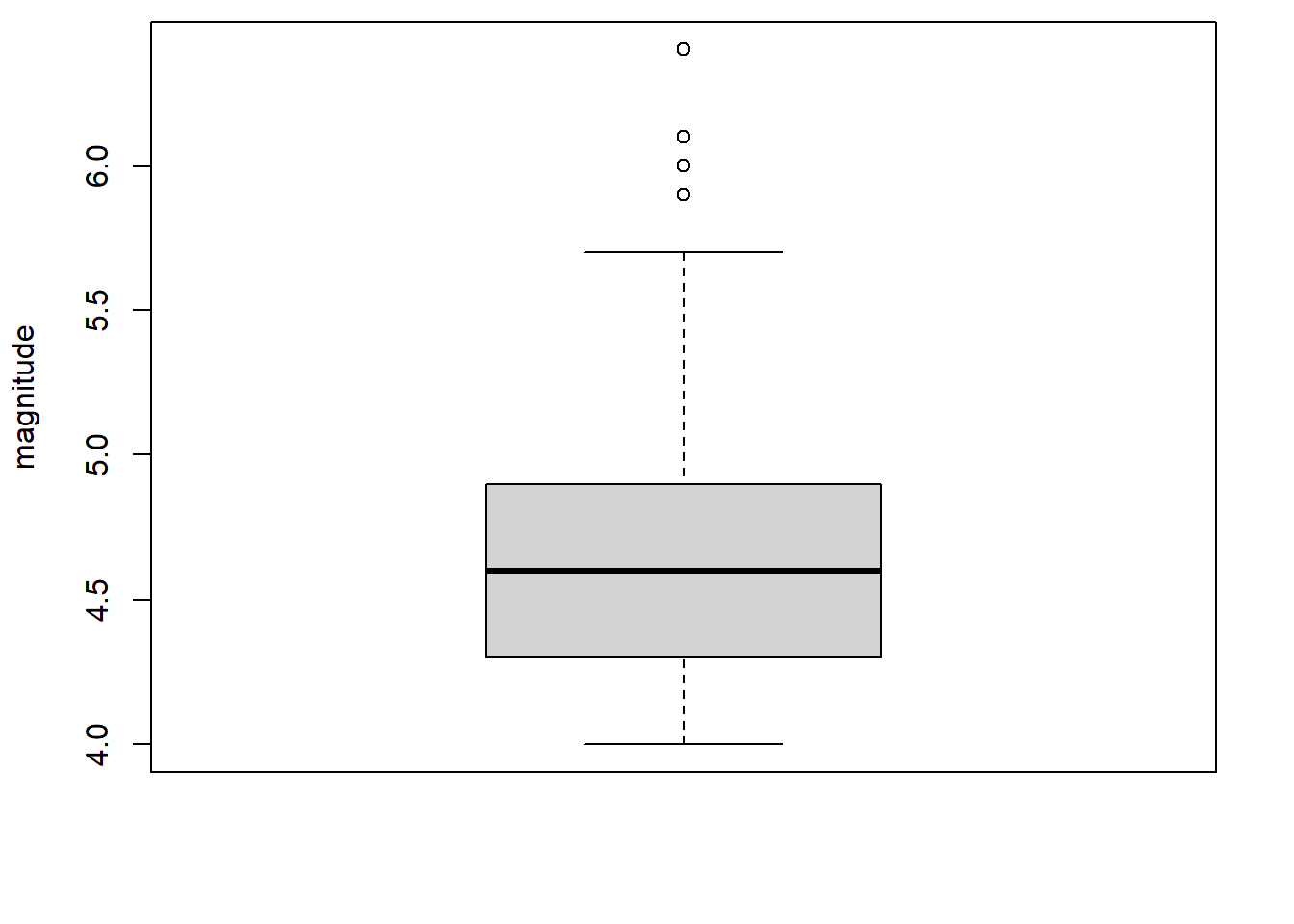
L’association entre une variable numérique et une variable catégorique peut être représentée par des diagrammes en boîtes juxtaposés.
boxplot(mag ~ region, data = quakes, xlab = "région", ylab = "magnitude")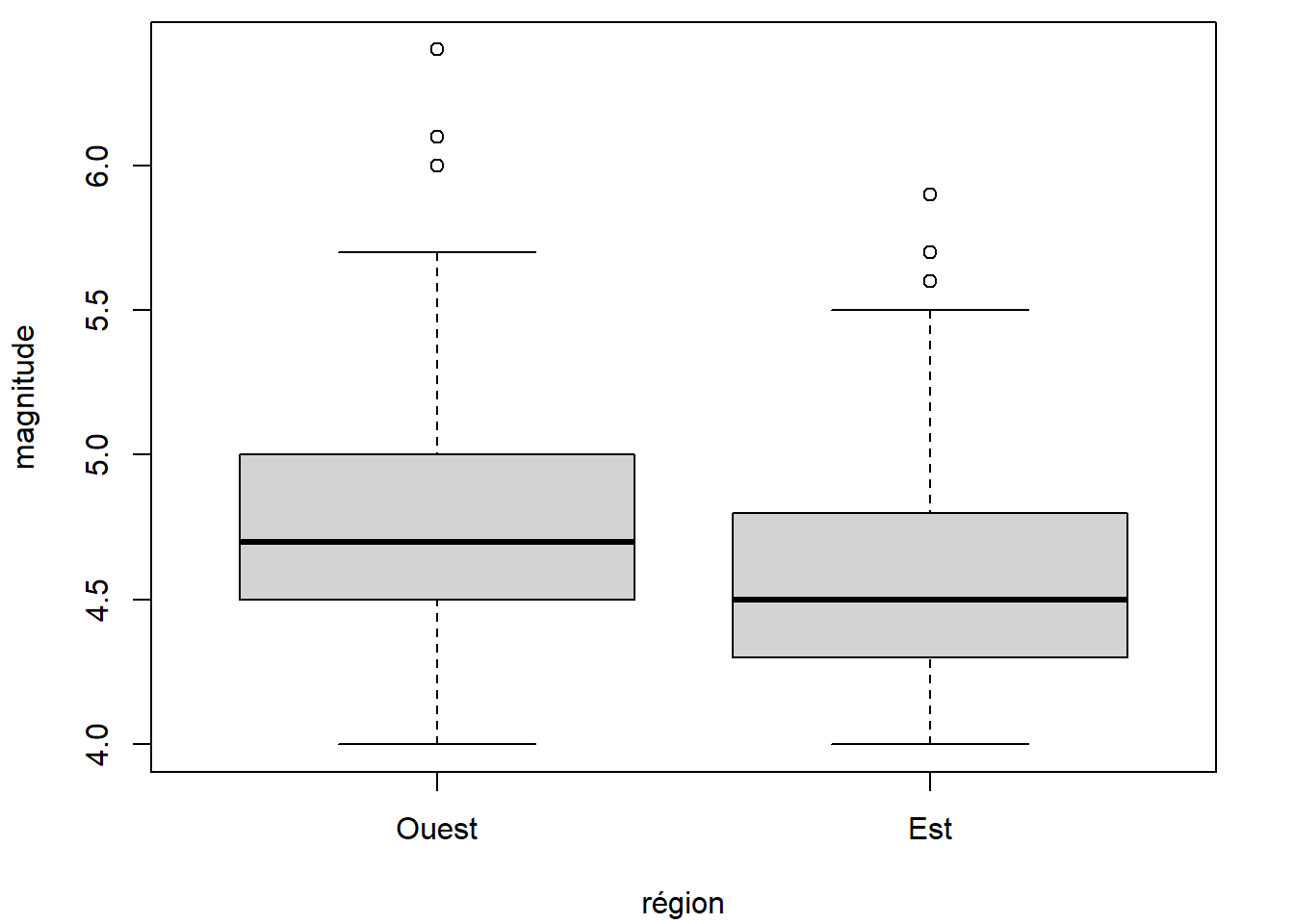
Par exemple, pour produire des diagrammes en boîtes pour les observations de la variable numérique mag en fonction de la variable catégorique region, la fonction boxplot peut être appelée en lui fournissant en entrée une formule contenant dans sa partie de droite la variable numérique et dans sa partie de gauche la variable catégorique.
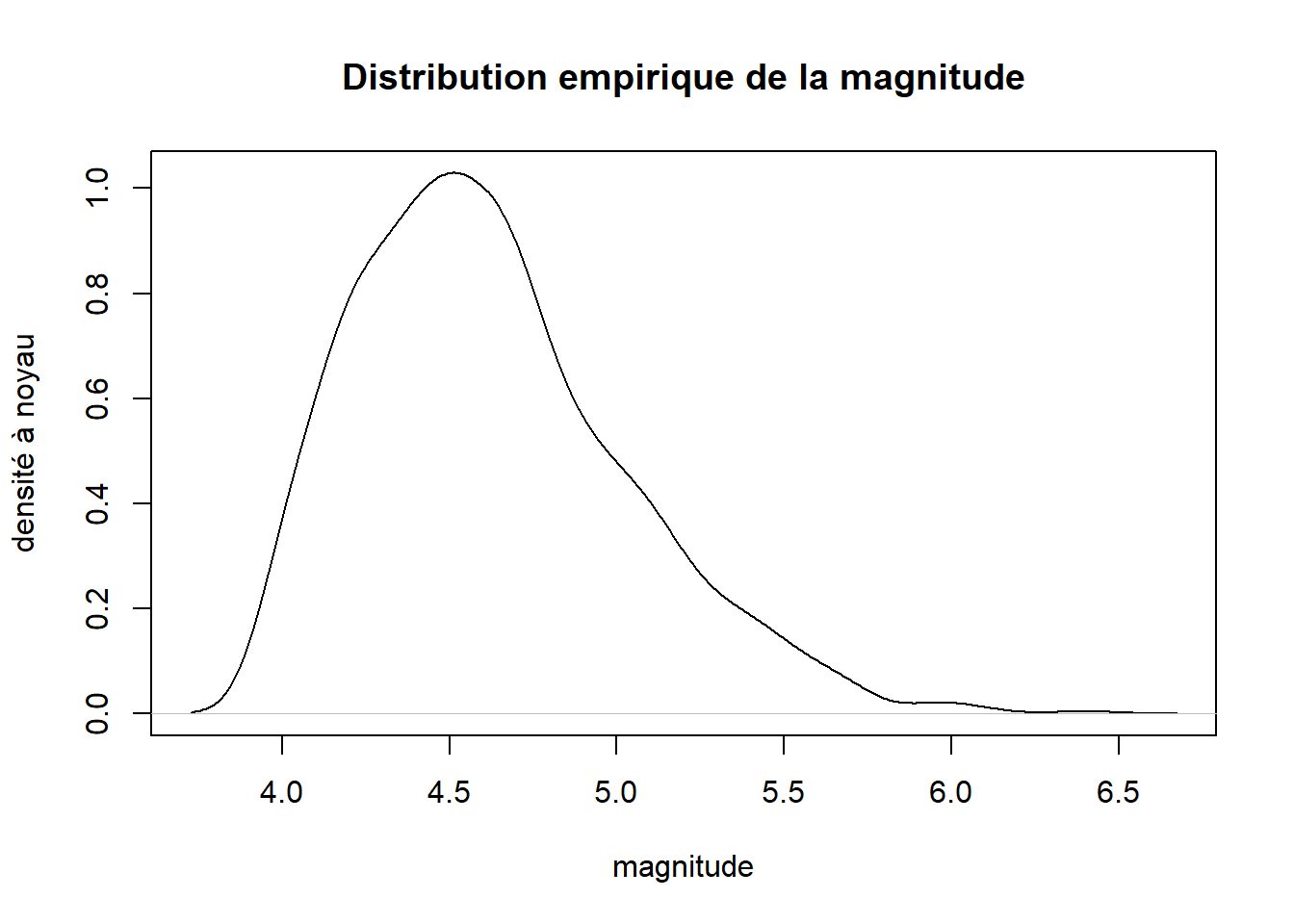
2.3.9 Courbe d’estimation de densité à noyau - méthode plot.density
La fonction density estime une densité empirique par la méthode à noyau (en anglais Kernel density estimation) à partir des observations d’une variable numérique. Une représentation graphique de cette densité empirique avec la méthode plot.density (via la fonction générique plot ou directement) est une autre alternative pour visualiser les observations d’une variable numérique.
plot(
x = density(quakes$mag),
main = "Distribution empirique de la magnitude",
xlab = "magnitude",
ylab = "densité à noyau"
)
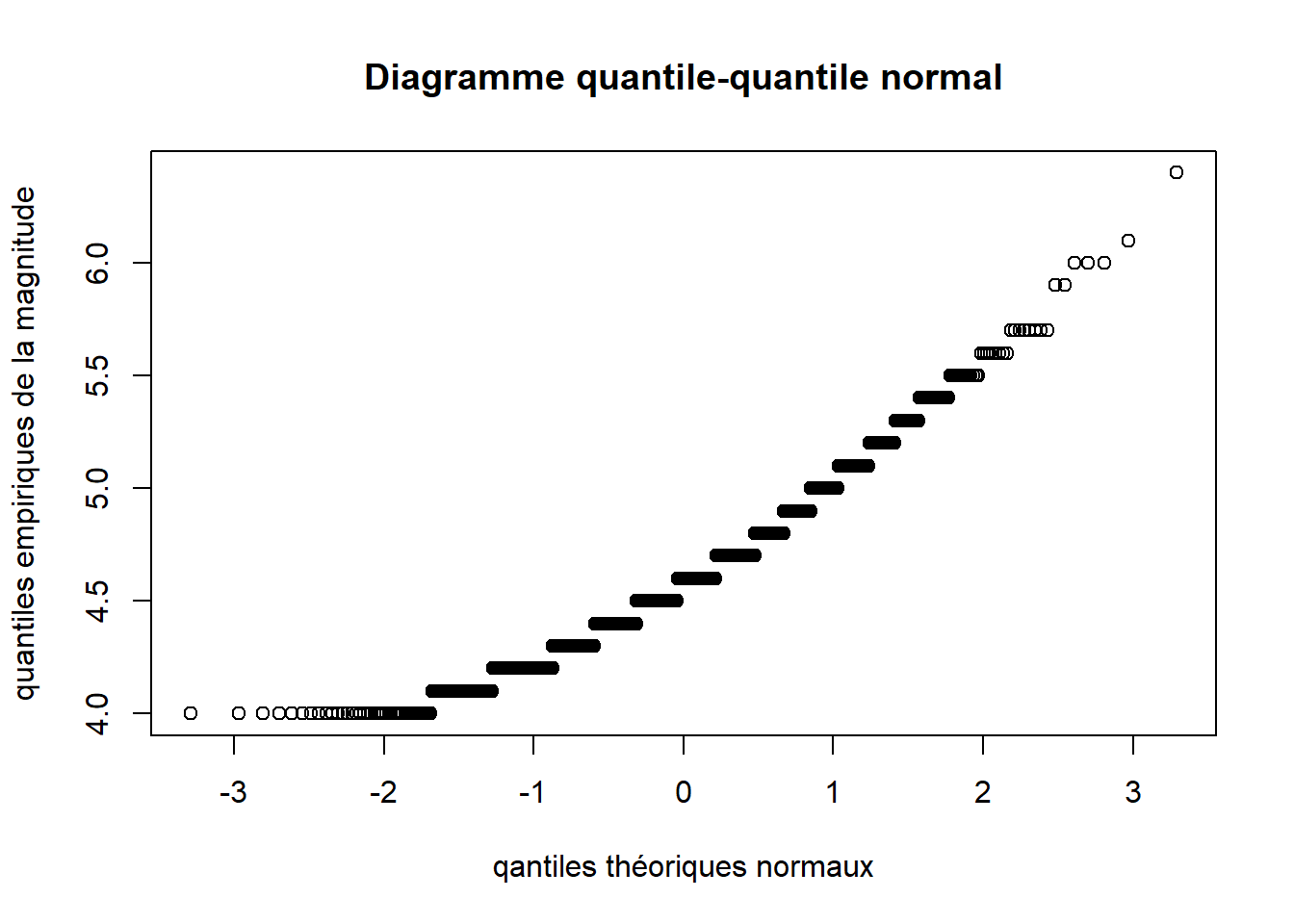
2.3.10 Diagramme quantile-quantile - fonctions qqnorm et qqplot
Les diagrammes quantile-quantile (en anglais Q-Q plot) servent à comparer des distributions. Le plus connus des diagrammes quantile-quantile est probablement le diagramme quantile-quantile théorique normal qui permet de comparer une distribution empirique à une distribution théorique normale. Ce type de graphique peut être produit en R avec la fonction qqnorm.
qqnorm(
y = quakes$mag,
main = "Diagramme quantile-quantile normal",
xlab = "qantiles théoriques normaux",
ylab = "quantiles empiriques de la magnitude"
)
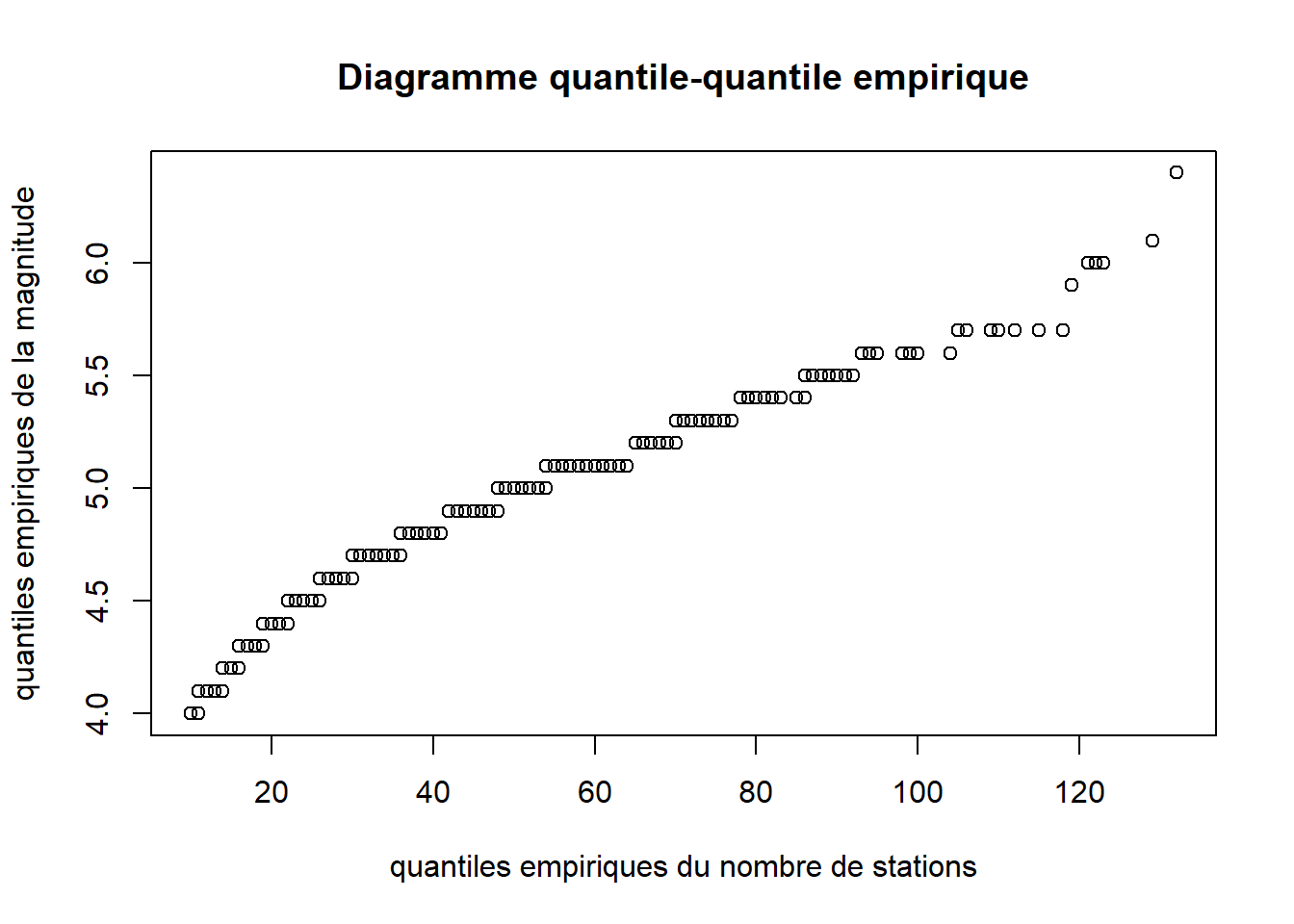
Les diagrammes quantile-quantile empiriques servent quant à eux à comparer deux distributions empiriques. La fonction qqplot permet d’en produire.
qqplot(
x = quakes$stations, y = quakes$mag,
main = "Diagramme quantile-quantile empirique",
xlab = "quantiles empiriques du nombre de stations",
ylab = "quantiles empiriques de la magnitude"
)
2.3.11 Représentation graphique d’une expression mathématique - fonction curve
La représentation graphique d’une fonction mathématique est possible en R avec la fonction curve.
curve(expr = log)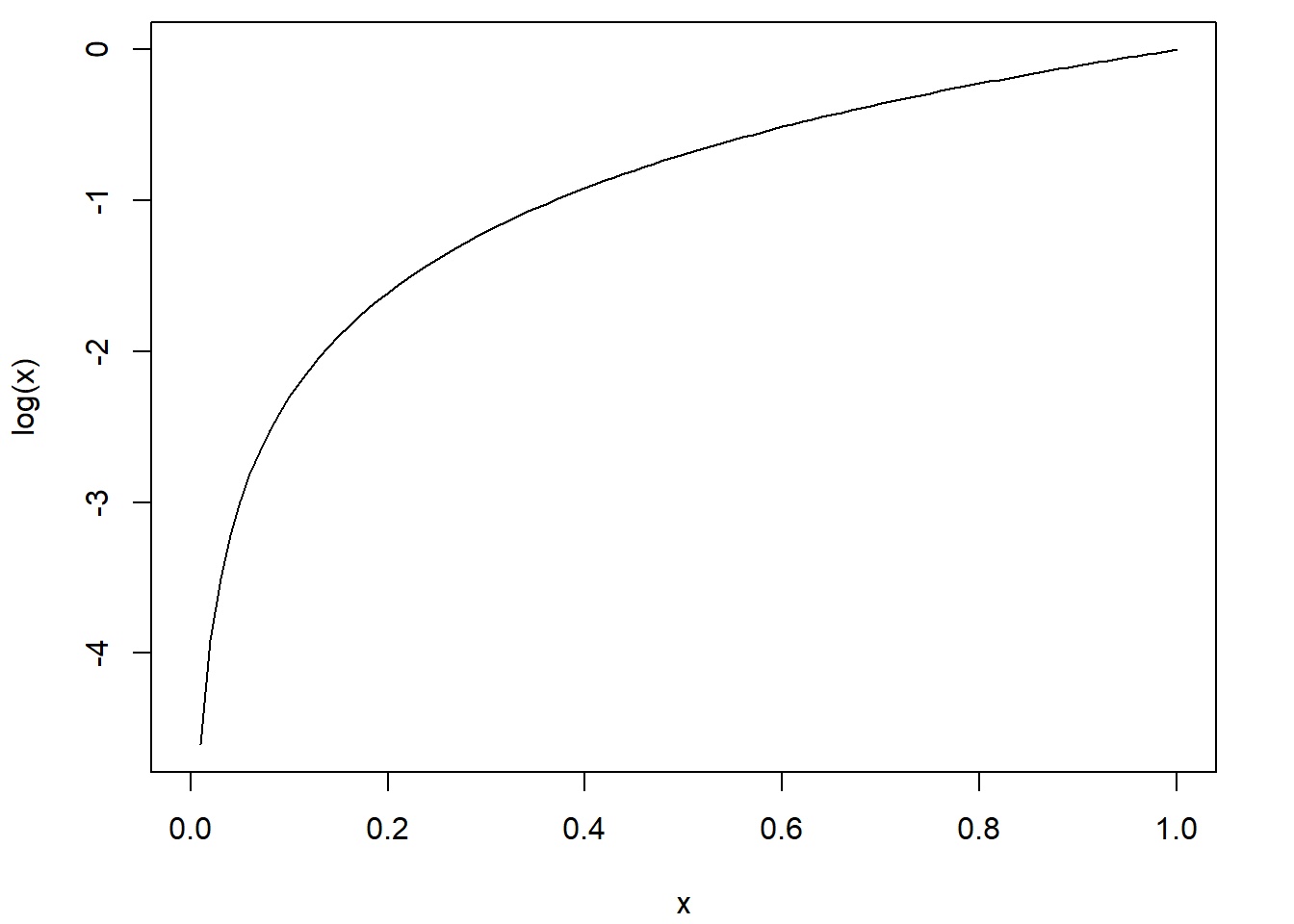
Par défaut, la fonction curve fait une évaluation de la valeur de la fonction en 101 points également répartis entre 0 et 1. Il est possible de modifier ces points grâce aux arguments from, to et n (une séquence de points est créée avec la fonction seq). De plus, le premier argument n’est pas contraint à être une fonction. Il peut s’agir de n’importe quelle expression écrite comme une fonction de x.
curve(expr = x^2 + 5*x - 25, from = -23, to = 18, n = 200)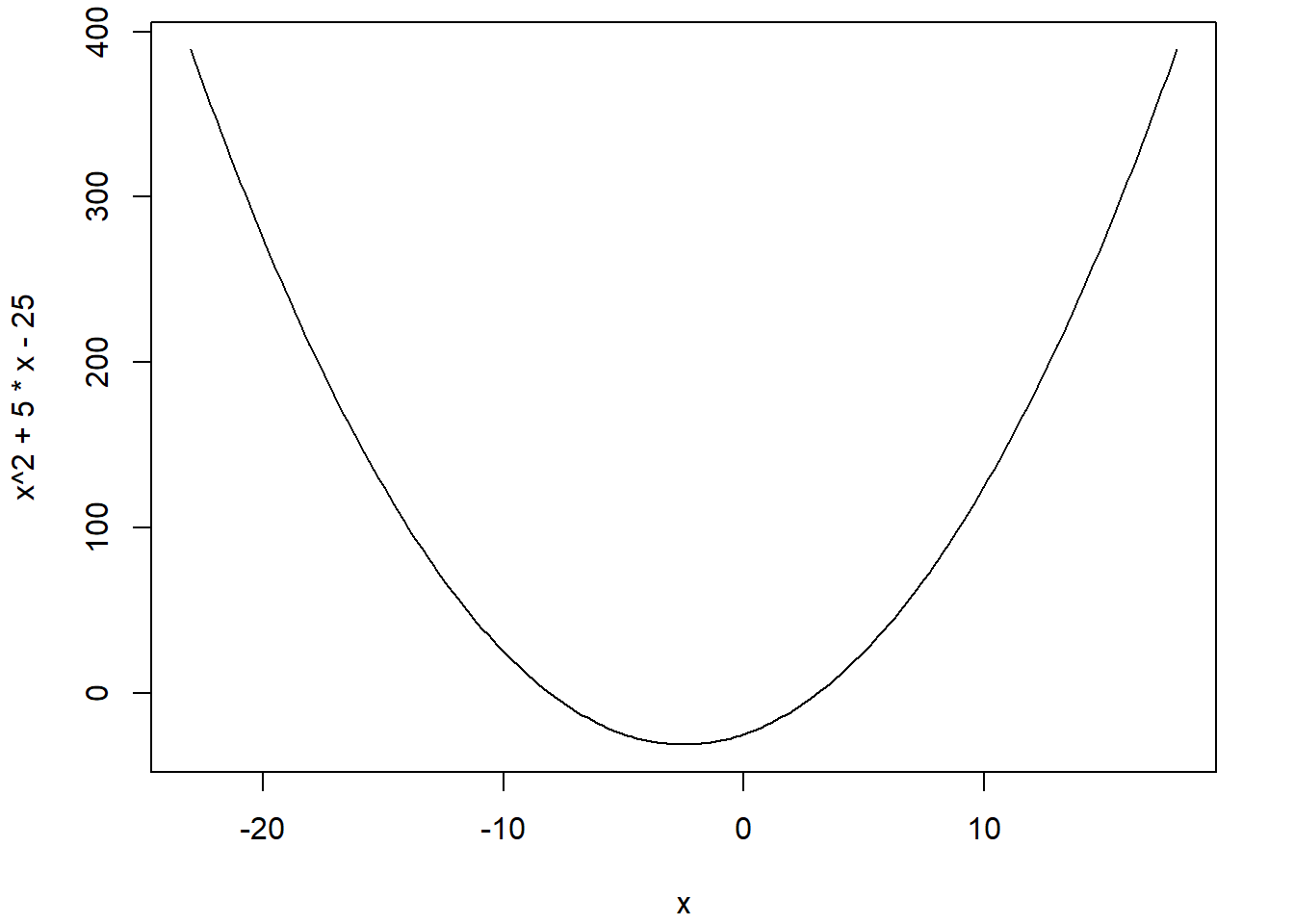
Le code suivant produit le même graphique, mais l’utilisation de la fonction curve crée une commande plus succincte.
x <- seq(from = -23, to = 18, length = 200)
plot(x = x, y = x^2 + 5*x - 25, type = "l")2.4 Modification de l’ordre des niveaux d’un facteur
Lorsqu’un facteur est représenté dans un graphique, ses niveaux (ou modalités) sont présentés en respectant leur ordre dans les attributs (métadonnées) du facteur. Par exemple, dans les diagrammes en boîtes juxtaposés créés précédemment (et repris ci-dessous), le niveau Ouest du facteur region de quakes est présenté avant le niveau Est (même si selon l’ordre alphabétique, Est vient avant Ouest).
boxplot(mag ~ region, data = quakes, xlab = "région", ylab = "magnitude")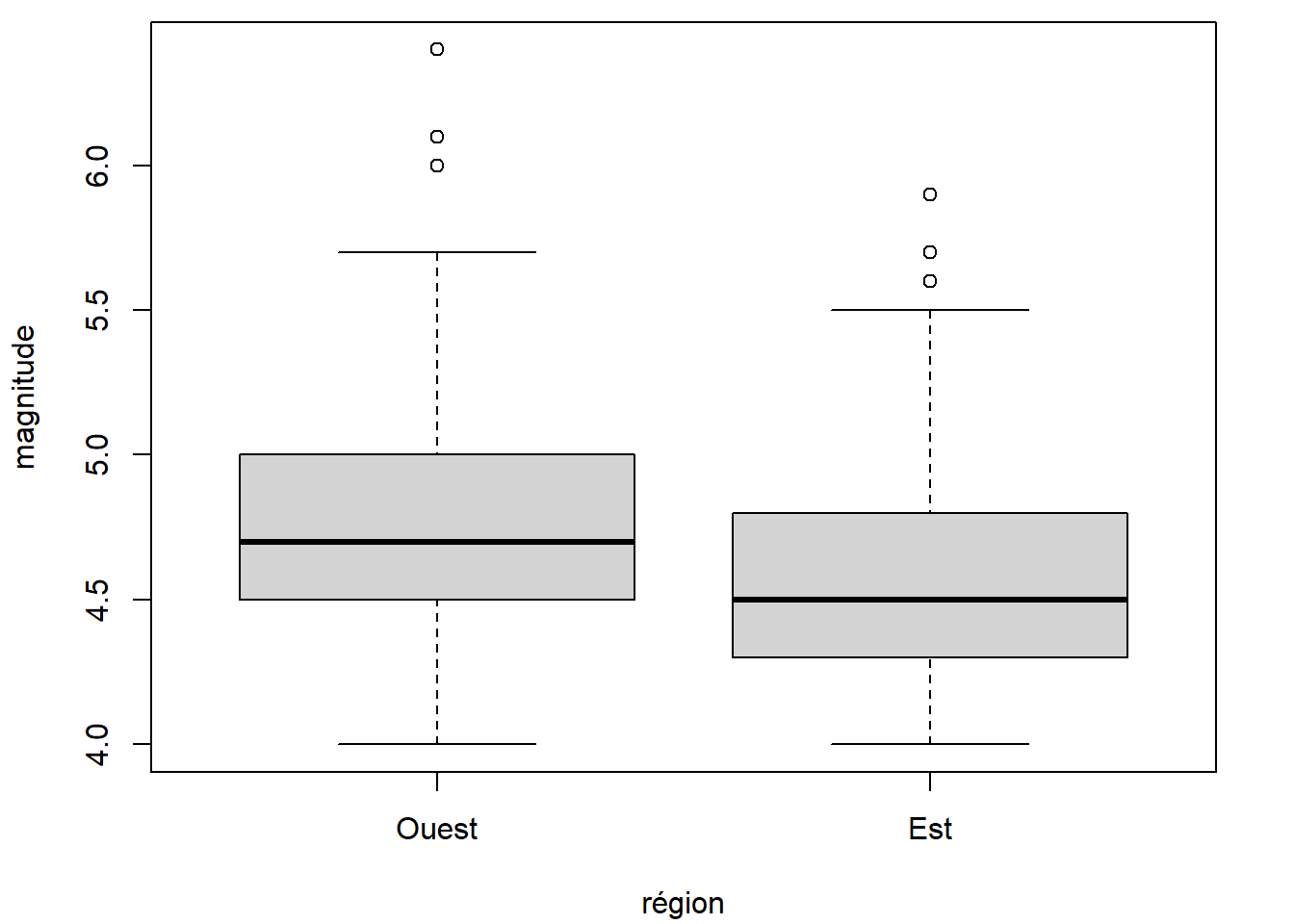
Cet ordre est utilisé, car il s’agit de l’ordre officiel des niveaux de ce facteur.
levels(quakes$region)## [1] "Ouest" "Est"Si nous voulions voir apparaître dans le graphique les niveaux du facteur dans un autre ordre, il faudrait aller modifier les attributs du facteur, comme nous avons appris à le faire dans les notes sur les structures de données en R. Voici un exemple.
quakes_modif <- quakes
quakes_modif$region <- factor(quakes_modif$region, levels = c("Est", "Ouest"))
boxplot(mag ~ region, data = quakes_modif, xlab = "région", ylab = "magnitude")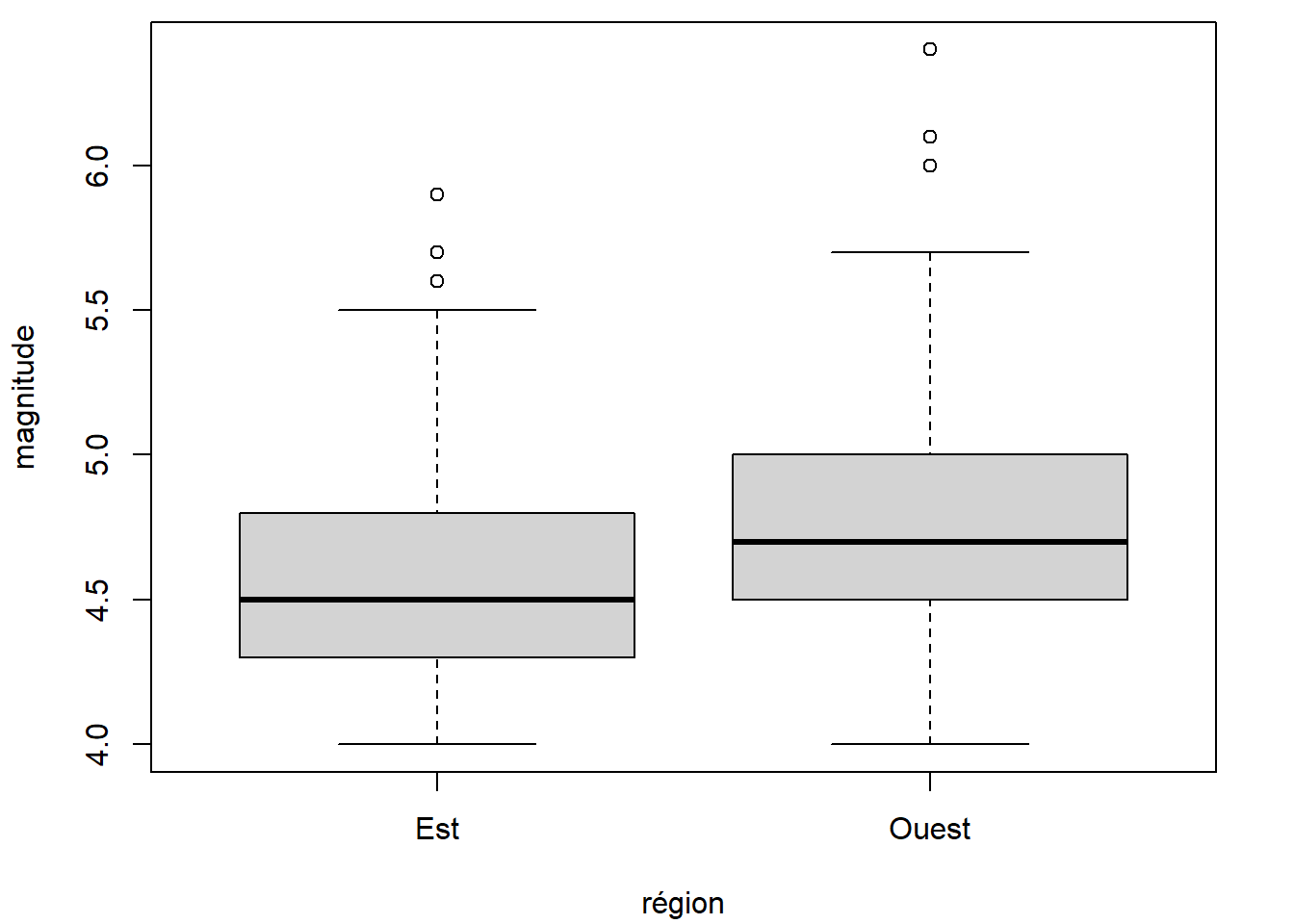
2.5 Arguments et paramètres graphiques
Les fonctions vues jusqu’à présent possèdent toutes des arguments pour contrôler la mise en forme et les annotations des graphiques. La liste complète de ces arguments varient d’une fonctions à l’autre, mais certains arguments sont communs à presque toutes les fonctions graphiques. Nous allons voir ici les arguments les plus utiles.
Les arguments permettant de contrôler la mise en forme sont appelés paramètres graphiques. La plupart peuvent être spécifiés soit dans l’appel à la fonction graphique, soit dans un appel à la fonction par. Par contre, certains paramètres graphiques peuvent uniquement être fixés avec par.
Un paramètre graphique fourni dans un appel à une fonction graphique est effectif seulement pour le graphique produit, alors qu’un paramètre graphique fourni dans un appel à par reste effectif jusqu’à ce que nous le modifions de nouveau. Alors, avant de modifier des paramètres graphiques avec par, il est bon d’enregistrer les valeurs par défaut des paramètres, comme suit,
all_par_default <- par(no.readonly = TRUE)afin de pouvoir facilement réattribuer ces valeurs par défaut aux paramètres, comme suit,
par(all_par_default)à la fin des nos commandes pour produire un graphique. L’objet all_par_default est une liste contenant les valeurs par défaut de tous les paramètres graphiques modifiables. Il est aussi possible d’enregistrer seulement les valeurs des paramètres graphiques modifiés par un appel à la fonction par en l’accompagnant d’une assignation. Les valeurs enregistrées sont celles que prenaient les paramètres avant d’être modifiés. Par exemple, l’objet par_default obtenu ainsi :
par_default <- par(mar = c(1, 1, 2, 1))contient uniquement la valeur par défaut du paramètre mar.
par_default## $mar
## [1] 5.1 4.1 4.1 2.1La valeur initiale du paramètre mar est réactivée comme suit.
par(par_default)Notons que les changements apportés aux paramètres graphiques ne sont pas conservés lors de la fermeture de la session R. À l’ouverture d’une session R, les paramètres graphiques prennent donc toujours leurs valeurs par défaut.
Voici deux tableaux résumant les arguments et paramètres graphiques les plus communs :
| Arguments | Éléments graphiques contrôlés |
|---|---|
main |
titre |
sub |
note en bas de page |
xlab, ylab |
noms des axes |
xlim, ylim |
étendue des axes |
type |
type de représentation ("p" = points, "l" = lignes, "b" = les deux, etc.) |
| Paramètres | Éléments graphiques contrôlés |
|---|---|
ann |
si FALSE, retire le titre et les noms d’axes |
bty |
si "n", retire le cadre autour de la zone graphique |
(autres valeurs acceptées : "o", "l", "7", "c", "u" et "]") |
|
lwd |
épaisseur des lignes |
lty |
type des lignes |
pch |
symbole pour les points |
las |
orientation des étiquettes des axes |
(0 = parallèle à l’axe, 1 = horizontale, 2 = perpendiculaire à l’axe, 3 = verticale) |
|
font |
type de police de caractères dans la zone graphique, |
(1 = normal, 2 = gras, 3 = italique, etc.) |
|
font.main, font.sub, |
dans le titre, dans la note en bas de page, |
font.axis, font.lab |
dans les étiquettes des axes, dans les noms des axes |
family |
famille de police de caractères |
("serif", "sans", "mono", "symbol", etc., plus de choix avec le package showtext) |
|
cex |
taille des caractères dans la zone graphique, |
cex.main, cex.sub, |
dans le titre, dans la note en bas de page, |
cex.axis, cex.lab |
dans les étiquettes des axes, dans les noms des axes |
col |
couleur des éléments de la zone graphique, |
col.main, col.sub, |
du titre, de la note en bas de page, |
col.axis, col.lab |
des étiquettes des axes, des noms des axes |
bg |
couleur de l’intérieur du symbole pour les points lorsque pch prend une valeur entre 21 et 25 (pas la même signification dans par) |
par(mfrow = c( , )) |
division de la fenêtre graphique |
par(mfcol = c( , )) |
|
par(new = TRUE) |
superposition de graphiques |
par(mar = c( , , , )) |
tailles des marges |
par(oma = c( , , , )) |
tailles des marges externes (par défaut nulles) |
La liste de tous les paramètres graphiques R est bien plus longue que ça. Il en existe plus de soixante-dix, tous documentés dans la fiche d’aide de la fonction par.
L’utilisation de certains de ces arguments a déjà été illustré dans les exemples précédents. Voici un exemple supplémentaire dans lequel quelques éléments de la mise en forme sont modifiés dans le diagramme de dispersion de la variable stations en fonction de la variable mag
plot(
x = quakes$mag,
y = quakes$stations,
main = "1000 séismes près de Fidji",
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme",
font.lab = 3, # nom d'axes en italique
font.main = 4, # titre en gras italique
cex.axis = 0.8, # étiquettes des axes plus petites
bty = "n" # pas de cadre autour de la zone graphique
)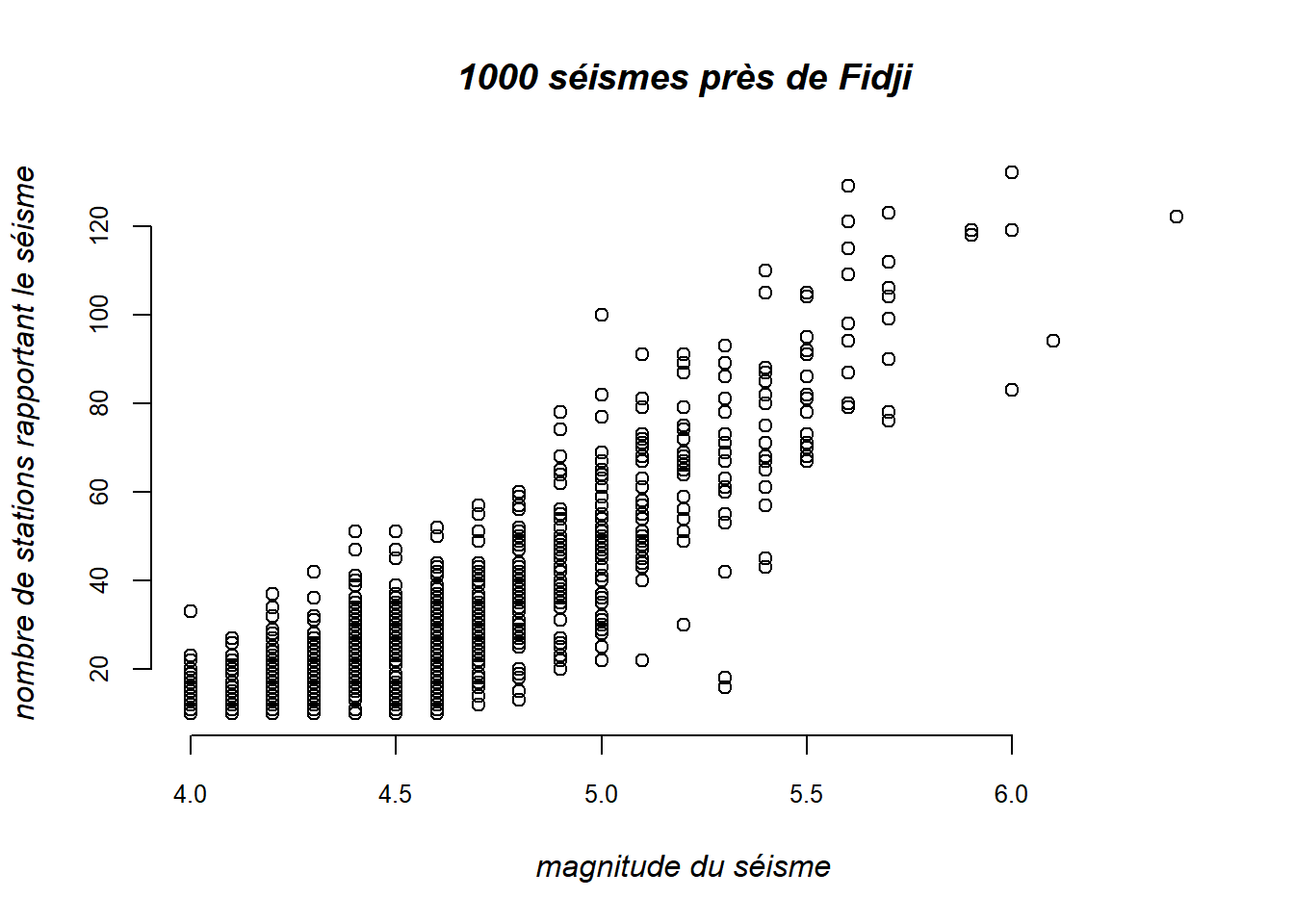
Remarquons que les accents ne causent pas de problèmes dans le titre et les noms d’axes.
Nous pouvons aussi modifier certains paramètres graphiques par un appel à la fonction par comme suit.
par_default <- par(font.lab = 3, font.main = 4, cex.axis = 0.8, bty="n")
plot(
x = quakes$mag, y = quakes$stations,
main = "1000 séismes près de Fidji",
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
par(par_default)Utiliser la fonction par est pratique si nous avons plusieurs graphiques à produire avec les mêmes paramètres.
Types de représentation - argument type
Voici un graphique qui représente toutes les valeurs que peut prendre l’argument type.
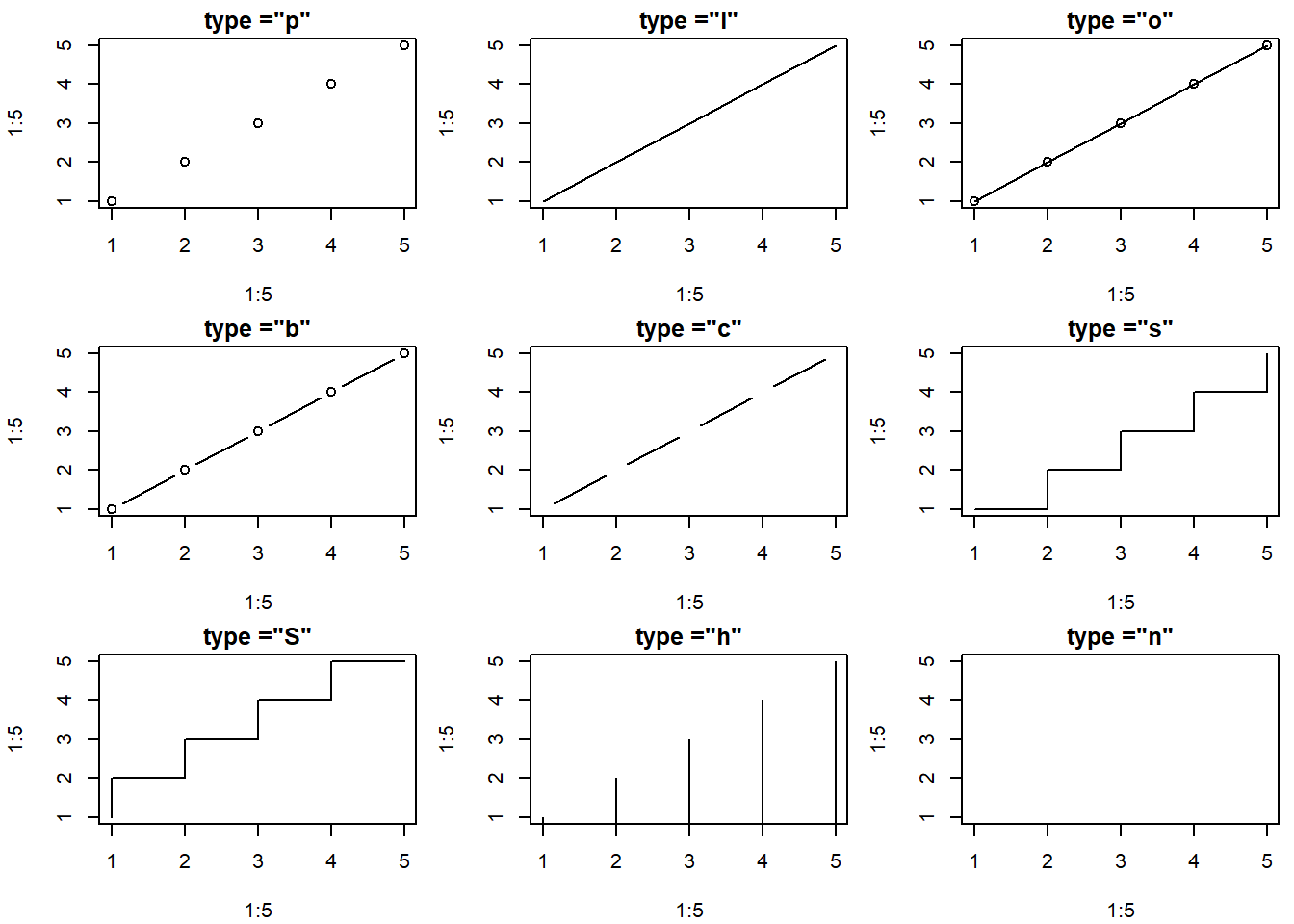
Ce graphique est une adaptation d’un graphique sur la page web suivante :
http://www.statmethods.net/graphs/line.html.
Types de lignes - paramètre lty
Voici un graphique qui représente toutes les valeurs que peut prendre le paramètre lty.
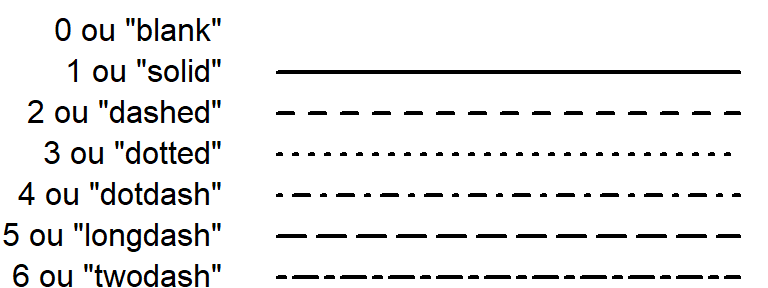
Ce graphique est une adaptation d’un graphique sur la page web suivante :
http://www.sthda.com/french/wiki/les-differents-types-de-traits-dans-r-lty
Symboles pour les points - paramètre pch
Voici un graphique qui représente toutes les valeurs numériques que peut prendre le paramètre pch. Ce paramètre accepte aussi comme valeur un caractère quelconque.

Ce graphique est une adaptation d’un graphique sur la page web suivante :
http://www.sthda.com/french/wiki/les-differents-types-de-points-dans-r-comment-utiliser-pch
2.5.1 Couleurs
Une couleur peut être spécifiée de différentes façons :
- par une chaîne de caractère contenant un nom de couleur,
- par une chaîne de caractères hexadécimaux de la forme
"#rrggbb"ou"#rrggbbaa", - par un nombre entier référant à une palette de couleur.
Nom de couleur
La commande suivante affiche tous les noms de couleurs compris par R.
colors()## [1] "white" "aliceblue" "antiquewhite" "antiquewhite1" "antiquewhite2"
## [6] "antiquewhite3" "antiquewhite4" "aquamarine" "aquamarine1" "aquamarine2"
## [11] "aquamarine3" "aquamarine4" "azure" "azure1" "azure2"
## [ reached getOption("max.print") -- omitted 642 entries ]Il y en a 657 (seulement les 15 premiers sont affichés ici). Certains de ces noms sont plutôt originaux, par exemple "lemon chiffon", "peach puff" et "papaya whip" [4]! Ces couleurs sont représentées dans le graphique suivant, selon la position de la couleur dans le vecteur retourné par la commande colors().
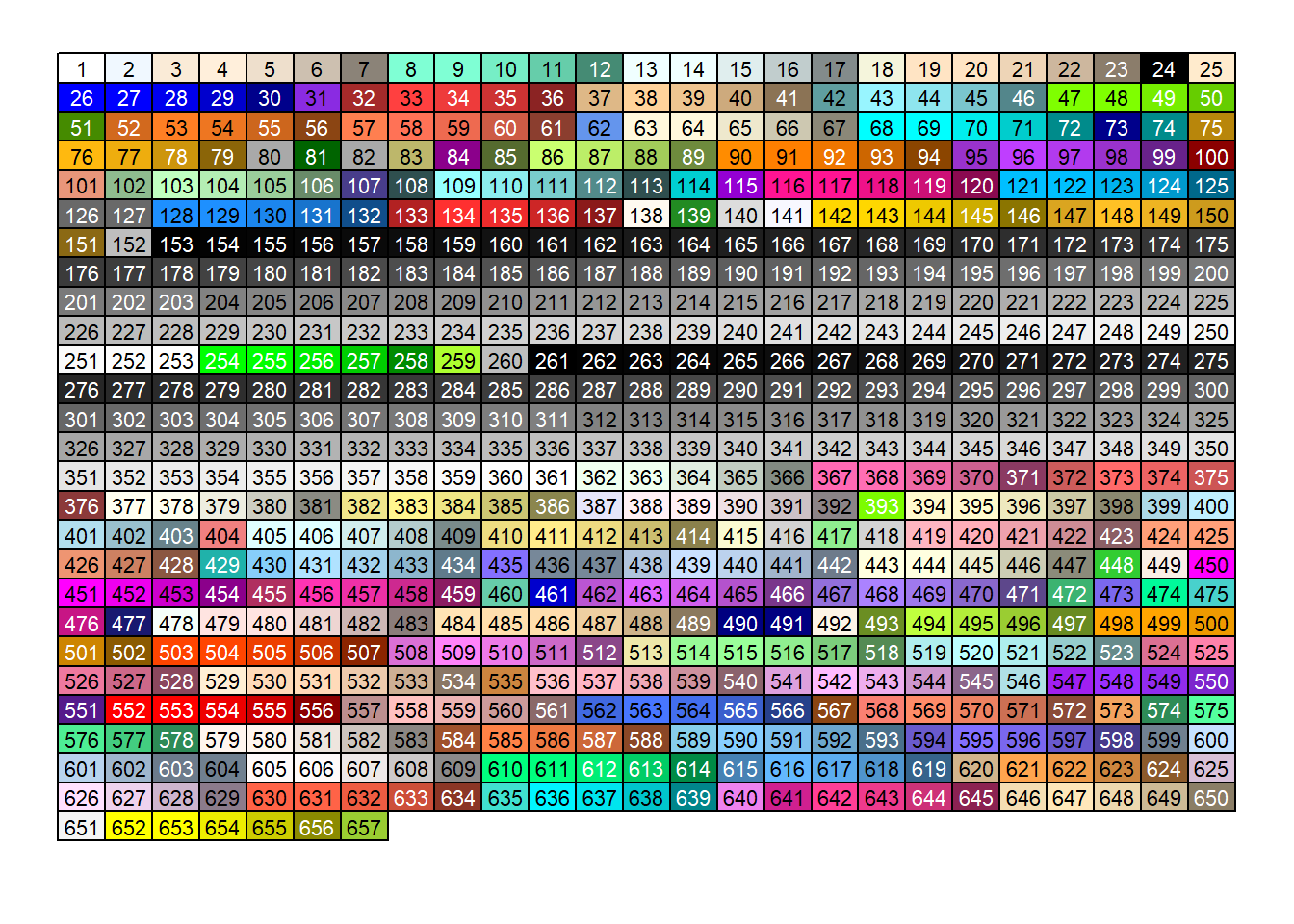
Ce graphique a été produit grâce à un code R partagé sur la page web suivante :
https://github.com/EarlGlynn/colorchart/wiki/Color-Chart-in-R
Chaîne de caractères hexadécimaux de la forme "#rrggbb" ou "#rrggbbaa"
Dans une chaîne de caractères hexadécimaux de la forme "#rrggbb" ou "#rrggbbaa", les paires des caractères rr, gg, bb et aa sont des digits hexadécimaux spécifiant une valeur entre 00 (minimum) et FF (maximum). Ces digits indiquent respectivement un niveau de rouge, de vert, de bleu et d’opacité. Le niveau d’opacité est facultatif. Par défaut les couleurs sont complètement opaques. Une valeur d’opacité minimale 00 représente une transparence complète et une valeur d’opacité maximale FF représente une opacité complète.
Pour déterminer un code hexadécimal de couleur, les fonctions suivantes sont utiles :
rgb: prend en entrée des niveaux de rouge (red), de vert (green), de bleu (blue) et optionnellement d’opacité (alpha), retourne en sortie le code hexadécimal associé;hsv: prend en entrée des niveaux de teinte (hue), de saturation (saturation), de valeur de luminosité (value) et optionnellement d’opacité, retourne en sortie le code hexadécimal associé;hcl: prend en entrée des niveaux de teinte (hue), de chroma (chroma), de luminance (luminance) et optionnellement d’opacité, retourne en sortie le code hexadécimal associé;grayougrey: prend en entrée un niveau de gris entre 0 (noir) et 1 (blanc) et optionnellement d’opacité, retourne en sortie le code hexadécimal associé.
Exemple d’un bleu avec différents niveaux d’opacité :
opacite <- rgb(red = 0, green = 33/255, blue = 78/255, alpha = seq(from = 0, to = 1, by = 0.1))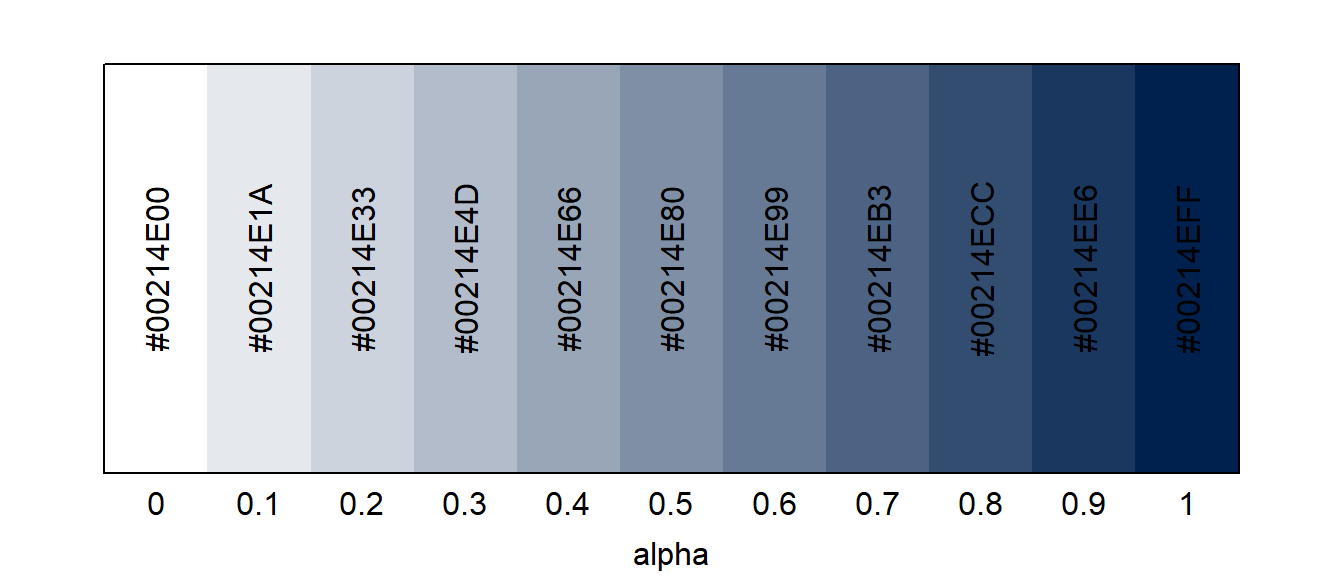
Nombre entier référant à une palette de couleur
Une palette de couleur est définie en R et il est possible de spécifier une couleur par un entier référant à une position dans cette palette. Par défaut, la palette de couleur est la suivante :
palette()## [1] "black" "#DF536B" "#61D04F" "#2297E6" "#28E2E5" "#CD0BBC" "#F5C710" "gray62"Voici un diagramme représentant les couleurs de cette palette selon leur position.
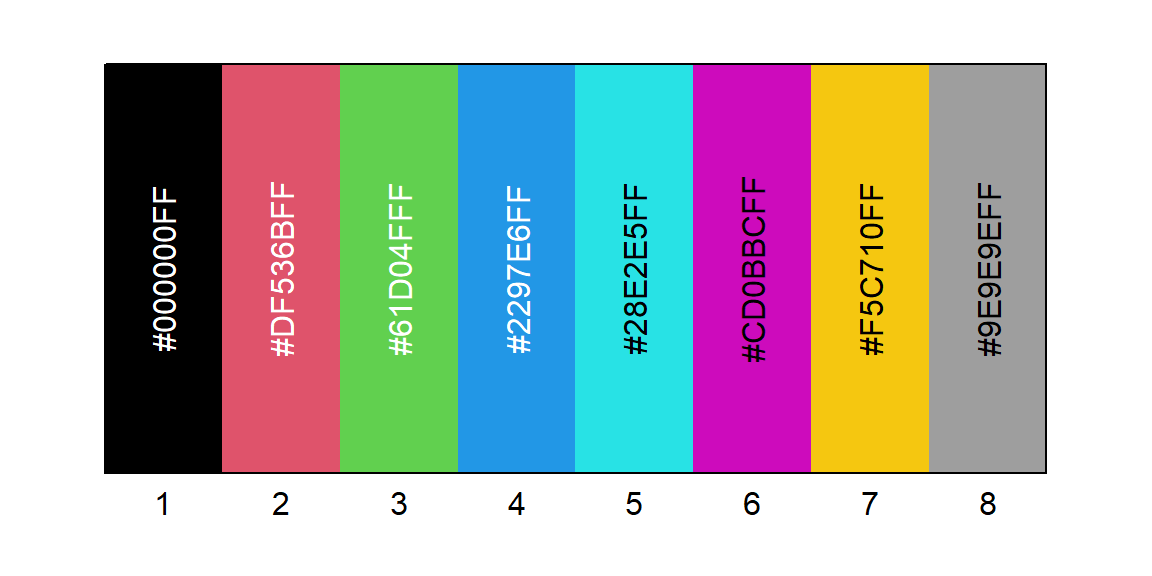
Il est possible de modifier la palette en lui assignant un nouveau vecteur de noms de couleurs ou de chaînes de caractères hexadécimaux de la forme "#rrggbb" ou "#rrggbbaa" pour représenter des couleurs. Certaines fonction R sont pratiques pour créer de tels vecteurs contenant des dégradés de couleurs, particulièrement la fonction hcl.colors. Par exemple, utilisons cette fonction pour modifier la palette de couleurs en un dégradé de 20 couleurs comme suit.
palette(hcl.colors(20))Maintenant, le diagramme représentant les couleurs de la palette selon leur position devient :
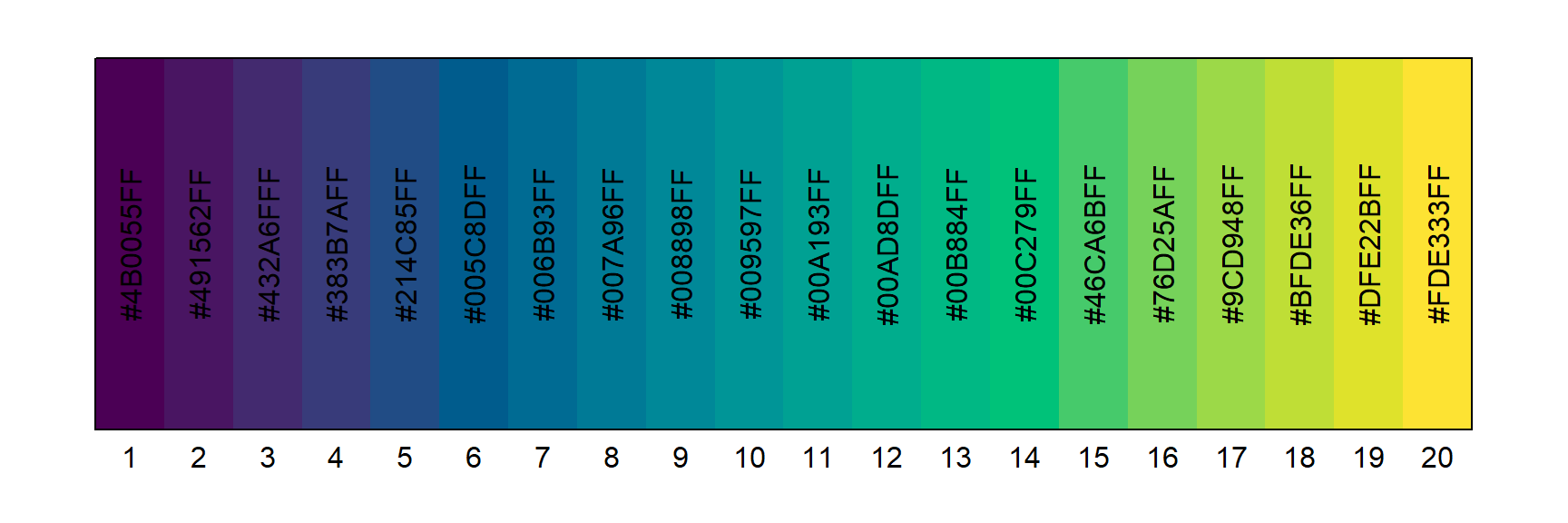
La fonction hcl.colors peut créer des palettes de couleur selon plus d’une centaine de styles, à spécifier via son argument nommé palette. Le style par défaut est "viridis". Il s’agit d’une palette de couleurs popularisée par la librairie graphique Python Matplotlib. Cette palette comporte les avantages de présenter un dégradé uniforme tant en couleur qu’en niveaux de gris (lors d’une impression par exemple) et d’être bien perçu par les daltoniens (du moins pour les formes les plus courantes de daltonisme). Les styles de palette de couleurs acceptés par hcl.colors peuvent être énumérés avec la commande hcl.pals() et visualisés sur la page web suivante : HCL-Based Color Palettes in grDevices.
Pour ramener la palette de couleurs à ses valeurs par défaut, il faut soumettre la commande suivante.
palette("default")Plusieurs packages R permettent de personnaliser les couleurs en R, notamment :
- le package
paletteerqui regroupe un grand nombre de palettes de couleurs supplémentaires offertes par différents packages; - le package
shadesqui offre différentes avenues de manipulation des couleurs (par exemple créer un dégradé entre deux couleurs de notre choix, rendre des couleurs plus foncées ou plus claires, etc.).
2.6 Ajout d’éléments à un graphique
Nous pouvons ajouter des éléments étape par étape à un graphique en R, en appelant les unes après les autres des fonctions graphiques. Le tableau suivant présente les principales fonctions graphiques qui ajoutent des éléments à un graphique initialisé.
| Fonction(s) R | Élément(s) ajouté(s) |
|---|---|
points et matpoints |
points selon des coordonnées |
lines et matlines |
segments de droites reliant des points |
abline |
droites traversant toute la zone graphique |
segments |
segments de droites entre des paires de coordonnées |
arrows |
flèches entre des paires de coordonnées |
rect |
rectangles |
polygon |
polygones quelconques |
legend |
légende |
text |
texte dans la zone graphique |
mtext |
texte dans la marge |
title |
titre |
axis |
axe |
box |
boîte autour de la zone graphique |
qqline |
ligne dans un graphique quantile-quantile théorique |
Aussi, certaines fonctions de création de graphique peuvent devenir des fonctions d’ajout d’éléments à un graphique grâce à l’argument add. C’est la cas notamment des fonctions suivantes : matplot, barplot, hist, boxplot et curve.
En donnant la valeur TRUE à l’argument add lors de l’appel d’une de ces fonctions, elle ajoute des éléments au graphique de la fenêtre graphique active au lieu de créer un nouveau graphique.
Exemple d’ajout de lignes - fonctions abline vs lines
La fonction abline permet d’ajouter à un graphique une droite qui traverse toute la zone graphique.
plot(
stations ~ mag, data = quakes,
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
# Ajustement et ajout d'une droite de régression
lm_out <- lm(stations ~ mag, data = quakes)
abline(lm_out)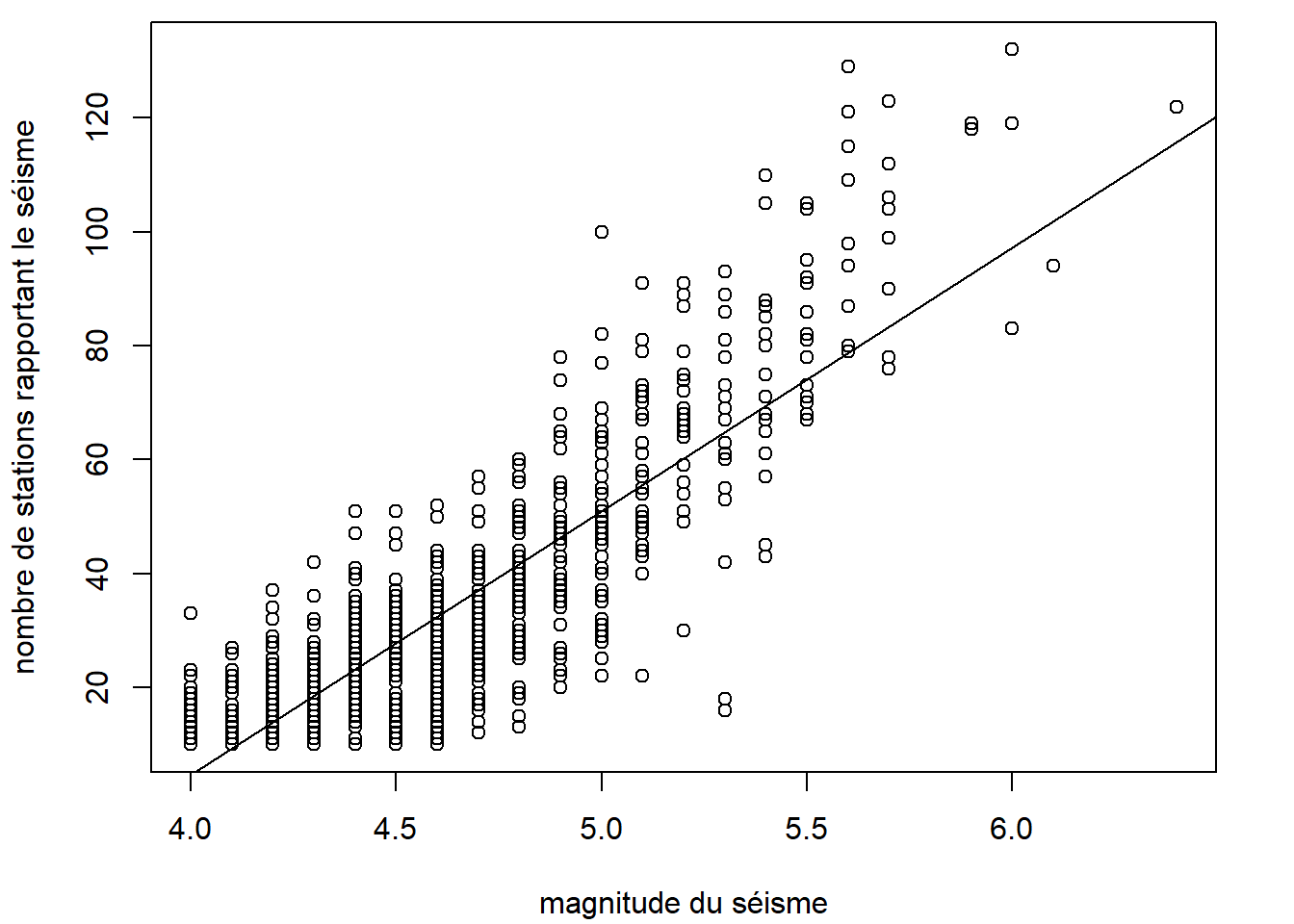
La fonction abline est capable de détecter que l’objet lm_out est une sortie de la fonction lm. Elle trace une droite ayant comme ordonnée à l’origine le premier coefficients du modèles ajusté et comme pente le deuxième coefficient. Nous aurions pu spécifier manuellement l’ordonnée à l’origine et la pente de la droite avec les arguments a et b, ou encore tracer une ligne horizontale avec l’argument h ou verticale avec l’argument v.
Avec la fonction lines, nous pouvons ajouter des segments de droites reliant des points pour lesquels les coordonnées sont fournies.
# Calcul des médianes de stations par modalité de mag_catego
out_agg <- aggregate(stations ~ mag_catego, data = quakes, FUN = median)
out_agg$mag_catego <- as.numeric(out_agg$mag_catego)
boxplot(
stations ~ mag_catego, data = quakes,
xlab = "modalité de magnitude",
ylab = "nombre de stations"
)
lines(x = out_agg, lty = 6, lwd = 2, col = 4)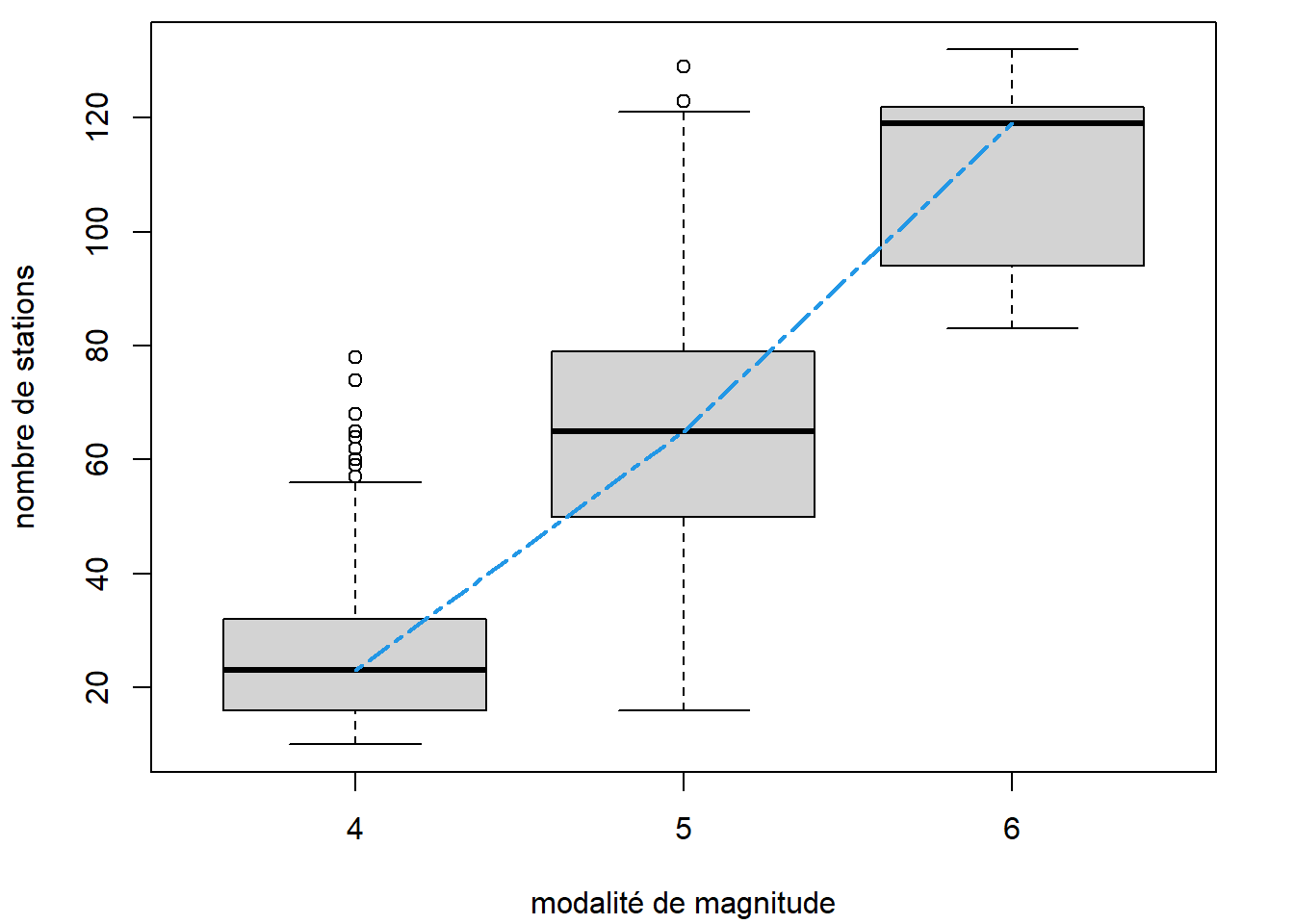
Exemple d’ajout d’une légende - fonction legend
Nous avions mentionné précédemment que le graphique que nous avons produit avec la fonction matplot devrait contenir une légende. Ajoutons-lui en une maintenant.
matplot(
x = quakes_large[, c("mag_Est", "mag_Ouest")],
y = quakes_large[, c("stations_Est", "stations_Ouest")],
pch = 2:1, col = c("blue", "green"),
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
legend(
x = "topleft",
legend = c("Est", "Ouest"),
pch = 2:1, col = c("blue", "green"),
title = "région"
)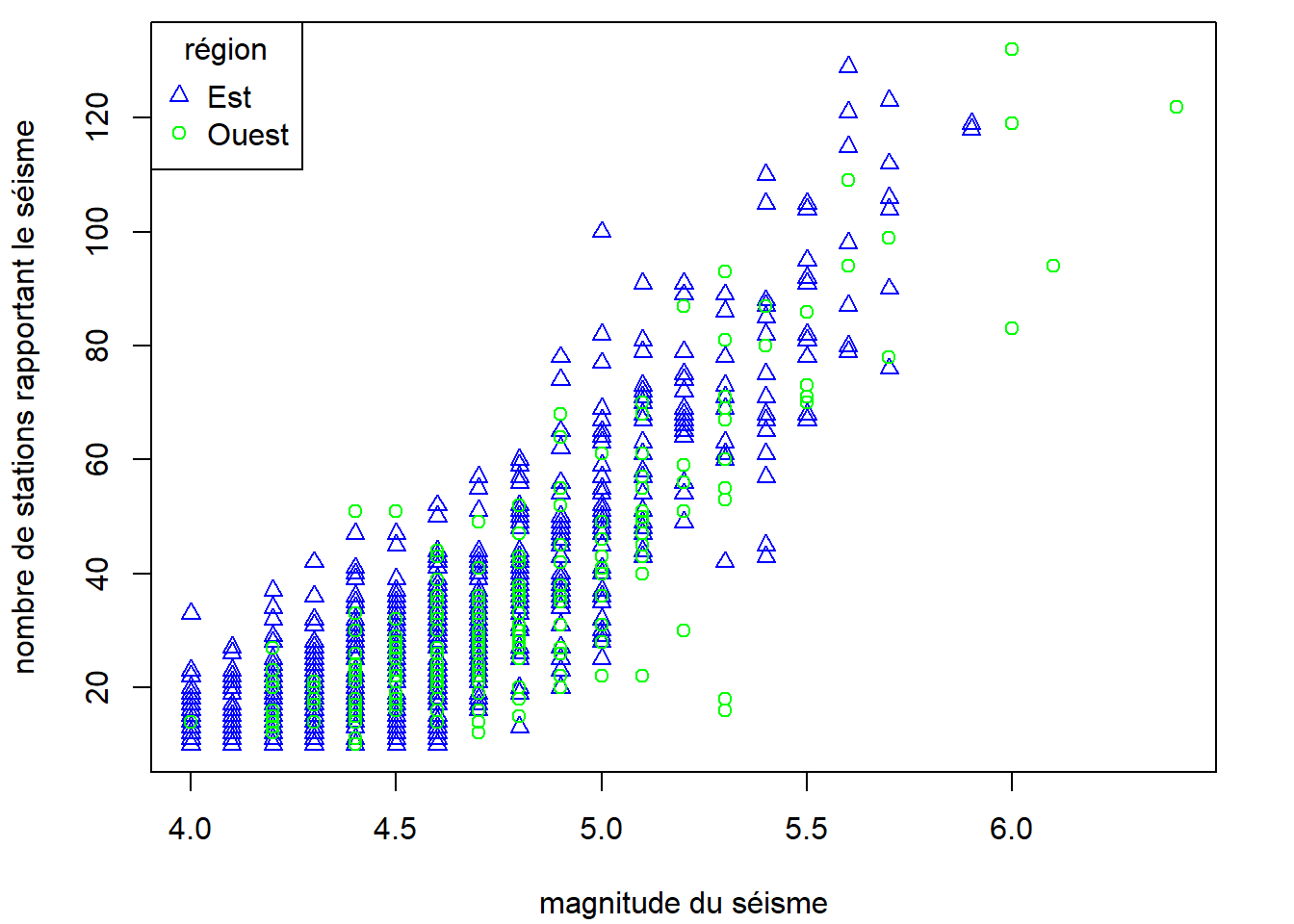
La localisation de la légende peut être spécifiée comme ici par un mot clé fourni à l’argument x ("bottomright", "bottom", "bottomleft", "left", "topleft", "top", "topright", "right" ou "center"), ou par des coordonnées exactes (arguments x et y).
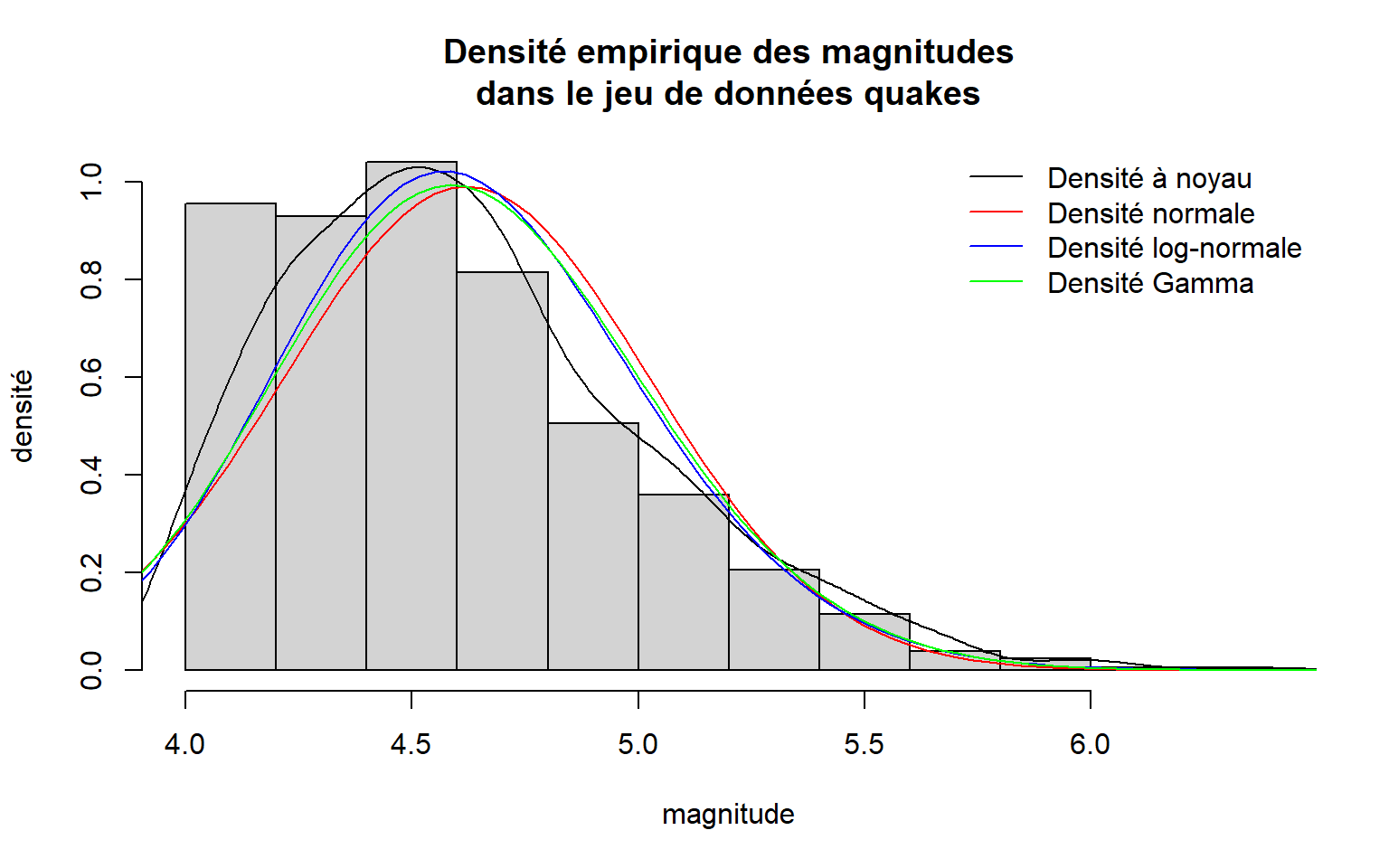
Exemple d’ajout de courbes à un histogramme et d’une légende
Voici un exemple plus élaboré, dans lequel nous exploitons notamment l’argument add de la fonction curve pour ajouter des éléments à un graphique.
# Initialisation de l'histogramme
hist(
x = quakes$mag, freq = FALSE,
main = "Densité empirique des magnitudes\ndans le jeu de données quakes",
xlab = "magnitude", ylab = "densité"
)
# Ajout de la courbe de densité à noyau
lines(density(quakes$mag), xlim = range(quakes$mag))
# Ajout de courbes de densité théoriques avec paramètres estimés à partir des données
moy <- mean(quakes$mag)
et <- sd(quakes$mag)
curve(
dnorm(x, mean = moy, sd = et),
add = TRUE, col = "red", xlim = c(3.5, 7)
)
curve(
dlnorm(x, meanlog = mean(log(quakes$mag)), sdlog = sd(log(quakes$mag))),
add = TRUE, col = "blue", xlim = c(3.5, 7)
)
curve(
dgamma(x, shape = moy^2/et^2, rate = moy/et^2),
add = TRUE, col = "green", xlim = c(3.5, 7)
)
# Ajout d'une légende
legend(
x = "topright", bty = "n",
col = c("black", "red", "blue", "green"), lty = 1,
legend = c("Densité à noyau", "Densité normale", "Densité log-normale", "Densité Gamma")
)
Astuce :
Il est possible d’insérer des sauts de ligne dans un élément textuel. Ceux-ci sont représentés par la chaîne de caractères "\n". Cette astuce a été utilisée dans le graphique précédent pour obtenir un titre s’étalant sur deux lignes.
2.7 Possibilités graphiques spécifiques
2.7.1 Annotations mathématiques
Des annotations mathématiques sont des caractères spéciaux communs en science, telle que des exposants, des indices, des fractions, des lettres grecques, etc. Tout élément textuel d’un graphique peut en contenir (p. ex. les valeurs données à un argument main, xlab, ylab, labels, legend, text, etc.). La fiche d’aide intitulée plotmat énumère toutes les annotations possibles. Ces annotations impliquent une syntaxe particulière, qui ressemble un peu à du LaTeX. Elles doivent être exprimée sous la forme d’une expression R. La fonction expression permet de créer une telle expression.
Exemple d’appel à la fonction expression
Pour qu’un élément textuel puisse contenir une annotation mathématique, il doit être créé par un appel à la fonction expression, comme c’est le cas pour les valeurs fournies aux arguments xlab, ylab et labels dans la commande de création de graphique suivante.
curve(
expr = sin, from = -4, to = 4,
main = "Fonction sinus",
xlab = expression(theta),
ylab = expression(sin~(theta)),
xaxt = "n" # pour omettre la création automatique de l'axe des x
)
axis( # pour créer manuellement l'axe des x
side = 1,
at = c(-pi, -pi/2, 0, pi/2, pi),
labels = expression(-pi, -pi/2, 0, pi/2, pi)
)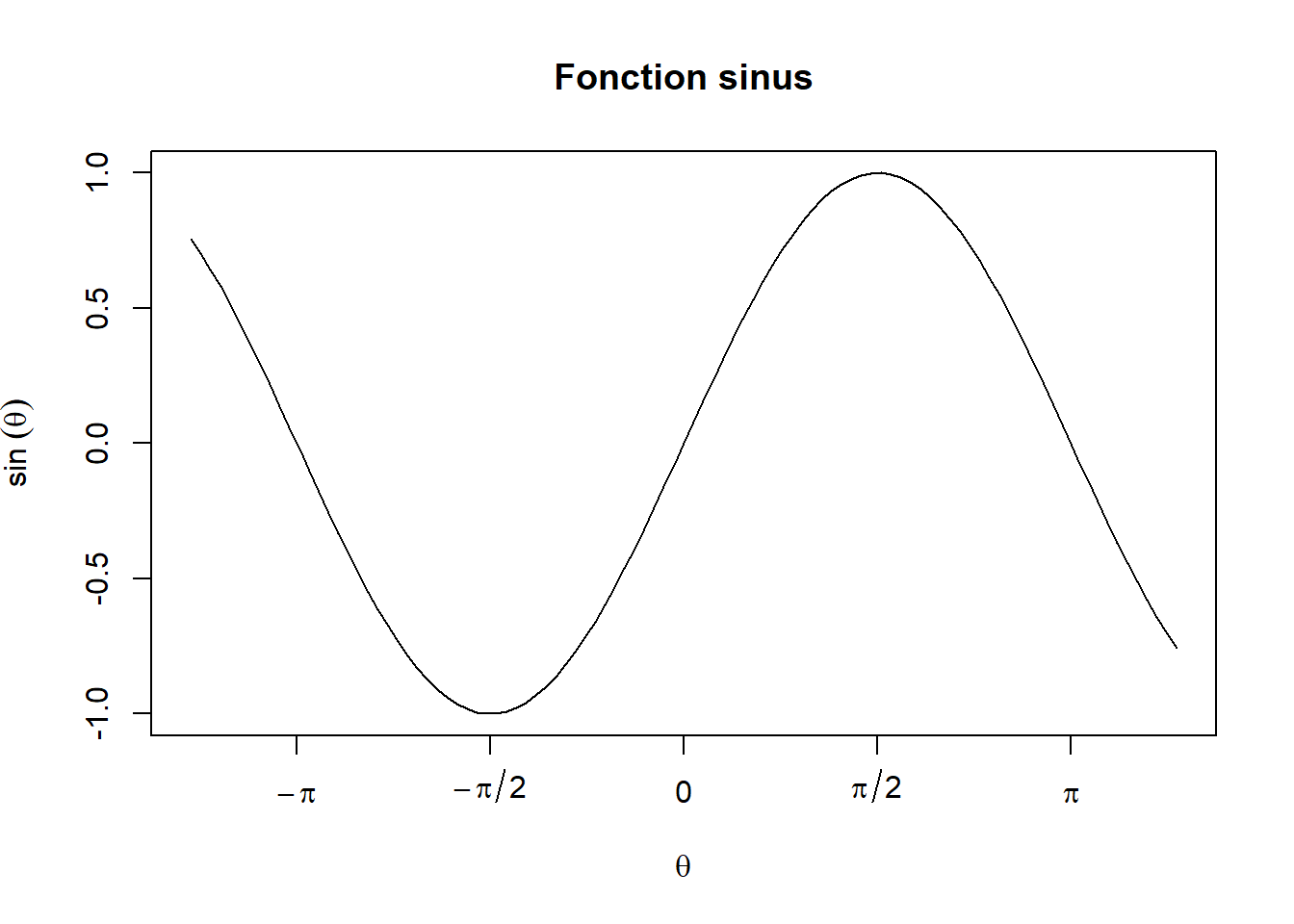
Les valeurs theta et pi ont été remplacées par leurs lettres grecques correspondantes (θ et π) dans le graphique. Le symbole ~ est quant à lui devenu un espace.
Remarquons qu’en fournissant plusieurs arguments à la fonction expression lors de la spécification des valeurs de labels, nous avons créé un vecteur d’éléments textuels comprenant des annotations mathématiques.
Exemple d’appel à la fonction paste dans une expression
Reprenons le graphique représentant une fonction polynomiale de degré deux que nous avons créé précédemment avec la fonction curve. Modifions le nom de l’axe des y de façon à y faire apparaître l’exposant 2 réellement en exposant.
curve(
expr = x^2 + 5*x - 25,
from = -23, to = 18, n = 200,
main = "Fonction polynomiale de degré deux",
ylab = expression(paste(x^2, "+ 5x - 25"))
)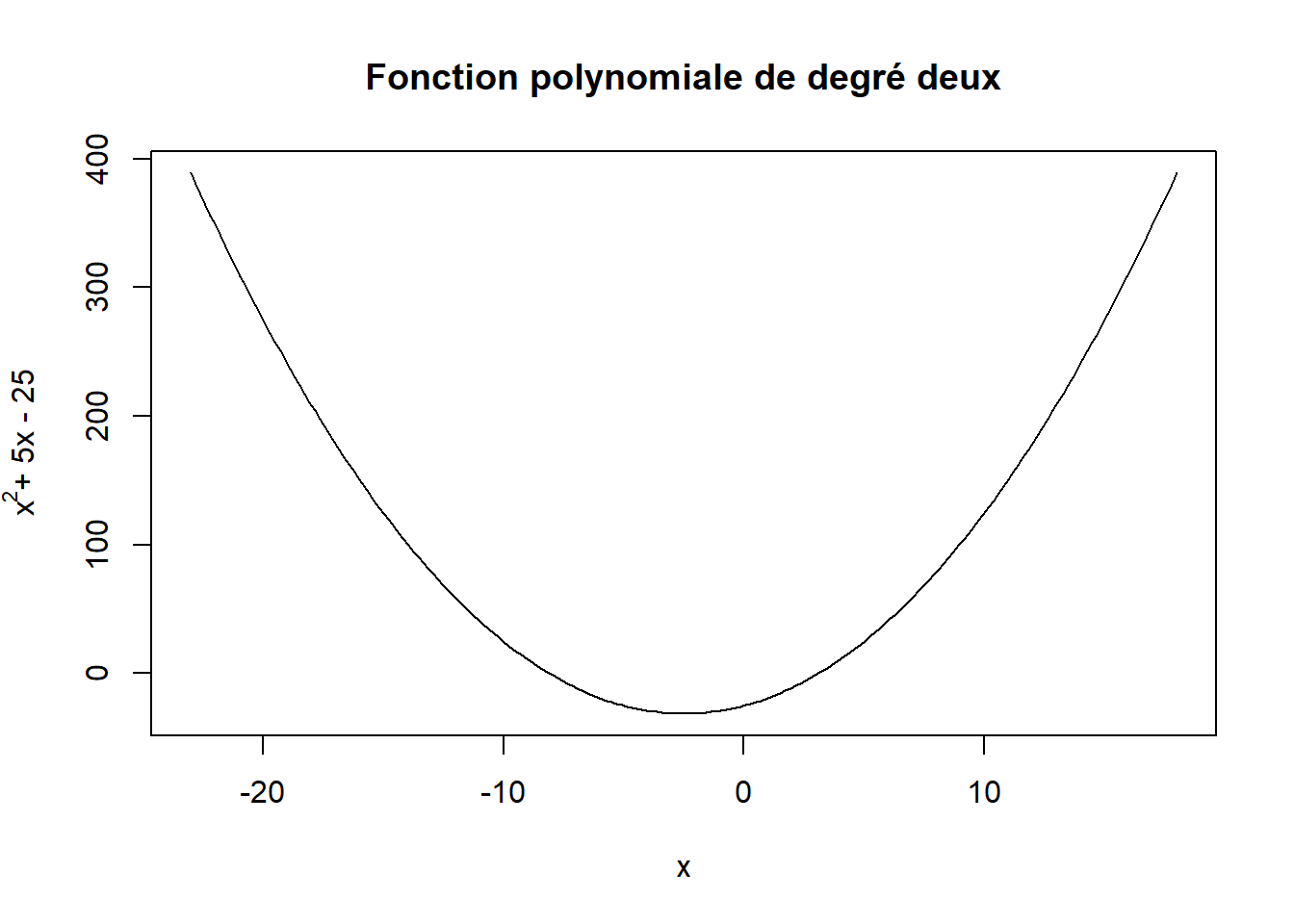
Si un élément textuel doit être formé de parties à interpréter sous forme d’expressions mathématiques et d’autres sous forme de chaînes de caractères ordinaires, il faut assembler ces parties avec la fonction paste, comme dans l’exemple précédent. Notons que la fonction paste n’agit pas ici tout à fait comme d’habitude. Dans des expressions mathématiques, paste ne travaille pas de façon vectorielle et ne possède pas d’arguments. La fonction ne fait que juxtaposer des parties d’éléments textuels.
Exemple d’annotations mathématiques plus poussées
Dans le graphique intitulé « Densité empirique des magnitudes dans le jeu de données quakes », introduisons des notations mathématiques dans la légende.
# Initialisation de l'histogramme
hist(
x = quakes$mag, freq = FALSE,
main = "Densité empirique des magnitudes\ndans le jeu de données quakes",
xlab = "magnitude", ylab = "densité"
)
# Ajout de la courbe de densité à noyau
lines(density(quakes$mag), xlim = range(quakes$mag))
# Ajout de courbes de densité théoriques avec paramètres estimés à partir des données
moy <- mean(quakes$mag)
et <- sd(quakes$mag)
curve(
dnorm(x, mean = moy, sd = et),
add = TRUE, col = "red", xlim = c(3.5, 7)
)
curve(
dlnorm(x, meanlog = mean(log(quakes$mag)), sdlog = sd(log(quakes$mag))),
add = TRUE, col = "blue", xlim = c(3.5, 7)
)
curve(
dgamma(x, shape = moy^2/et^2, rate = moy/et^2),
add = TRUE, col = "green", xlim = c(3.5, 7)
)
# Ajout d'une légende
legend(
x = "topright", bty = "n",
col = c("black", "red", "blue", "green"), lty = 1,
legend = c(
"Densité à noyau",
expression(
paste(
"N",
bgroup("(",list(mu == bar(x), sigma^2 == s[x]^2),")")
)
),
expression(
paste(
"Log-N",
bgroup("(",list(mu == bar(y), sigma^2 == s[y]^2),")"),
" avec ",
y == ln(x)
)
),
expression(
paste(
"Gamma",
bgroup("(",list(alpha == bar(x)^2/s[x]^2, beta == bar(x)/s[x]^2),")")
)
)
)
)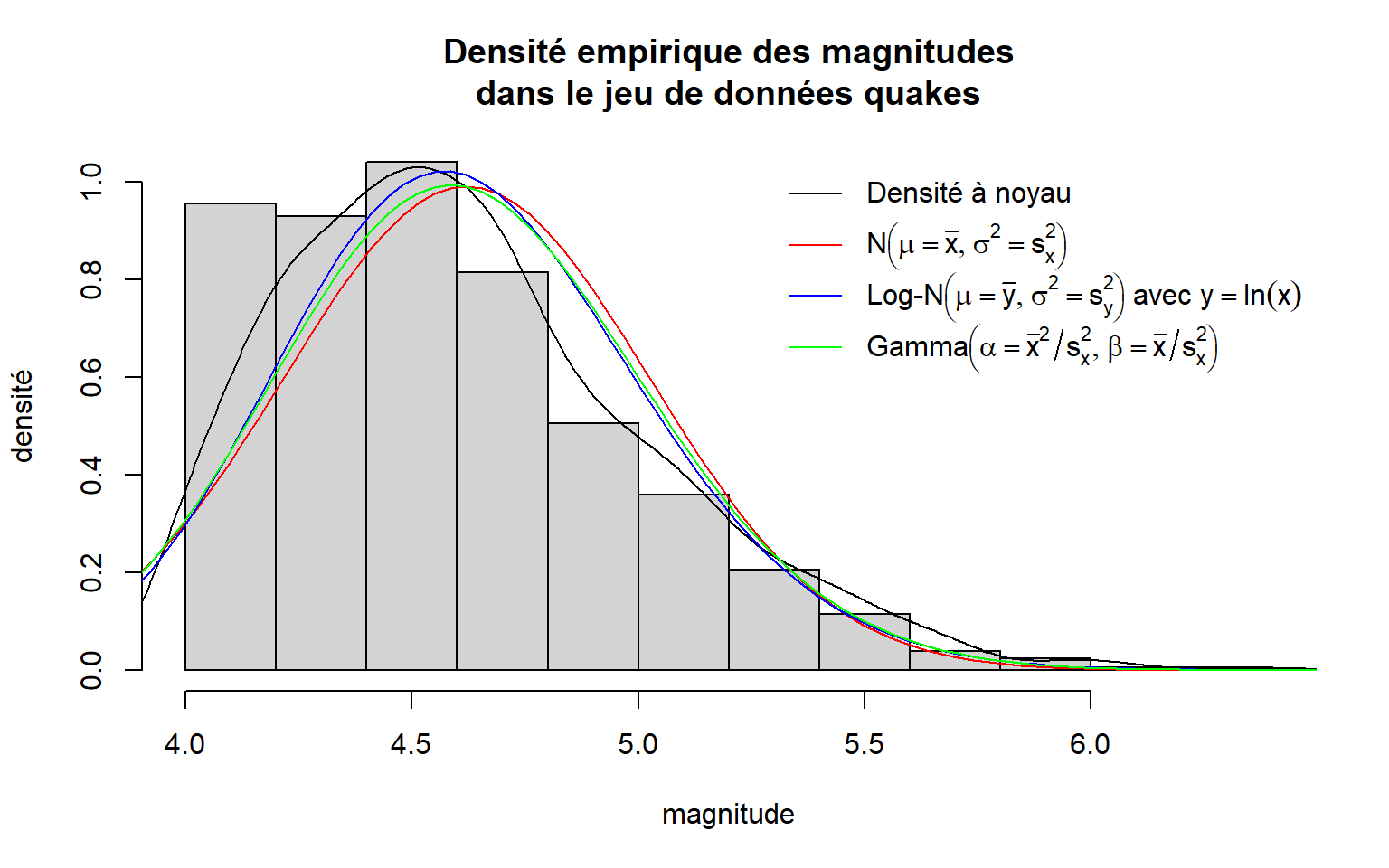
Dans ce code, les trois derniers éléments du vecteur fourni à l’argument legend de la fonction du même nom sont des expressions. Ces éléments sont créés par des appels à la fonction expression. Penchons-nous sur un de ces appels pour tenter de mieux le comprendre.
expression(
paste(
"Log-N",
bgroup("(",list(mu == bar(y), sigma^2 == s[y]^2),")"),
" avec ",
y == ln(x)
)
)L’appel à la fonction expression contient un appel à la fonction paste. Comme expliqué à l’exemple précédent, nous sommes contraints à cette syntaxe parce que le libellé doit contenir à la fois des chaînes de caractères ordinaires (ici "Log-N" et " avec ") et des expressions mathématiques. La première expression mathématique dans le paste précédent est bgroup("(",list(mu == bar(y), sigma^2 == s[y]^2),")"). Cette expression permet de créer l’annotation ressemblant à (μ=ˉy,σ2=s2y) grâce aux interprétations suivantes de ses éléments:
bgroup("(", x, ")")permet d’encadrer des éléments de parenthèses dont la hauteur s’adapte à la hauteur des éléments,list(x, y)sépare des éléments par une virgule (pas la même signification que la fonctionlistrégulière),mudevient la lettre grecque μ,==devient un signe d’égalité,bar(y)devient ˉy,sigmadevient la lettre grecque σ,^2devient un exposant,[y]devient un indice,- etc.
Autres options :
Le package latex2exp permet d’utiliser dans un code R de création de graphique des équations LaTeX, au lieu d’expressions R, pour ajouter des annotations mathématiques dans un graphique.
Le package tikzDevice permet quant à lui non seulement d’utiliser des équations LaTeX dans le code R, mais aussi d’obtenir, dans un graphique R, des annotations mathématiques utilisant la même police de caractère que LaTeX. Les graphiques produits en exploitant ce package peuvent donc s’harmoniser parfaitement à un document rédigé en LaTeX.
Exemple d’annotations mathématiques comprenant une valeur tirée d’un objet R
Il est même possible d’utiliser une valeur tirée d’un objet R dans des annotations mathématiques. Pour ce faire, il faut faire appel à la fonction substitute au lieu de la fonction expression pour créer l’expression mathématique.
Voici un exemple, qui reprend l’exemple dans lequel une droite de régression a été ajoutée à un diagramme de dispersion.
plot(
stations ~ mag, data = quakes,
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
# Ajustement et ajout d'une droite de régression
lm_out <- lm(stations ~ mag, data = quakes)
abline(lm_out)
# Ajout de la valeur du R carré ajusté
lm_out_R2 <- round(summary(lm_out)$r.squared, 3)
text(
x = 6, y = 15,
label = substitute(
exp = paste(R^2, " = ", valeur_R2),
env = list(valeur_R2 = lm_out_R2)
)
)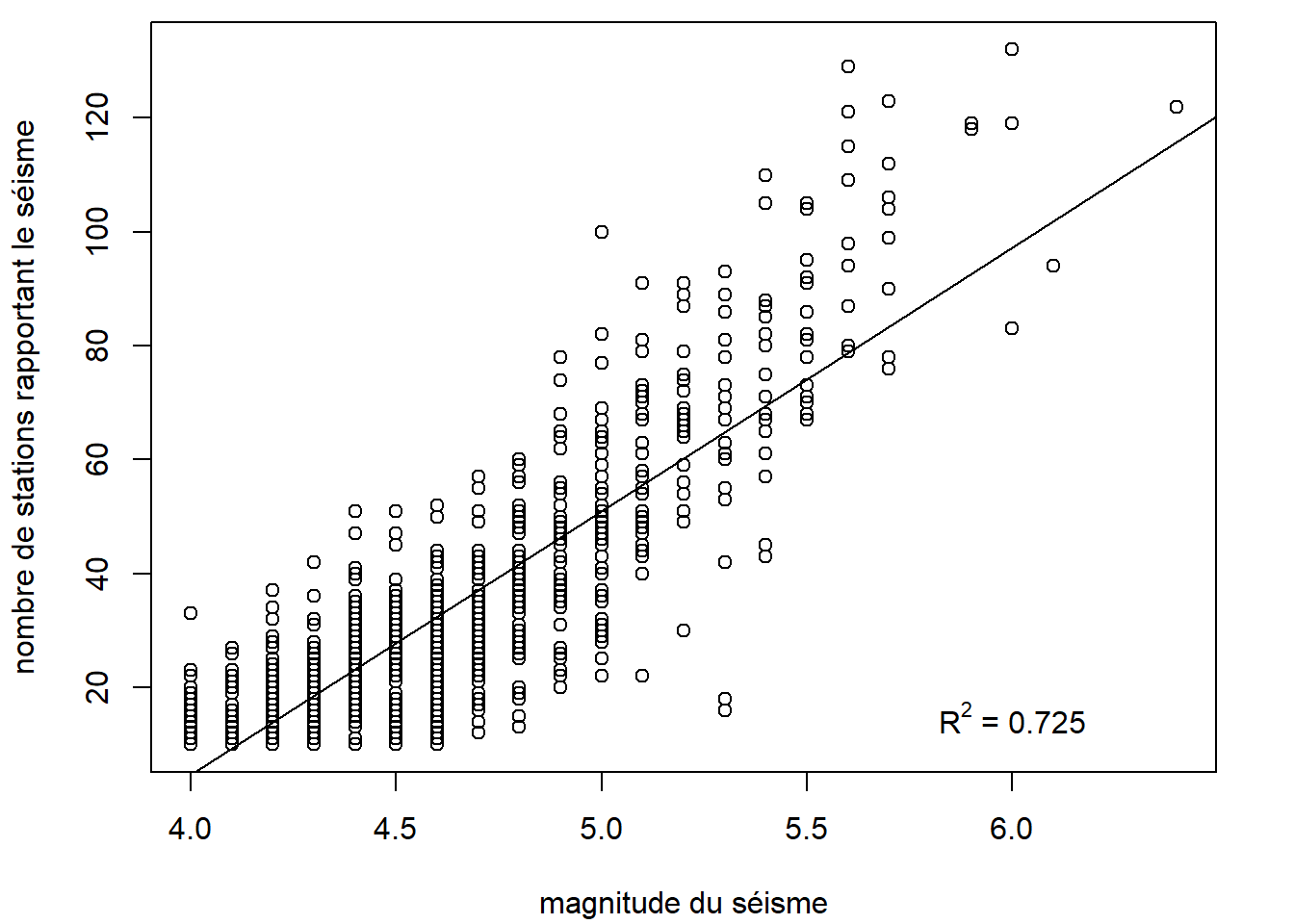
Dans ce graphique, nous avons ajouté une annotation textuelle mentionnant la valeur du R2 ajusté de la régression. Avec substitute, nous avons créé une expression R dans laquelle un élément a été évalué avant de créer l’expression. Cette évaluation s’est effectuée à partir d’un environnement spécifié dans le deuxième argument.
Mentionnons que la fonction bquote aurait aussi pu être utilisée en remplacement de substitute comme suit.
text(
x = 6, y = 15,
label = bquote(R^2 == .(lm_out_R2))
)Les possibilités d’annotations mathématiques sont grandes, mais un peu compliquées à comprendre, car elles font intervenir de la métaprogrammation (des notes sont consacrées à ce sujet).
2.7.2 Plusieurs graphiques dans une même fenêtre
Il est possible de diviser la fenêtre graphique en sous-fenêtres. Les deux principaux outils offerts dans le système de base pour effectuer cette division sont les suivants :
- arguments
mfrowoumfcolde la fonctionpar: produit une grille de sous-fenêtres de tailles égales; - fonction
layout: permet de contrôler les dimensions des sous-fenêtres.
Exemple : Sous-fenêtres de tailles égales - argument mfrow ou mfcol de par
Réunissons quatre représentations de la variable mag du jeu de données quakes dans un seul graphique.
# Modification du paramètre graphique mfrow de façon à diviser la
# fenêtre graphique en 4 sous-fenêtres sur une grille 2 par 2
par_default <- par(mfrow = c(2, 2))
# Graphique dans la première sous-fenêtre
hist(
x = quakes$mag, freq = FALSE,
main = "", xlab = "magnitude", ylab = "densité",
)
# Graphique dans la deuxième sous-fenêtre
plot(
x = density(quakes$mag),
main = "", xlab = "magnitude", ylab = "densité"
)
# Graphique dans la troisième sous-fenêtre
boxplot(x = quakes$mag, horizontal = TRUE, xlab = "magnitude")
# Graphique dans la quatrième sous-fenêtre
qqnorm(
y = quakes$mag,
main = "", xlab = "quantiles théoriques normaux", ylab = "quantiles empiriques"
)
qqline(quakes$mag)
# Réattribution des valeurs par défaut aux paramètres graphiques
par(par_default)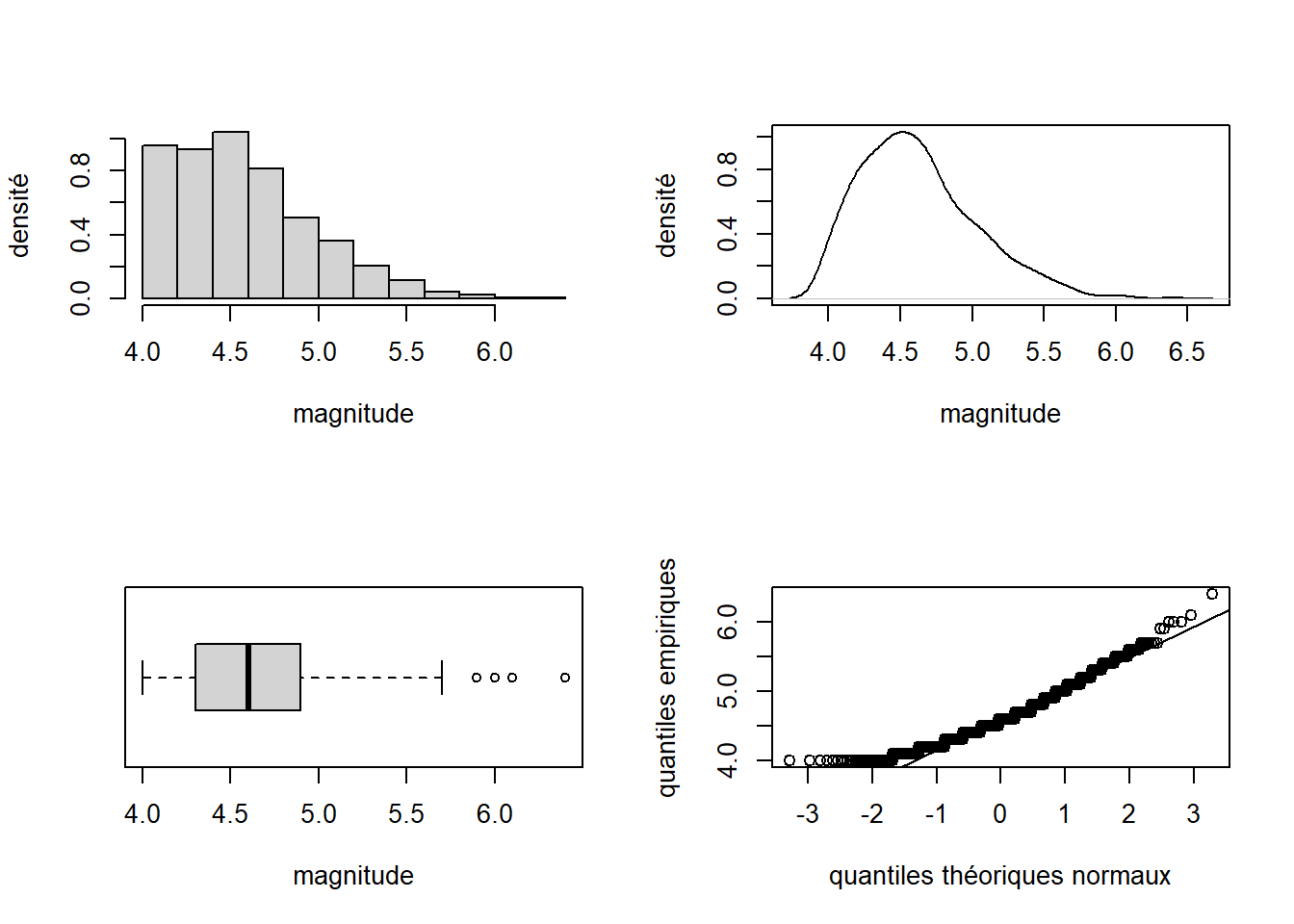
L’argument mfrow = c(2, 2) a provoqué la division de la fenêtre graphique en une grille de sous-fenêtres comprenant 2 lignes et 2 colonnes. Les quatre graphiques produits après avoir modifié cet argument ont été distribués, ligne par ligne, dans cette grille. Si l’argument mfcol avait été utilisé au lieu de mfrow, les graphiques auraient été distribués en remplissant la grille une colonne à la fois, de la première à la dernière. Afin de retrouver une fenêtre graphique non divisée en sous-fenêtre, il ne faut pas oublier de remettre à c(1, 1) la valeur du paramètre graphique mfrow ou mfcol (ce qui est fait ci-dessus par la commande par(par_default)).
Exemple : Sous-fenêtres de tailles inégales - fonction layout
La fonction layout découpe aussi la fenêtre graphique en grille de sous-fenêtres. Cependant, les hauteurs et largeurs des bandes du quadrillage peuvent être personnalisées à l’aide d’arguments de la fonction (widths et heights). Le premier argument à fournir à la fonction layout, nommé mat, est une matrice de même dimension que la grille à créer. Cette matrice peut uniquement contenir des nombres entiers entre 0 et le nombre total de sous-graphiques à insérer dans la fenêtre, inclusivement. Dans les commandes qui suivent l’appel à la fonction layout, le premier graphique produit est affiché dans la sous-fenêtre associée au chiffre 1, le deuxième dans la sous-fenêtre associée au chiffre 2 et ainsi de suite. L’attribution du chiffre zéro à une sous-fenêtre signifie qu’aucun graphique ne doit être affiché dans cette sous-fenêtre. L’attribution d’un même entier positif à plusieurs sous-fenêtres adjacentes permet de les fusionner en une seule sous-fenêtre.
La fonction layout.show permet de visualiser les sous-fenêtres créées.
Voici un exemple de découpage en sous-fenêtre avec layout.
layout(matrix(c(1, 2, 3, 3), nrow = 2), widths = c(3, 2))
layout.show(n = 3)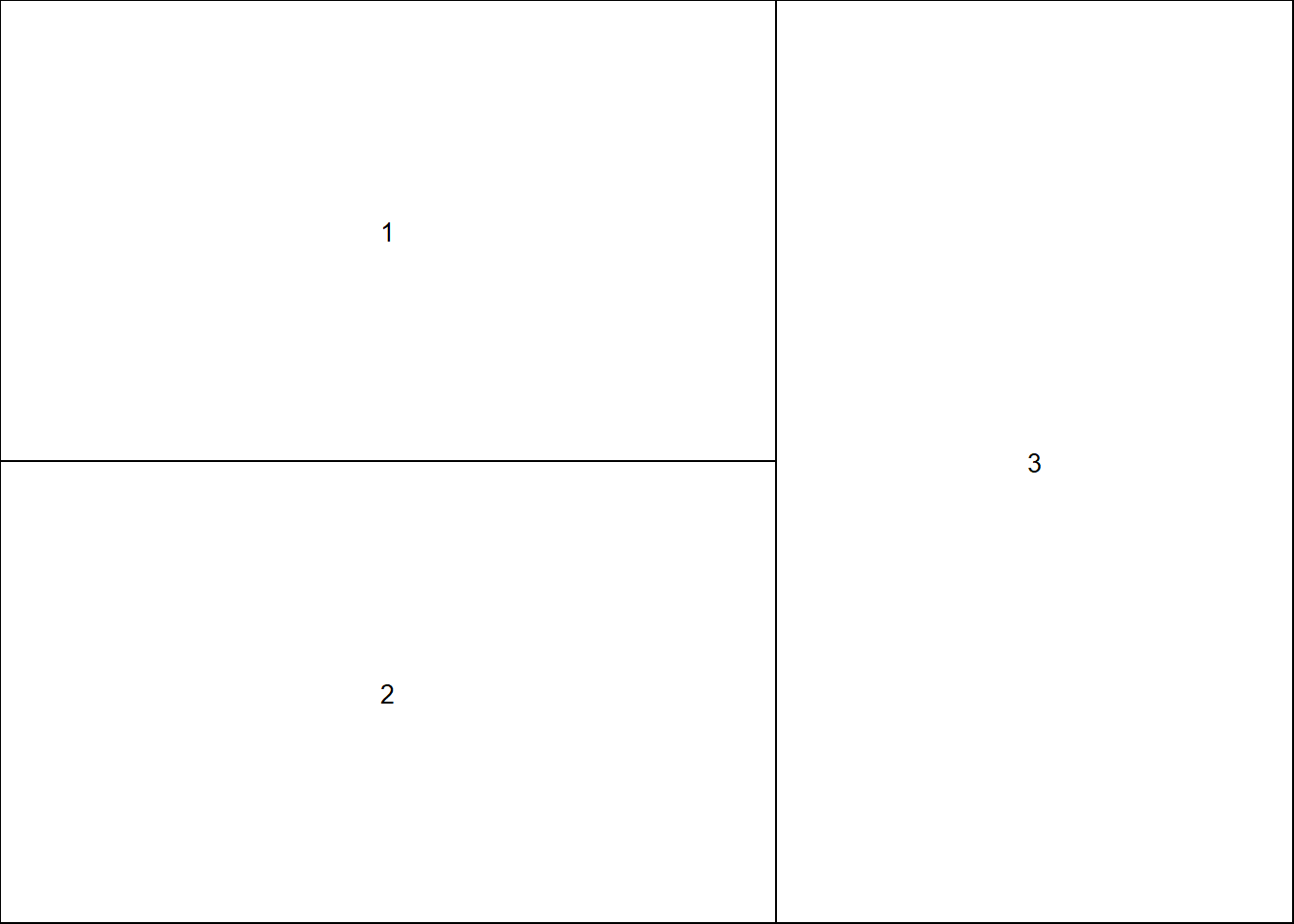
Maintenant, répartissons des graphiques concernant les données quakes dans les sous-fenêtres de la disposition que nous venons de créer avec layout.
# Configuration des sous-fenêtres
layout(matrix(c(1, 2, 3, 3), nrow = 2), widths = c(3, 2))
# Graphique dans la première sous-fenêtre
hist(
x = quakes$mag, freq = FALSE,
main = "", xlab = "magnitude", ylab = "densité",
)
# Graphique dans la deuxième sous-fenêtre
boxplot(x = quakes$mag, horizontal = TRUE, xlab = "magnitude")
# Graphique dans la troisième sous-fenêtre
qqnorm(
y = quakes$mag,
main = "", xlab = "quantiles théoriques normaux", ylab = "quantiles empiriques"
)
qqline(quakes$mag)
# Réattribution de la valeur par défaut de layout
layout(matrix(1))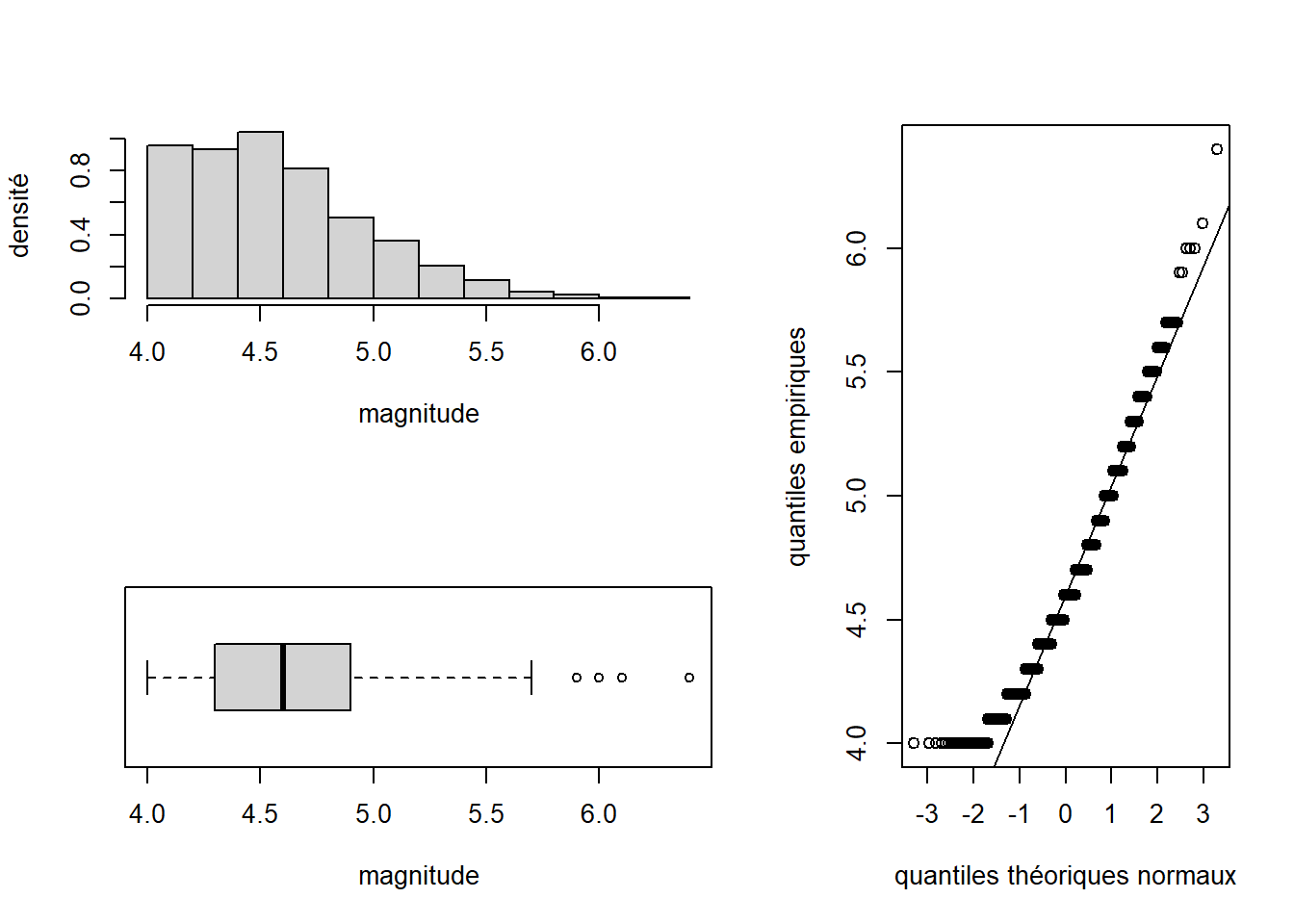
Comme pour les paramètres modifiés avec la fonction par, le découpage effectué par layout est effectif tant qu’il n’est pas modifié de nouveau avec layout ou jusqu’à la fin de la session R. Une bonne pratique est donc de redonner à layout sa valeur par défaut à la fin du code de création du graphique avec l’instruction layout(matrix(1)), comme nous l’avons fait ci-dessus.
Nous pourrions améliorer ce graphique en ajustant les marges. Nous pourrions également mettre des sous-titres et un titre global.
# Enregistrement des valeurs par défaut aux paramètres graphiques
all_par_default <- par(no.readonly = TRUE)
# Configuration des sous-fenêtres
layout(matrix(c(1, 2, 3, 3), nrow = 2), widths = c(3, 2))
# Pour créer un espace pour le titre global (dans la marge externe)
par(oma = c(0, 0, 3, 0))
# Graphique dans la première sous-fenêtre
par(mar = c(3.1, 4.1, 2.1, 2.1), cex.main = 1)
hist(x = quakes$mag, freq = FALSE, main = "Histogramme", ylab = "densité")
# Graphique dans la deuxième sous-fenêtre
par(mar = c(5.1, 4.1, 2.1, 2.1))
boxplot(
x = quakes$mag, horizontal = TRUE,
main = "Diagramme en boîte", xlab = "magnitude"
)
# Graphique dans la troisième sous-fenêtre
qqnorm(
y = quakes$mag,
main = "Diagramme quantile-quantile",
xlab = "quantiles théoriques normaux",
ylab = "quantiles empiriques de la magnitude"
)
qqline(quakes$mag)
# Ajout du titre global dans la marge externe
mtext(
text = "Densité empirique des magnitudes dans le jeu de données quakes",
outer = TRUE, cex = 1.2, line = 1.5
)
# Réattribution des valeurs par défaut aux paramètres graphiques
par(all_par_default)
layout(matrix(1))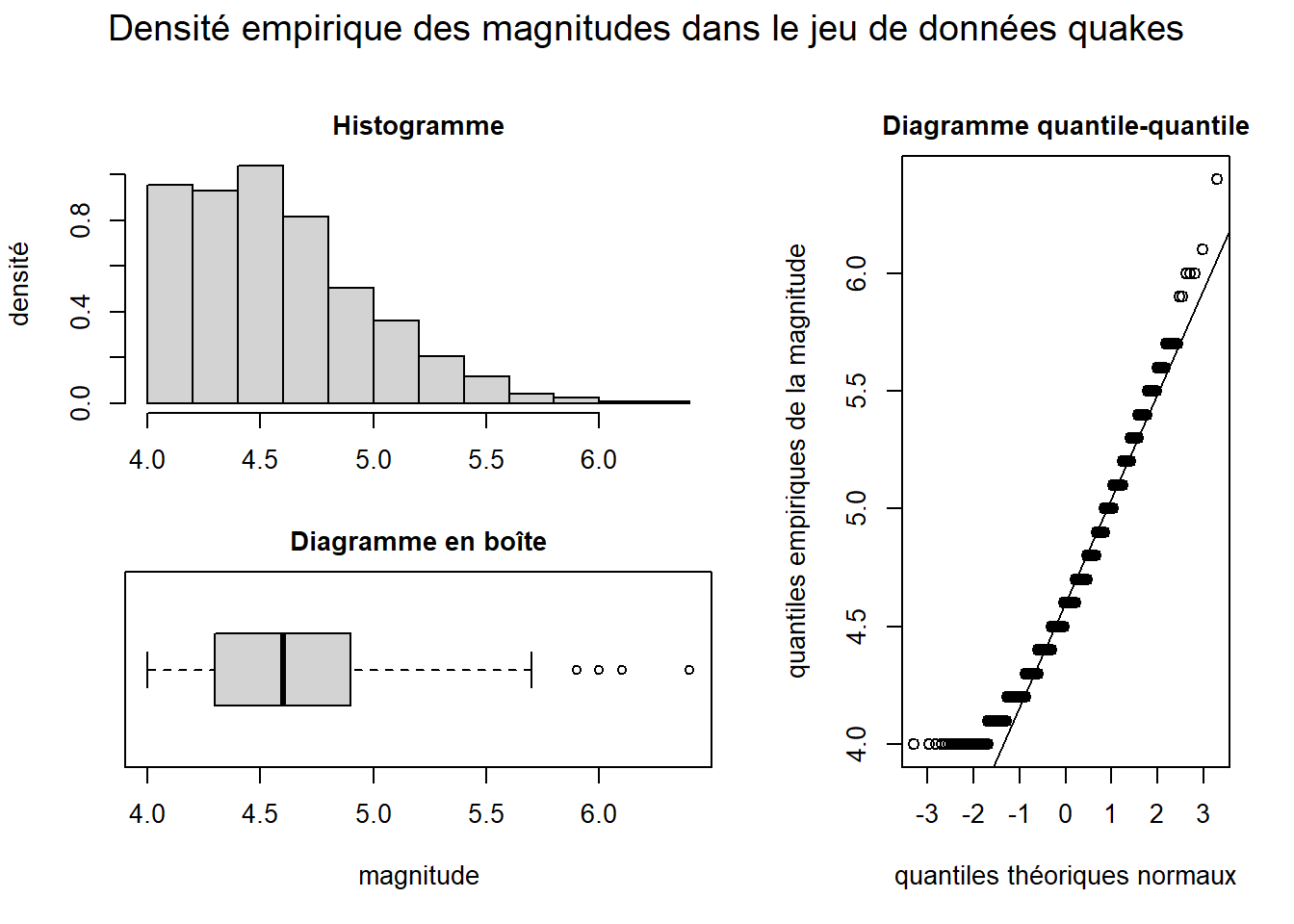
Autres exemples d’utilisation de layout :
2.8 Aspects techniques
Créer un graphique en R signifie soumettre un programme R qui génère le graphique. Pour produire de nouveau le même graphique, il suffit de conserver le programme permettant de générer le graphique et de le soumettre de nouveau dans la console. Le fait de produire le graphique par un programme plutôt que par un menu dans lequel nous sélectionnons des options permet d’automatiser le travail et de sauver du temps lorsque nous avons à produire plusieurs graphiques similaires.
2.8.1 Fenêtres graphiques
En R, les graphiques sont par défaut tous créés dans la même fenêtre. RStudio conserve un historique des graphiques, ce qui permet de réafficher un graphique produit antérieurement, mais au cours d’une même session R.
Nous pouvons aussi choisir d’ouvrir une nouvelle fenêtre graphique avec la commande dev.new() ou avec
windows()sur Windows,quartz()sur macOS,X11()sur Linux.
Les dimensions de la fenêtre graphique courante sont les suivantes
par("din")# ou
dev.size()## [1] 7 5Ce paramètre graphique n’est pas modifiable (R.O. = Read Only dans la documentation de la fonction par). Cependant, les dimensions d’une nouvelle fenêtre ouverte avec windows, quartz ou X11 peuvent être spécifiée avec les arguments width et height. Exemple :
windows(width = 10, height = 7.5)Commandes utiles :
dev.list(): pour voir la liste de toutes les fenêtres graphiques ouvertes,dev.cur(): pour connaître la fenêtre graphique courante,dev.off(): pour fermer la fenêtre graphique courante (peut aussi être fermée avec la souris).
Pour d’informations sont offertes dans la fiche d’aide R nommée dev.
2.8.2 Enregistrement d’un graphique
En RStudio, nous pouvons enregistrer un graphique dans l’onglet « Plots » par le menu Export. Nous pouvons aussi le faire, comme dans l’exemple suivant, avec les fonctions bmp, postscript, pdf, png, tiff, svg ou jpeg, selon le format désiré.
# Ouverture de la connexion avec un fichier
png("test.png")
# Code pour créer le graphique
plot(x = quakes$mag, y = quakes$stations)
# potentiellement plusieurs lignes de code ici
# Fermeture de la connexion avec le fichier
dev.off()En fait, ces fonctions redirigent l’affichage de graphiques vers un fichier. L’instruction dev.off() est nécessaire pour mettre un terme à la communication entre R et le fichier ouvert.
2.8.3 Astuces diverses
À titre de référence, voici une liste de quelques autres fonctions techniques utiles avec des graphiques produits à l’aide du système de base en R.
locator: pour identifier avec la souris une position;identify: pour identifier avec la souris des observations;clip: pour restreindre la zone d’ajouts dans un graphique;jitter: pour ajouter un peu de bruits à des valeurs numériques, ce qui peut permettre de visualiser plus facilement des observations superposées.
Aussi, il est bon de savoir que plusieurs fonctions graphiques de base peuvent, tout comme hist, retourner des valeurs en plus de créer un graphique. Les valeurs retournées contiennent, par exemple :
- les coordonnées de certains éléments dans le graphique, par exemple :
- dans un histogramme produit avec
hist: les coordonnées des limites et des centres des barres (en d’autres mots des intervalles), - dans un diagramme à barres produit avec
barplot: les coordonnées centrales des barres sur l’axe de la variable catégorique; - etc.;
- dans un histogramme produit avec
- des statistiques calculées pour produire le graphique, par exemple :
- dans un histogramme produit avec
hist: les fréquences des observations dans les intervalles, - dans des diagrammes en boîte produits par la fonction
boxplot: les statistiques représentées dans les diagrammes, - etc.
- dans un histogramme produit avec
Exemple d’utilisation des valeurs retournées par la fonction barplot
# Calcul des fréquences
freq_mag_catego <- table(quakes$mag_catego)
# Production du diagramme à barres
out_barplot <- barplot(
height = freq_mag_catego,
xlab = "modalité de magnitude",
ylab = "fréquence",
)
out_barplot## [,1]
## [1,] 0.7
## [2,] 1.9
## [3,] 3.1# Ajout d'annotations textuelles (valeurs des fréquences représentées)
text(
x = out_barplot, # coordonnées en x (centres des bâtons) tirées de out_barplot
y = freq_mag_catego, # coordonnées en y (hauteurs des bâtons) tirées de freq_mag_catego
labels = freq_mag_catego,
pos = c(1, 1, 3) # annotations positionnée sous la coordonnée pour les 2 premiers
) # bâtons, mais au dessus de la coordonnée pour le dernier bâton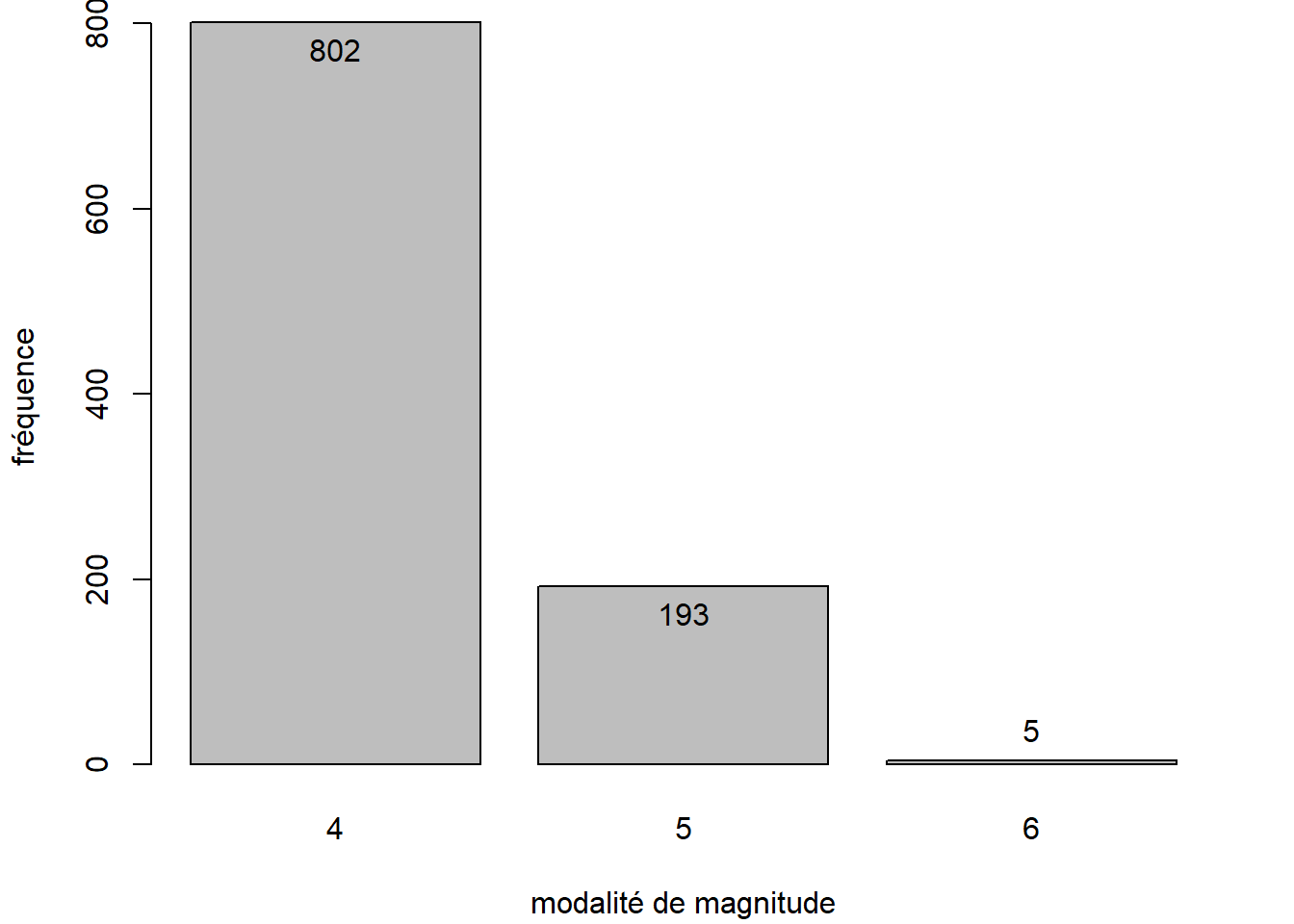
2.9 Point de vue
La fonction générique plot choisit un bon type de graphique à produire selon le nombre et la nature des variables reçues en entrée.
Sinon, les fonctions graphiques de base en R font très peu de choix pour l’utilisateur.
Les graphiques initialisés sont typiquement minimalistes. Nous y ajoutons ce que nous voulons. Et les possibilités sont nombreuses.
- Avantage : Nous avons le plein contrôle sur l’apparence du graphique.
- Désavantage : Il faut parfois travailler fort pour arriver à nos fins.
Faiblesse du système graphique de base
Les représentations multivariées ne sont pas simples à produire. Il n’est pas toujours facile, avec les fonctions graphiques de base, de représenter trois variables et plus sur le même graphique.
Exemple - Représenter deux variables numériques et une variable catégorique
Tentons de représenter la relation entre les variables numériques stations et mag de quakes en fonction de la variable catégorique region.
Option 1 : Sous-fenêtres selon la variable catégorique
Graphiques par niveau du facteur placés côte-à-côte.
par_default <- par(mfrow = c(1,2))
plot(stations ~ mag, data = quakes, subset = region == "Ouest", main = "Region Ouest")
plot(stations ~ mag, data = quakes, subset = region == "Est", main = "Region Est")
par(par_default)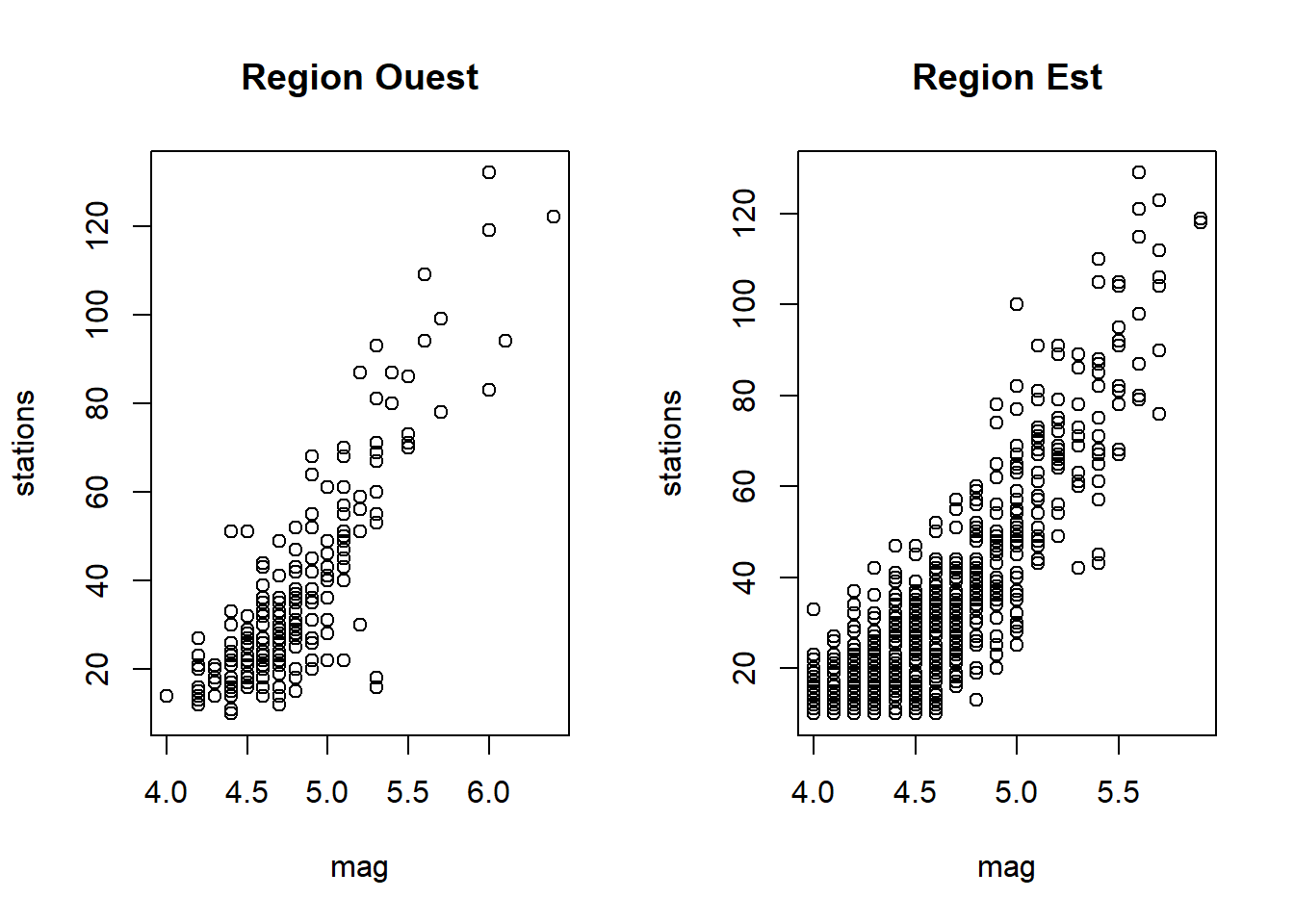
Il faudrait idéalement :
- ajuster les axes afin que tous les graphiques couvrent la même région,
- éviter la redondance dans les noms des axes.
Option 2 : Superposition avec aspect distinctif selon la variable catégorique
Faisons varier le symbole utilisé pour les points et sa couleur selon le niveau du facteur region.
Nous pouvons donner aux arguments graphiques un vecteur de valeurs, plutôt qu’une seule valeur. Ce vecteur doit être de même longueur que le nombre d’observations à représenter (sinon il sera recyclé ou tronqué).
plot(
stations ~ mag, data = quakes,
pch = as.numeric(region), col = as.numeric(region) + 2
)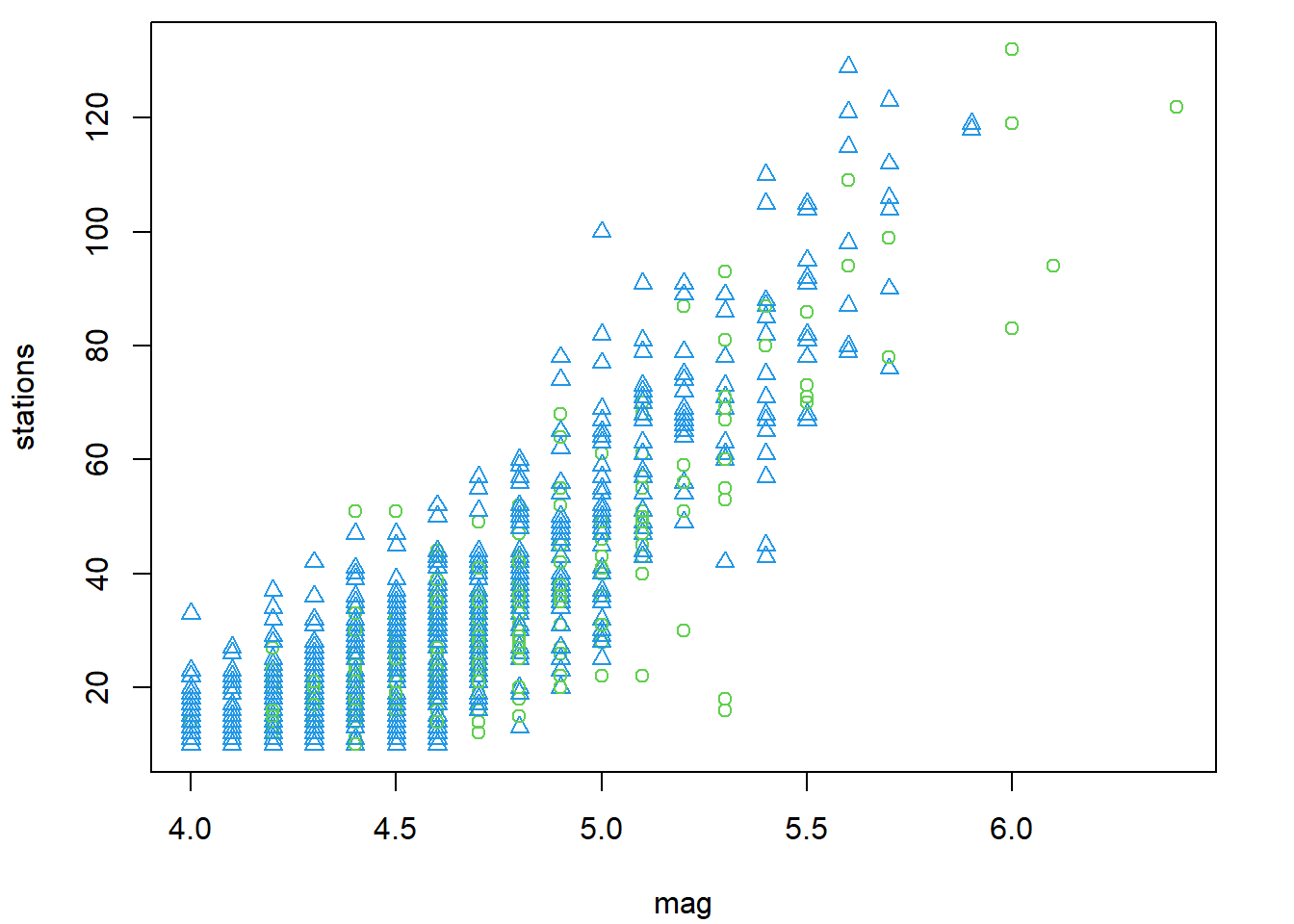
Il faudrait ajouter une légende pour identifier à quoi réfère les couleurs et les symboles.
Notons que nous avions déjà produit un graphique similaire avec matplot. Ce graphique pourrait aussi être produit en ajoutant les points pour chaque groupe dans des étapes séparées, comme suit.
# Initialisation d'un graphique vide, mais avec les bonnes étendues
plot(stations ~ mag, data = quakes, type = "n")
# Ajout des points pour la région Ouest
points(stations ~ mag, data = quakes, subset = region == "Ouest", pch = 1, col = 3)
# Ajout des points pour la région Est
points(stations ~ mag, data = quakes, subset = region == "Est", pch = 2, col = 4)Exemple - Représenter trois variables numériques et une variable catégorique
Tentons maintenant de représenter dans un même graphique les variables suivantes de quakes : lat, long, mag et region.
par_default <- par(pty = "s") # pty = "s" permet d'avoir une région graphique carrée
plot(
lat ~ long, data = quakes,
asp = 1, # asp = 1 permet d'avoir des axes sur la même échelle,
# ce qui est préférable ici, car les variables sont des coordonnées géographiques
cex = 3*(mag - min(mag))/(max(mag) - min(mag)) + 1, pch = 20,
# la taille du symbole dépend de la valeur de la variable mag
col = ifelse(region == "Ouest", rgb(1, 0, 0, 0.3), rgb(0, 0, 1, 0.3))
# la couleur du symbole dépend du facteur région
# des couleurs transparentes sont utilisées
)
par(par_default)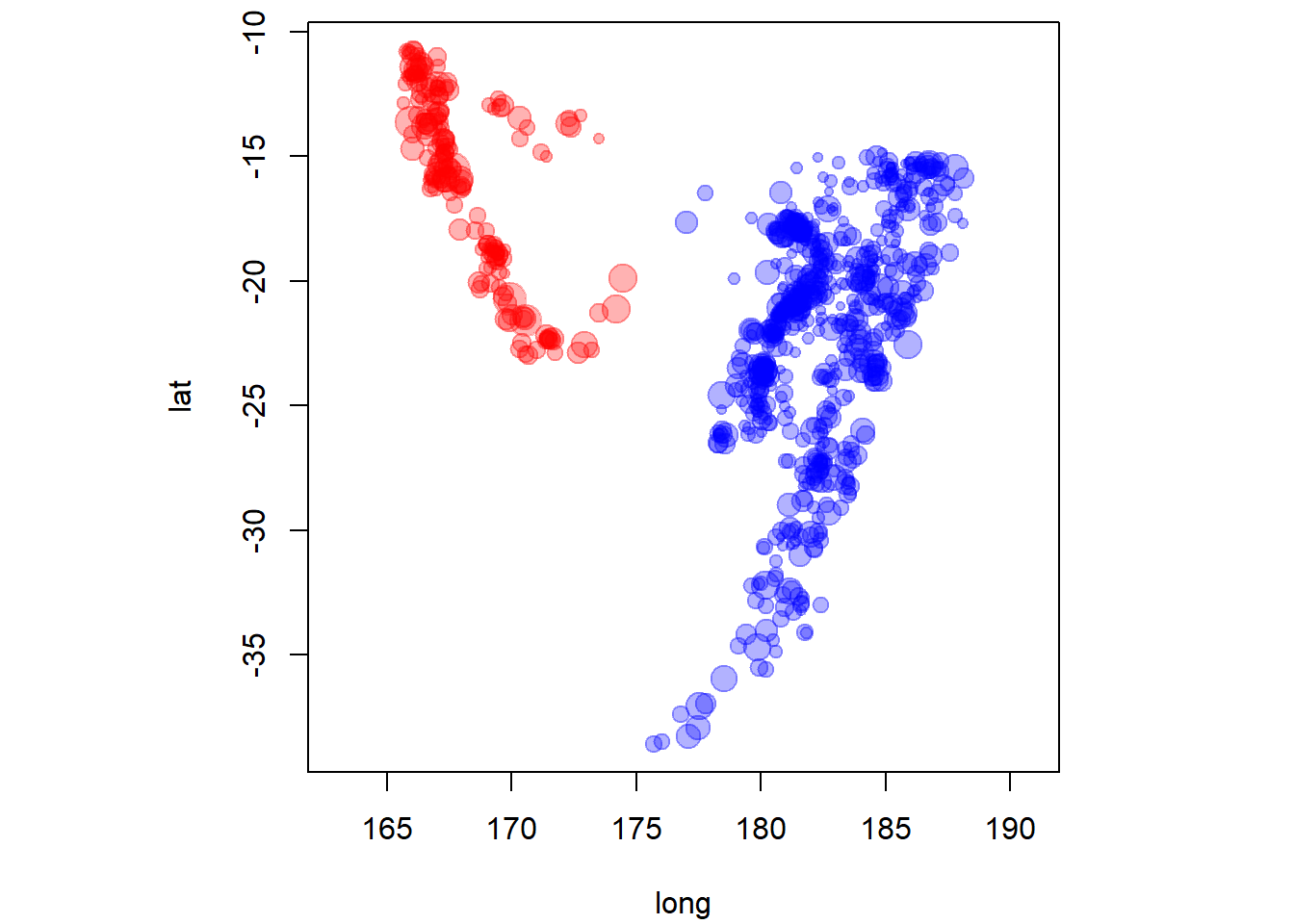
Il faudrait ajouter une légende pour identifier à quoi réfère les couleurs différents (region) et les tailles différentes (mag).
Nous avons réussis à créer des représentations multivariées avec le système graphique de base, mais celles-ci devraient être encore travaillées un peu pour être vraiment adéquates. Les autres systèmes graphiques en R permettent de créer ce genre de graphiques plus rapidement.
3 Package lattice
Le package lattice fut le premier à palier aux faiblesses de R quant aux représentations multivariées. Il a été développé par Deepayan Sarkar et publié pour la première fois en 2001. Il est basé sur le « trellis » système de S-PLUS, qui implémente le système graphique présenté dans : « Cleveland, W. S. (1993). Visualizing data. Hobart Press ». Il permet de facilement produire des graphiques conditionnels à la valeur d’un ou de plusieurs facteurs.
Le package lattice a une importance historique indéniable et a déjà été l’outil de prédilection pour les représentations multivariées en R. Il faut admettre cependant qu’il semble avoir été éclipsé par ggplot2. Pour cette raison, je ne présente ici que quelques exemples d’utilisation de ce package, faisant principalement appel à sa fonction xyplot servant à créer des diagrammes de dispersion. Des ressources pour en apprendre davantage à propos du package lattice sont mentionnées dans les références.
Caractéristiques :
- Les fonctions prennent idéalement une formule en entrée.
- L’opérateur
|sert à créer des grilles de sous-graphiques,- chacun des sous-graphiques est conditionnel à la valeur de facteurs(s), il représente donc seulement le sous-ensemble des observations ayant une modalité particulière pour ce(s) facteur(s).
- L’opérateur
- L’argument
groupssert à superposer des éléments avec un aspect (couleur, forme, taille, etc.) qui varie selon les niveaux d’un facteur. - Un graphique est créé par un seul appel à une fonction du package.
- Les fonctions ont beaucoup de paramètres.
- Il n’est pas possible d’ajouter des éléments à un graphique comme dans le système de base.
# Chargement du package
library(lattice)Exemples : Diagrammes de dispersion - fonction xyplot
Diagramme de dispersion
xyplot(stations ~ mag, data = quakes)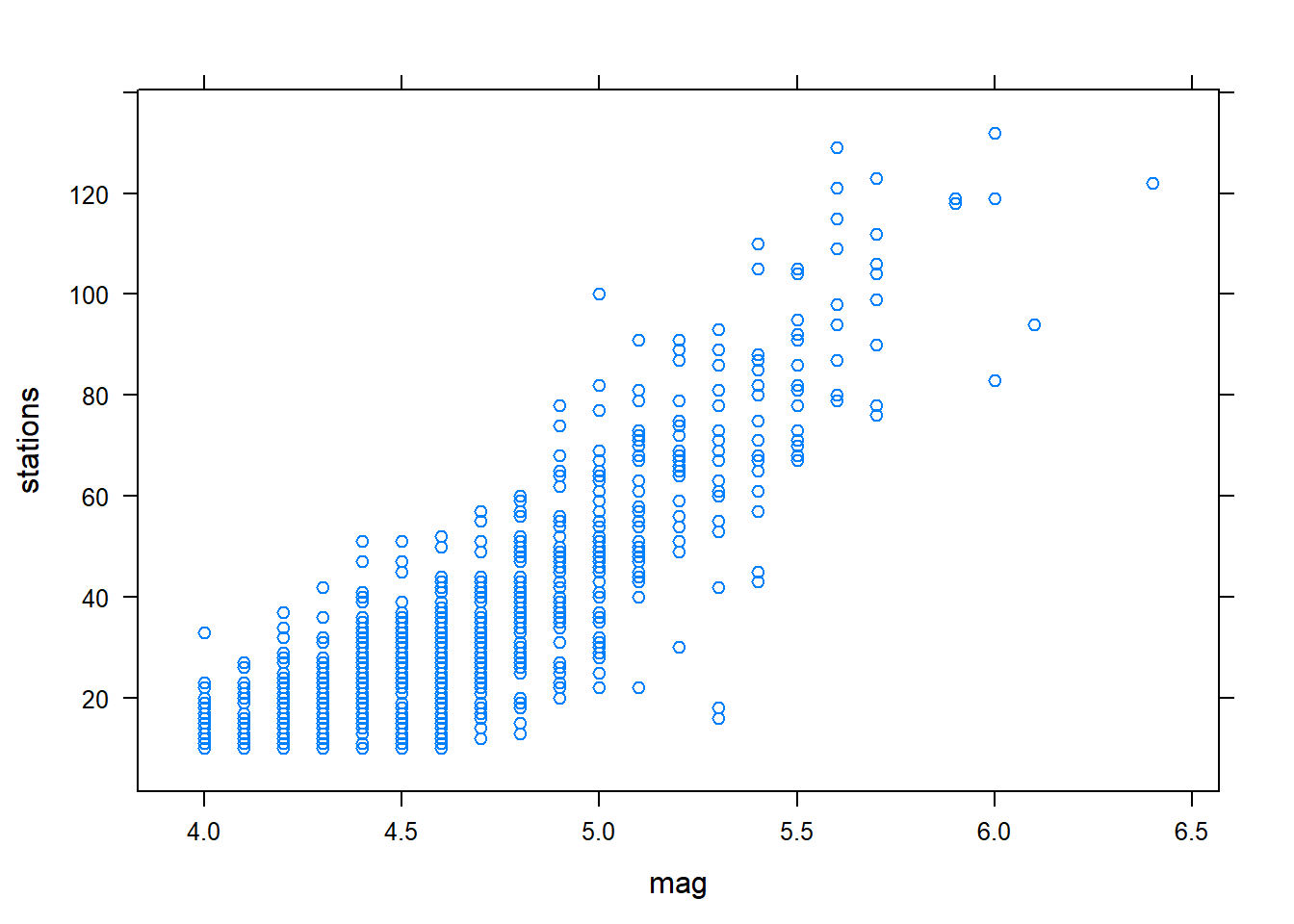
Diagrammes de dipersion juxtaposés
xyplot(stations ~ mag | region, data = quakes)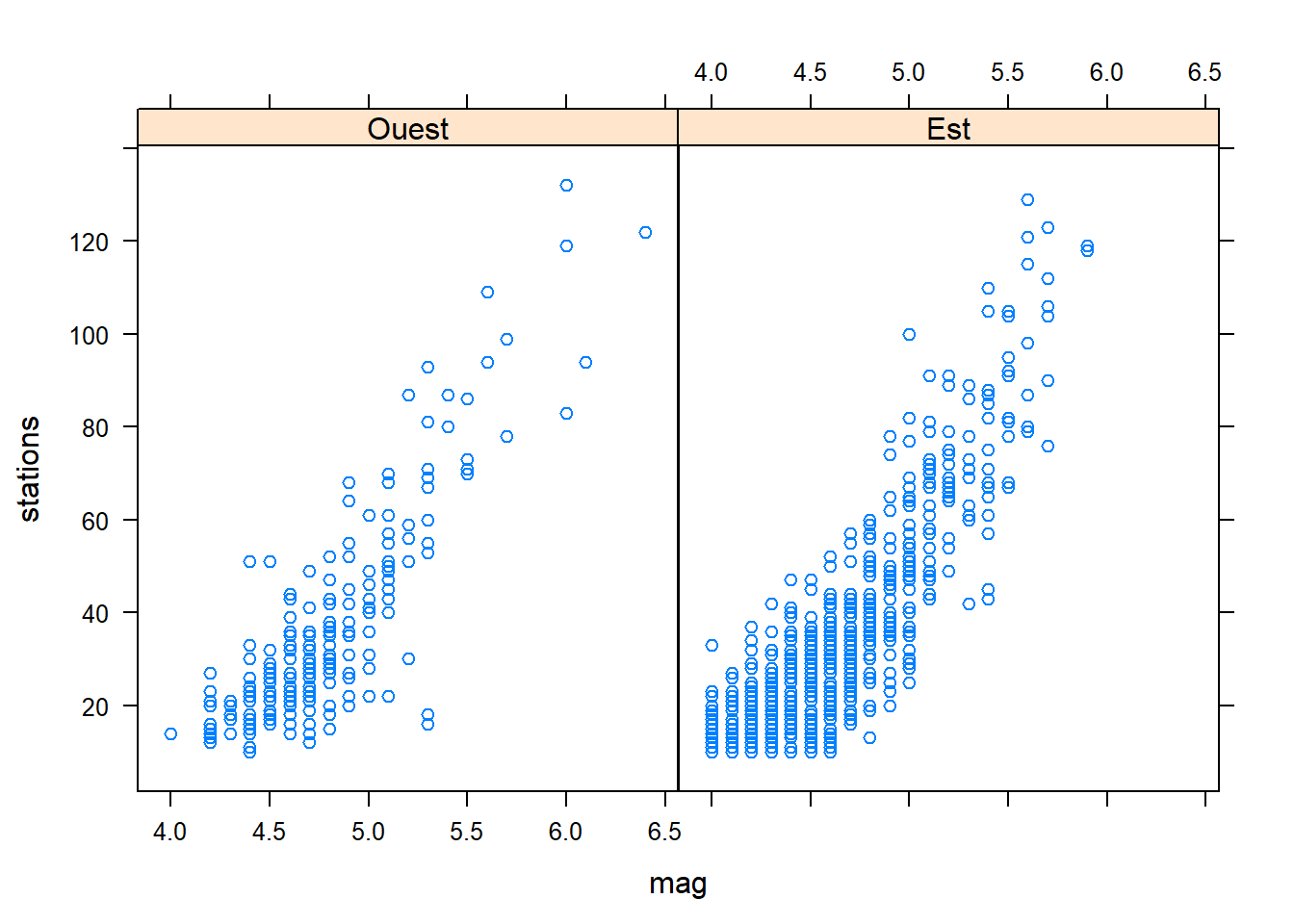
Ajout d’une courbe de lissage
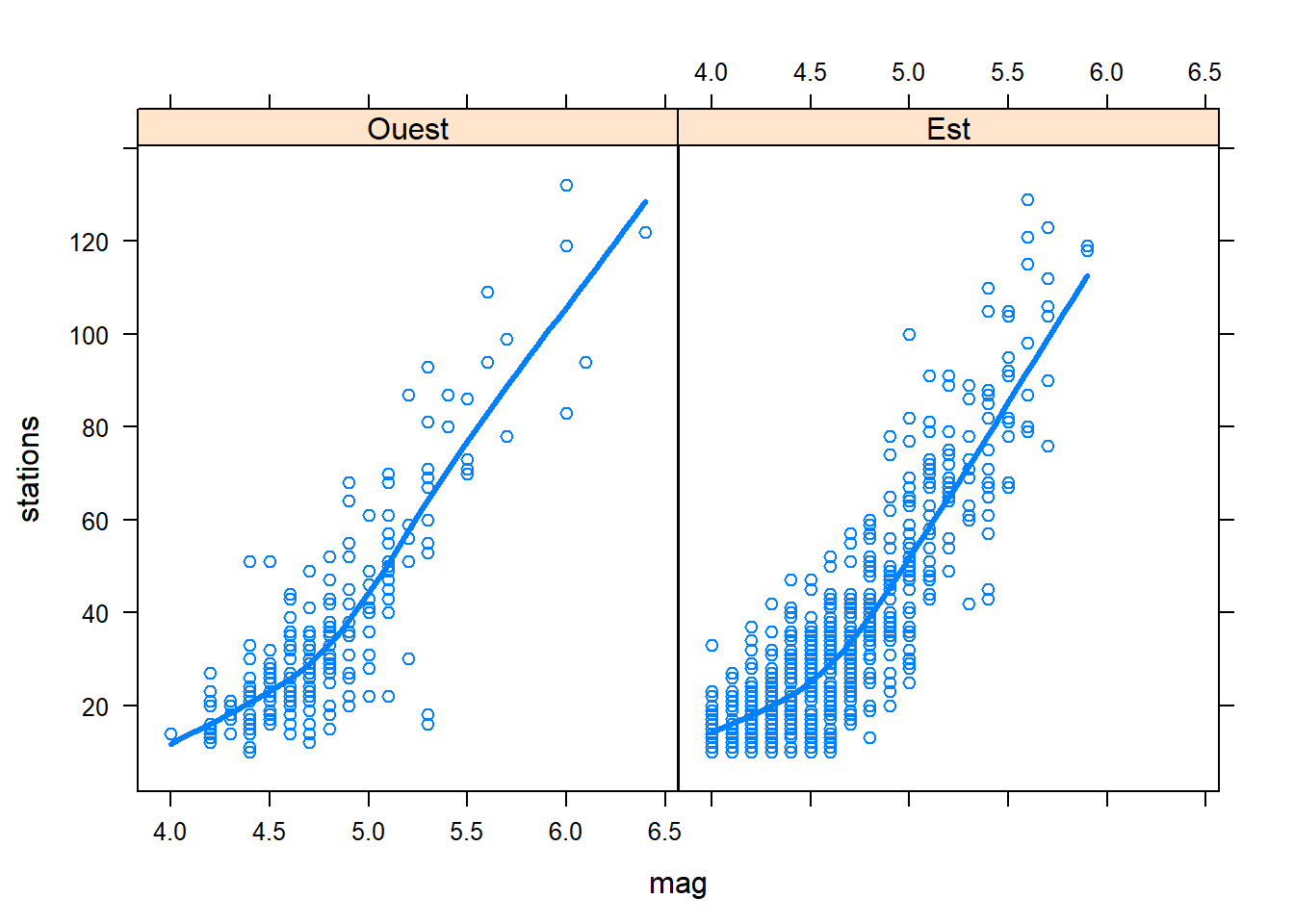
xyplot(
stations ~ mag | region, data = quakes,
type = c("p", "smooth"), lwd = 3
)
Diagrammes de dispersion superposés
xyplot(stations ~ mag, data = quakes, groups = region, auto.key = TRUE)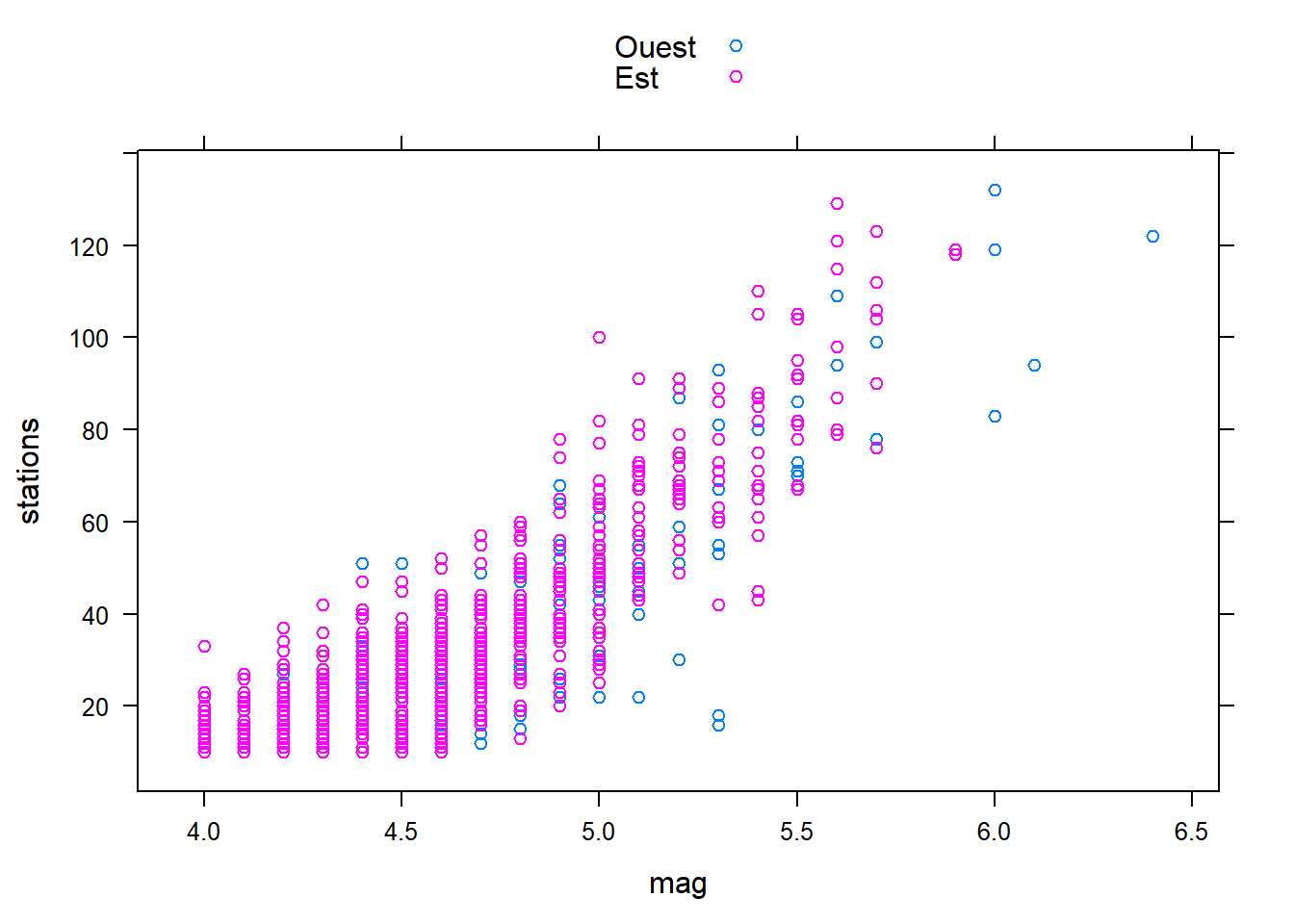
L’argument auto.key permet d’ajouter automatiquement une légende.
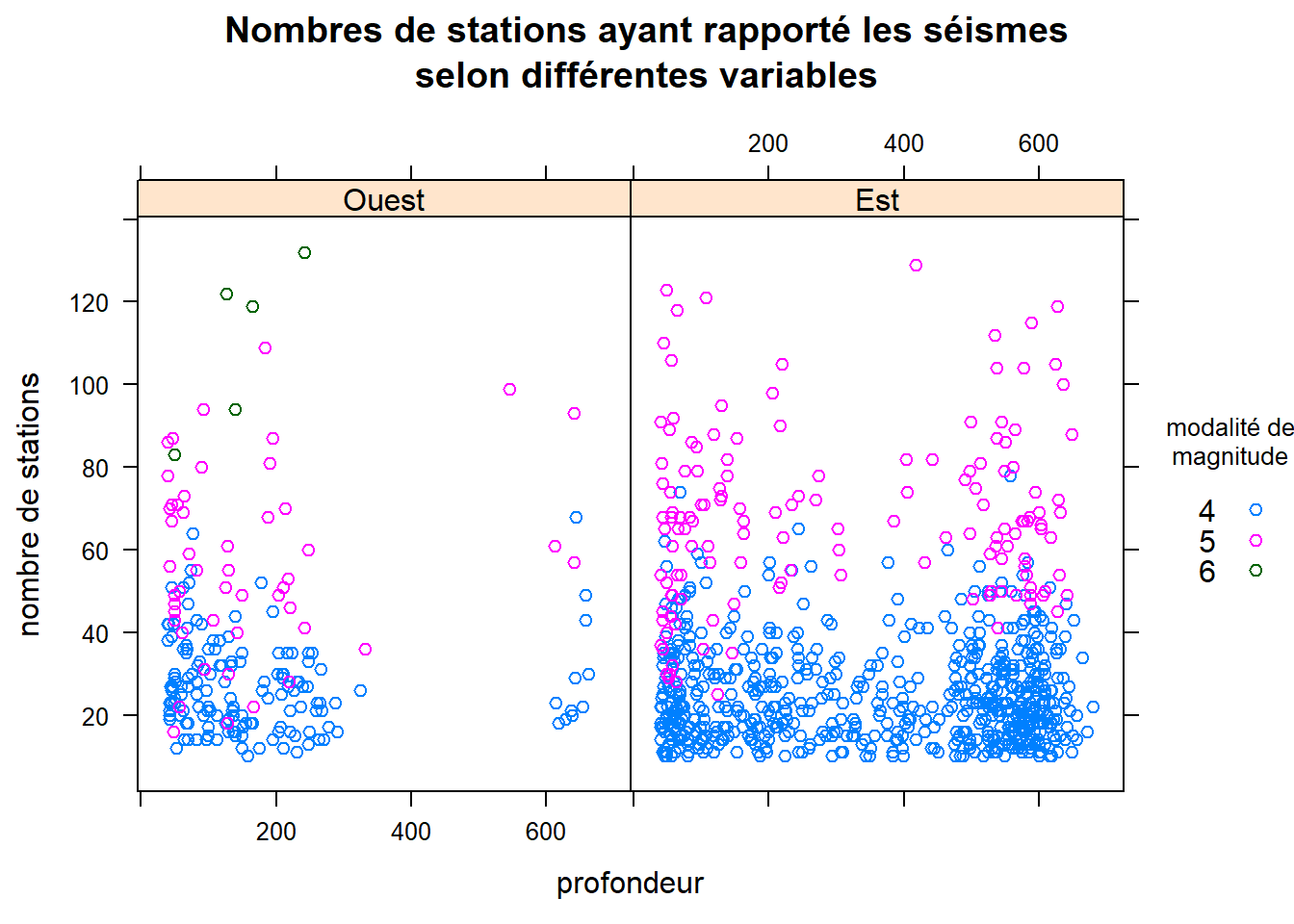
Exemple complet de représentation simultané de quatre variables
xyplot(
stations ~ depth | region, data = quakes, groups = mag_catego,
main = "Nombres de stations ayant rapporté les séismes\nselon différentes variables",
xlab = "profondeur", ylab = "nombre de stations",
auto.key = list(title = "modalité de\nmagnitude", space = "right", cex.title = 0.8)
)
Exemple : Diagramme en points de Cleveland - fonction dotplot
L’auteur du système graphique derrière le package lattice, soit William S. Cleveland, est aussi celui qui a proposé les diagrammes en points pouvant remplacer les diagrammes à barres. Le package lattice possède une fonction pour créer facilement ce type de graphique : la fonction dotplot.
quakes_freq_df <- as.data.frame(xtabs(~ region + mag_catego, data = quakes))
dotplot(
mag_catego ~ Freq, data = quakes_freq_df, groups = region,
xlab = "Fréquence", ylab = "Modalité de magnitude", auto.key = TRUE
)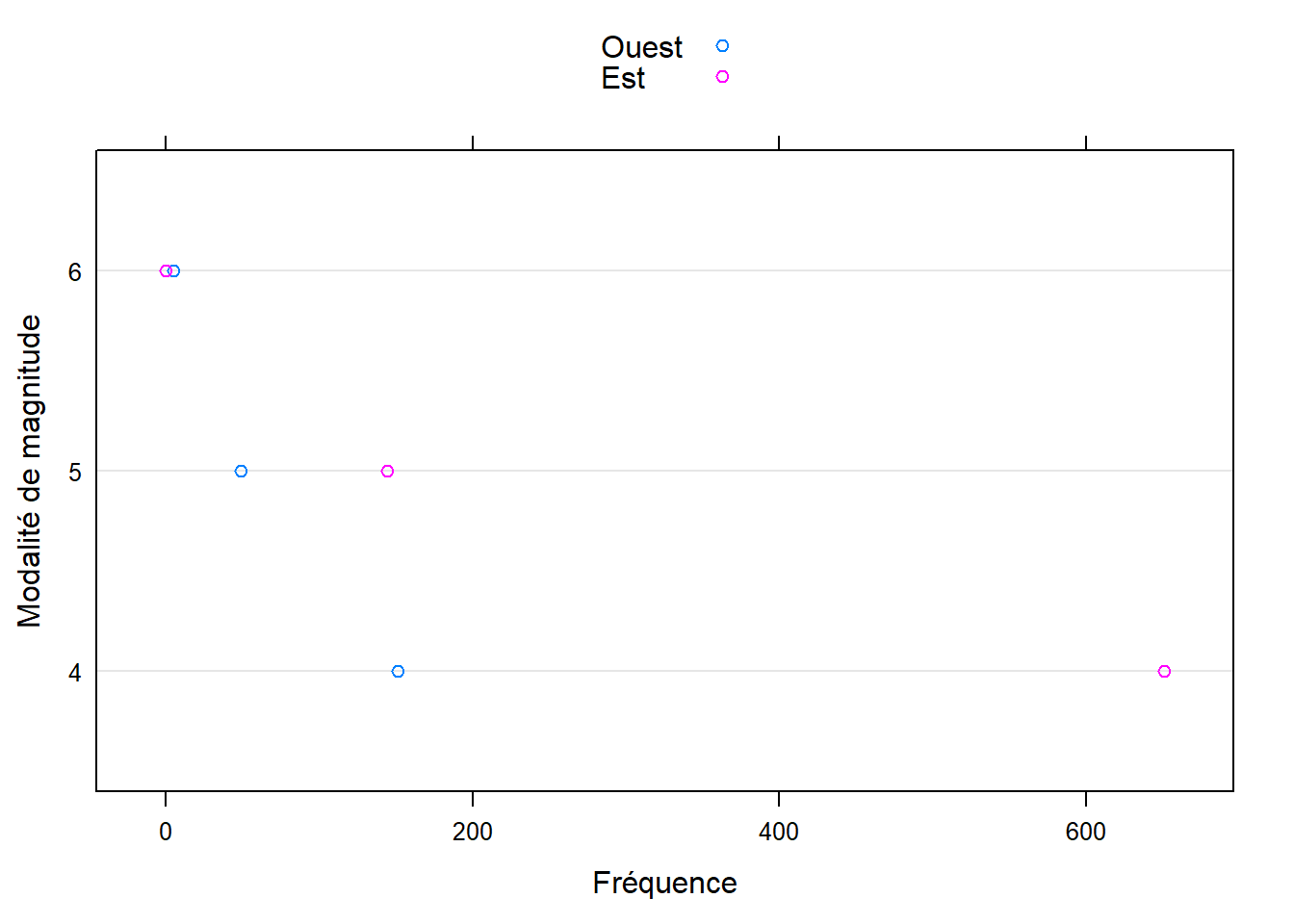
Remarquons que contrairement au diagramme similaire créé précédemment avec la fonction dotchart du système graphique de base, les points pour les deux niveaux de la variable region sont ici placés sur la même ligne, facilitant encore plus la visualisation de la différence entre les deux fréquences associées.
4 Package ggplot2
L’utilisation du package ggplot2 est traitée dans les notes intitulée « Graphiques avec ggplot2 en R » :
https://stt4230.rbind.io/communication_resultats/graphiques_ggplot2_r/
5 Autres possibilités graphiques en R
Les possibilités graphiques en R sont très diverses, notamment grâce à de nombreux packages graphiques offerts sur le CRAN. À titre illustratif, mentionnons ici trois types de représentations graphiques qui peuvent relativement facilement être produites en R : les graphiques 3D, les graphiques interactifs et les cartes géographiques.
5.1 Graphiques 3D
L’utilisation de 3D pour la représentation de données catégoriques est à éviter, car elle nuit à la lisibilité du graphique [5]. Les graphiques 3D peuvent cependant être utiles pour visualiser une surface.
Fonction persp du système de base
Voici un exemple de graphique 3D produit avec la fonction persp du système graphique de base :
x <- y <- seq(from = -1, to = 1, length = 100)
grille <- expand.grid(x = x, y = y)
z <- grille$x^2 + grille$y^2
persp(x = x, y = y, z = matrix(z, ncol = length(x)), zlab = "z")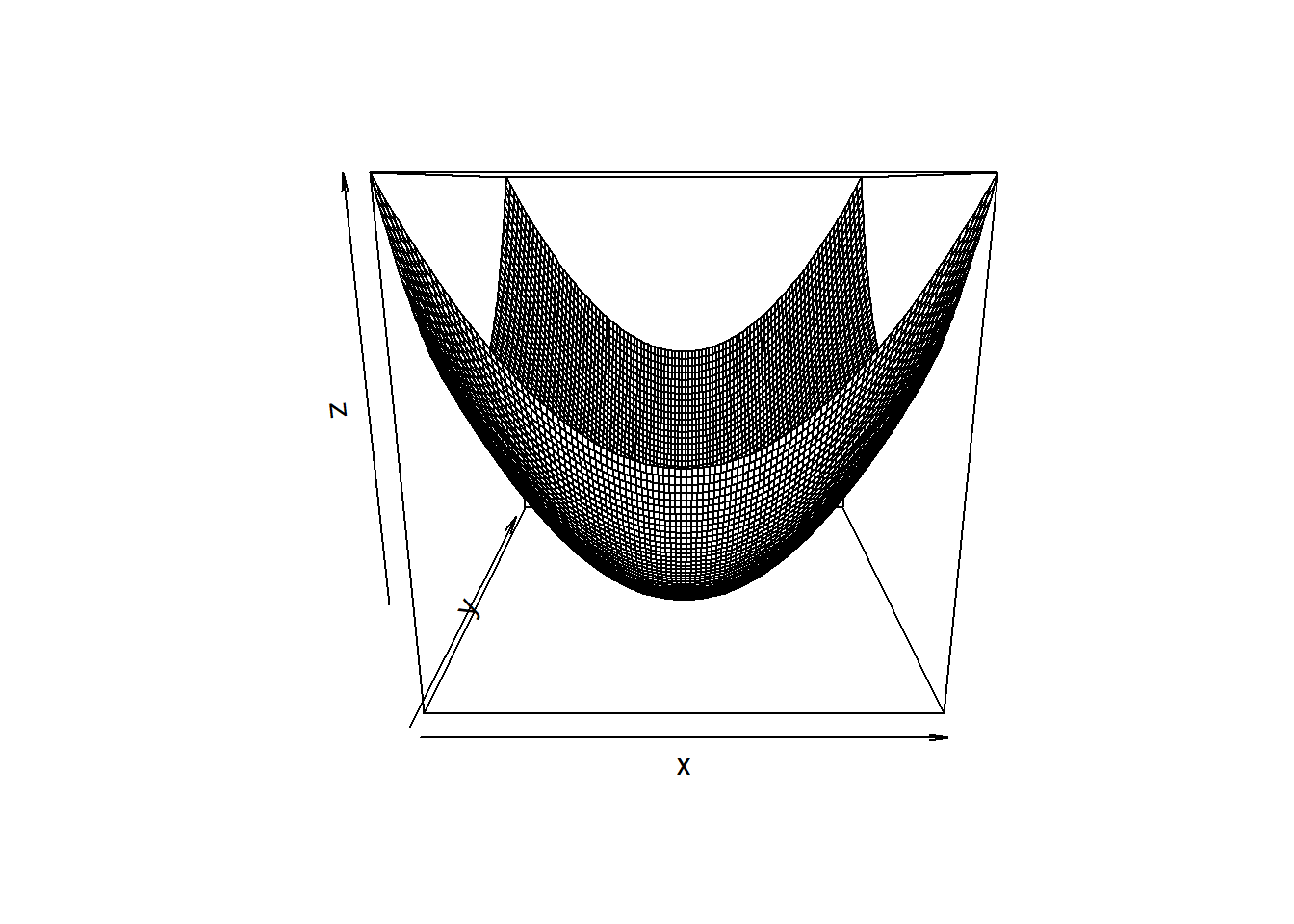
Cette fonction ne permet pas de représenter un diagramme de dispersion (nuage de points) en 3 dimensions. Elle permet plutôt de tracer une fonction mathématique de 2 variables. Il faut fournir à l’argument z la valeur de la fonction mathématique pour toutes les combinaisons des valeurs en x et et y. Les angles de vue du graphique peuvent être contrôlés à l’aide des arguments theta et phi.
Graphiques 3D orientables - package rgl
Le package rgl permet de produire des graphiques 3D orientables, ce qui facilite grandement la visualisation de ce type de graphique. Chaque graphique produit par rgl est affiché dans une fenêtre interactive qui permet à l’utilisateur de faire tourner le graphique dans n’importe quel sens. Des exemples de graphiques produits avec le package rgl peuvent être visualisés dans le tutoriel suivant, réalisé par d’anciens étudiants du cours : https://stt4230.rbind.io/tutoriels_etudiants/hiver_2019/rgl/
5.2 Graphiques interactifs
Un graphique interactif est un graphique qui n’est pas statique (une image fixe), mais qui est plutôt capable d’interagir avec la personne qui l’observe. Les graphiques produits par le package rgl peuvent donc être qualifiés d’interactifs.
La forme la plus simple et usuelle d’interaction est de fournir de l’information supplémentaire lorsque la souris est placée sur certains éléments du graphique. Une forme plus avancée d’interaction est de modifier certains éléments du graphique en fonction de choix fait par l’observateur, par exemple via des boutons ou un menu cliquable.
Ce genre de graphique se visualise typiquement dans un navigateur internet. Il s’intègre facilement à un document HTML (comme une page web), mais pas à un document PDF puisque ce type de document est statique.
Les tutoriels suivants, réalisés par d’anciens étudiants de ce cours, portaient sur des packages R pour la création de graphiques interactifs. Pour voir des exemples de graphiques interactifs, vous pouvez allez consulter ces tutoriels. Le package abordé dans le premier tutoriel de cette liste est particulièrement intéressant. Il permet de créer facilement en R des graphiques Plotly (https://plot.ly/), une application web de production de graphiques interactifs très populaire.
- package
plotlymentionné ci-dessus :
https://stt4230.rbind.io/tutoriels_etudiants/hiver_2018/plotly/ - package
googleVispour créer des Google charts :
https://stt4230.rbind.io/tutoriels_etudiants/hiver_2018/googlevis/ - package
highcharterbasé sur la librairie JavaScript Highcharts, pour produire divers graphiques interactifs :
https://stt4230.rbind.io/tutoriels_etudiants/hiver_2018/highcharter/ - package
ggiraphpour rendre des graphiquesggplot2interactifs :
https://stt4230.rbind.io/tutoriels_etudiants/hiver_2018/ggiraph/ - package
dygraphs, basé sur la librairie JavaScript du même nom, pour produire des graphiques temporels interactifs : https://stt4230.rbind.io/tutoriels_etudiants/hiver_2019/dygraphs/
Mentionnons en terminant que les applications Shiny, développés par RStudio, permettent aussi de rendre n’importe quel graphique R interactif. Ces applications sont très bien documentées ici : https://shiny.rstudio.com/
5.3 Cartes géographiques
Il est possible de créer des cartes géographiques avec R. Sans entrer dans les détails les références suivantes présentent divers packages R pour la création de cartes :
- package
maps(au besoin avecmapdataetmapproj) - package
leaflet: permet de créer des cartes interactives avec la librairie JavaScript du même nom https://leafletjs.com/- tutoriel réalisé par un ancien étudiant du cours : https://stt4230.rbind.io/tutoriels_etudiants/hiver_2020/leaflet/
- package
cartography: permet de créer différentes représentations cartographiques en R - package
tmap: permet notamment de facilement créer des cartes choroplèthes (cartes géographiques intégrant des couleurs dans des régions selon le niveau d’une variable) - package
ggmap: permet d’intégrer une carte Google Maps (requière un compte sur https://cloud.google.com/maps-platform/ pour avoir accès aux cartes) ou Stamen Maps à un graphique produit avecggplot2 - package
sf: manipulation de données spatiales - Références mentionnant divers packages R pour la production de cartes géographiques :
- CRAN task view : https://CRAN.R-project.org/view=Spatial
- Blogue bilingue (anglais/français) : https://statnmap.com/fr/
- Chapitre d’un livre web : https://geocompr.robinlovelace.net/adv-map.htm
Package maps
Des packages énumérés ci-dessus, le plus simple d’utilisation (mais pas le plus puissant) est probablement le package maps. Voici un petit exemple d’utilisation de la fonction map du package maps avec les données quakes.
library(maps)
map(
database = "world",
fill = TRUE, col = "gray90",
xlim = c(115, 190), ylim = c(-50, 0)
)
points(
x = quakes$long, y = quakes$lat,
pch = 20, col = rgb(0, 0, 1, 0.3)
)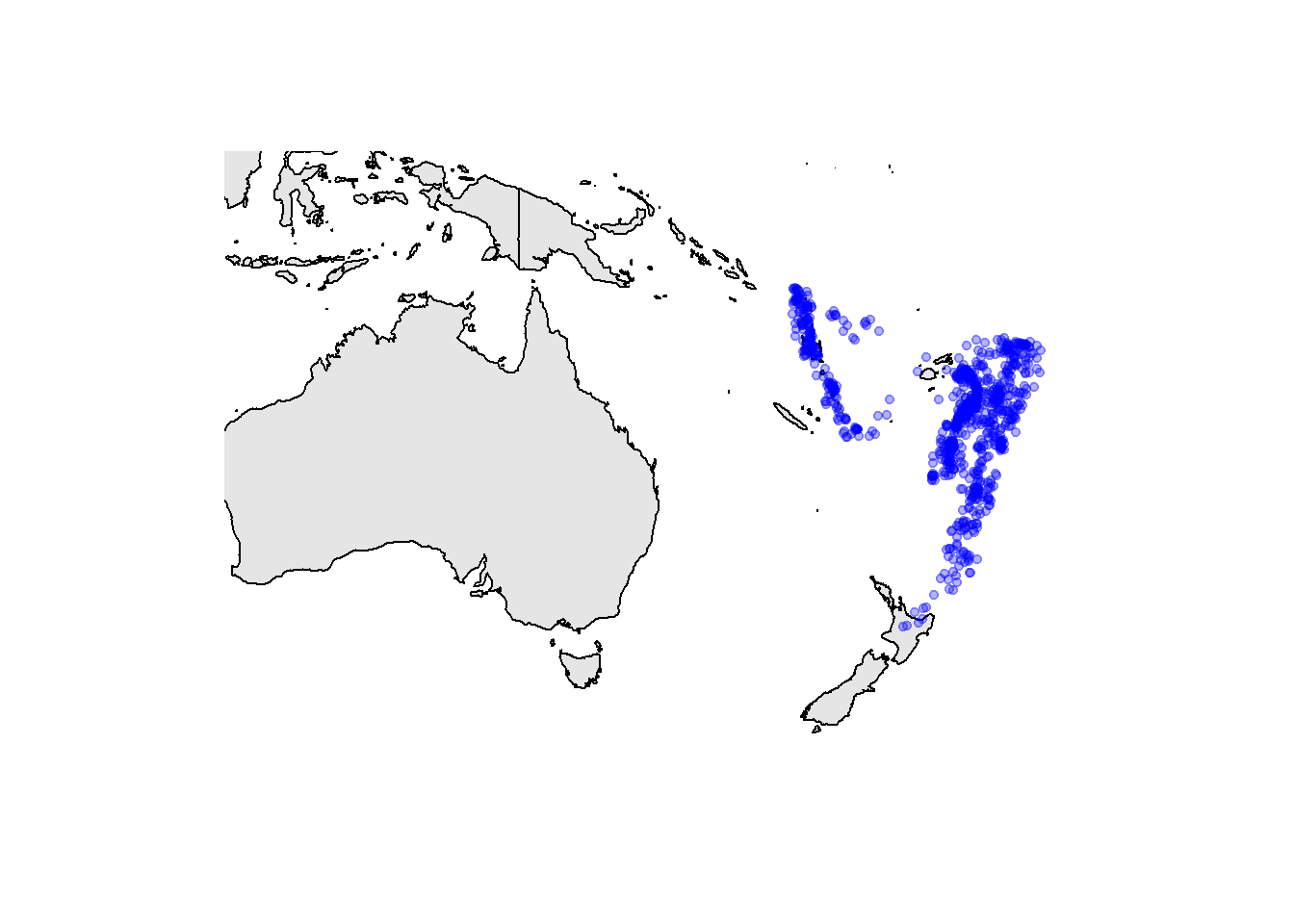
Le package maps fournit des banques de données géographiques, tel que la carte nommée world utilisée ci-dessus. Au besoin, encore plus de cartes sont accessibles par l’intermédiaire du package mapdata. Également, la fonction map utilise par défaut une projection cartographique rectangulaire. Le package mapproj fournit d’autres projections (p. ex. la projection de Mercator).
6 Conclusion
En conclusion, R est un excellent outil pour produire toutes sortes graphiques. Il peut s’agir de graphiques vite faits pour explorer rapidement des données ou encore de graphiques longuement travaillés afin de les configurer pour des besoins précis. Des graphiques de très bonne qualité peuvent ainsi être créés en R et intégrés à des publications officielles. De plus, la variété des graphiques possibles à créer en R est impressionnante. De nouvelles fonctions graphiques font fréquemment leur apparition dans des packages distribués sur le CRAN ou ailleurs.
Pour produire des graphiques en R, on procède parfois par essais/erreurs jusqu’à l’obtention du graphique souhaité. D’autres fois, on crée des graphiques R à partir du code source d’un modèle : ce peut être du code que nous avons déjà écrit ou encore un code de création de graphique trouvé dans un livre ou sur internet. Les graphiques R sont facilement reproductibles à partir de leur code source. Et pour connaître toutes les possibilités des fonctions graphiques que nous utilisons, le meilleur endroit est bien souvent la fiche d’aide de la fonction.
7 Résumé
Packages graphiques en R
Système graphique de base : graphics et grDevices : intégrés au R de base ⇒ chargés par défaut lors de l’ouverture d’une session R
Autres systèmes graphiques :
lattice: emphase sur les représentations multivariéesggplot2: conçu en ayant comme objectif la simplicité d’utilisation et la qualité des graphiques produits
Autres packages permettant de créer divers types de graphiques :
rgl (graphiques 3D orientables), plotly (graphiques interactifs), maps, etc. (Il en existe beaucoup!)
Système graphique de base
Procédure de création d’un graphique de base
- La configuration des paramètres graphiques (au besoin) :
- L’initialisation d’un graphique :
- L’ajout séquentiel d’éléments au graphique (au besoin) :
Arguments et paramètres graphiques ⇒ mise en forme et annotations
Fonction plot
- Fonction générique qui possède plusieurs méthodes :
- Le comportement de
plotdépend de la classe de l’objet assigné à son premier argument.
- Le comportement de
- Choix de
plot= bon type de graphique à produire selon le nombre et la nature des variables. - Observations numériques de deux variables en entrée ⇒ diagramme de dispersion.
Autres fonctions de création d’un graphique
Représentations d’une variable (observations stockées dans x) :
| Type de graphique | Exemple d’appel de fonction | Type de x |
|---|---|---|
| diagramme en secteurs (pie chart) | pie(table(x), ...) |
facteur |
| diagramme à barres (bar plot) | barplot(table(x), ...) |
facteur |
| diagramme en points de Cleveland | dotchart(table(x), ...) |
facteur |
| histogramme | hist(x, ...) |
vecteur numérique |
| courbe de densité à noyau (kernel density plot) | plot(density(x), ...) → méthode plot.density |
vecteur numérique |
| diagramme en boîte (boxplot) | boxplot(x, ...) |
vecteur numérique |
| diagramme quantile-quantile théorique normal | qqnorm(x, ...) |
vecteur numérique |
Représentation d’une expression mathématique : curve(expr, ...)
Représentations de deux variables (observations stockées dans x et y) :
| Type de graphique | Exemple d’appel de fonction | Type de x |
Type de y |
|---|---|---|---|
| diagramme à barres empilées ou groupées | barplot(table(x, y), ...) avec beside = TRUE pour barres groupées |
facteur | facteur |
| diagramme en points de Cleveland | dotchart(table(x, y), ...) |
facteur | facteur |
| diagramme en mosaïque | mosaicplot(table(x, y), ...) |
facteur | facteur |
| diagrammes en boîte juxtaposés | boxplot(y ~ x, ...) |
facteur | vecteur numérique |
| diagramme de dispersion (scatterplot) ou en lignes (line chart) | plot(x, y, ...) → méthode plot.default |
vecteur numérique | vecteur numérique |
| diagramme quantile-quantile empirique | qqplot(x, y, ...) |
vecteur numérique | vecteur numérique |
Représentation de plus de trois variables numériques :
- matrice de diagrammes de dispersion :
pairs( ~ x + y + z, ...) - diagrammes de dispersion superposés :
matplot(matriceX, matriceY, ...)
Arguments et paramètres graphiques
- Arguments communs à plusieurs fonctions graphiques :
- titre et noms d’axes :
main,sub,xlab,ylab; - étendue numérique couverte :
xlim,ylim; - type de représentation :
type.
- titre et noms d’axes :
- Paramètres graphiques :
- autour de la zone graphique :
ann,bty; - orientation des étiquettes des axes :
las; - style des éléments :
lty,lwd,pch; - police de caractères :
font,font.main,font.sub,font.axis,font.lab,family; - grosseur des éléments :
cex,cex.main,cex.sub,cex.axis,cex.lab; - couleur des éléments :
col,col.main,col.sub,col.axis,col.lab,bg; - argument de la fonction
paruniquement :- disposition des graphiques :
mfrowoumfcol,new; - largeur des marges :
mar,oma; - etc.
- disposition des graphiques :
- autour de la zone graphique :
Ajout d’éléments à un graphique
| Fonction(s) R | Élément(s) ajouté(s) |
|---|---|
points et matpoints |
points selon des coordonnées |
lines et matlines |
segments de droites reliant des points |
abline |
droites traversant toute la zone graphique |
segments |
segments de droites entre des paires de coordonnées |
arrows |
flèches entre des paires de coordonnées |
rect |
rectangles |
polygon |
polygones quelconques |
legend |
légende |
text |
texte dans la zone graphique |
mtext |
texte dans la marge |
title |
titre |
axis |
axe |
box |
boîte autour de la zone graphique |
qqline |
ligne dans un graphique quantile-quantile théorique |
Exemple de code avec le système graphique de base
# Configuration de paramètres graphiques
par_default <- par(bty="n", mar = c(5, 5, 4, 2))
# Initialisation du graphique
plot(
x = quakes$mag, y = quakes$stations,
main = "1000 séismes près de Fidji",
xlab = "magnitude du séisme",
ylab = "nombre de stations rapportant le séisme"
)
# Ajout d'une droite de régression
lm_out <- lm(stations ~ mag, data = quakes)
abline(lm_out)
# Réattribution des valeurs par défaut aux paramètres graphiques
par(par_default)Possibilités graphiques dans le R de base
Annotations mathématiques :
- Utilisation de la fonction
expressionousubstitute, parfois accompagnée de la fonctionpaste, avec la syntaxe détaillée dans la fiche d’aideplotmathpour créer les valeurs attribuées aux arguments d’éléments textuels dans un graphique (ex.main,xlab,ylab,labels,legend,text, etc.).
Plusieurs graphiques dans une même fenêtre :
division de la fenêtre en sous-fenêtres
Aspects techniques des graphiques en R
Générer un graphique = soumettre le programme de création
Fenêtre graphique :
- tous les graphiques sont créés dans la même fenêtre,
- RStudio conserve un historique des graphiques produits,
- une nouvelle fenêtre graphique s’ouvre avec la commande
windows()(Windows),quartz()(Mac) ouX11()(Linux).
Enregistrer un graphique :
- par le menu de la fenêtre graphique ou
- avec une fonction
bmp,postscript,pdf,png,tiff,svgoujpeg, selon le format désiré.
Pour fermer une connexion avec une fenêtre graphique ou un fichier
→ dev.off().
Références
Références citées dans le texte :
Références supplémentaires :
Système de base :
- R Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/
- Les fiches d’aides des fonctions graphiques décrivent toutes leus possibilités.
- Tutoriels web :
- Livre : Murrell, P. (2011). R Graphics, Second Edition. CRC Press. URL pour le code R : https://www.stat.auckland.ac.nz/~paul/RG2e/
- Feuilles de triche (cheat sheets) :
Package lattice :
- Page web sur le CRAN : https://CRAN.R-project.org/package=lattice
- Documentation en ligne : http://lattice.r-forge.r-project.org/
- Livre accompagnant le package : Sarkar, D. (2008). Lattice: Multivariate Data Visualization With R. Springer Science & Business Media. URL pour le code R : http://lmdvr.r-forge.r-project.org
- Livre proposant le système graphique implémenté dans le package : Cleveland, W. S. (1993). Visualizing Data. Hobart Press.
Références non spécifiques à un seul système graphique :
- Site web qui guide dans le choix du graphique le plus approprié à réaliser en fonction de nos données et de l’information que nous souhaitons transmettre (avec exemple en R et Python) : https://www.data-to-viz.com/
- Livre sur la visualisation de données : Healy, K. (2018). Data Visualization: A Practical Introduction. Princeton University Press. URL https://socviz.co/
- Site web fournissant de l’information à propos de différents types de graphique : https://datavizcatalogue.com/index.html
- Conseil dans la création de graphiques : https://moz.com/blog/impactful-data-storytelling
- Exemples de graphiques (tous systèmes, mais beaucoup de
ggplot2) avec leur code source permettant de les reproduire : http://www.r-graph-gallery.com/
Annexe
Graphiques produits par plot selon les types d’objets donnés en entrée aux arguments x et y
Voici quelques essais pour mieux comprendre la fonction plot. Appelons la fonction en lui fournissant en entrée des arguments x et y de différentes classes et observons le résultat. Les données quakes sont utilisées ici.
Un seul vecteur numérique
plot(x = quakes$mag)
Si seulement un vecteur est fourni en entrée, en argument x, et qu’aucun argument y n’est fourni, alors les observations contenues dans le vecteur sont placées sur l’axe des y (ordonnées), et les entiers 1 à length(x) sont placés sur l’axe des x (abscisses). C’est la méthode plot.default qui a tracé ce graphique.
Deux vecteurs numériques
plot(x = quakes$mag, y = quakes$stations)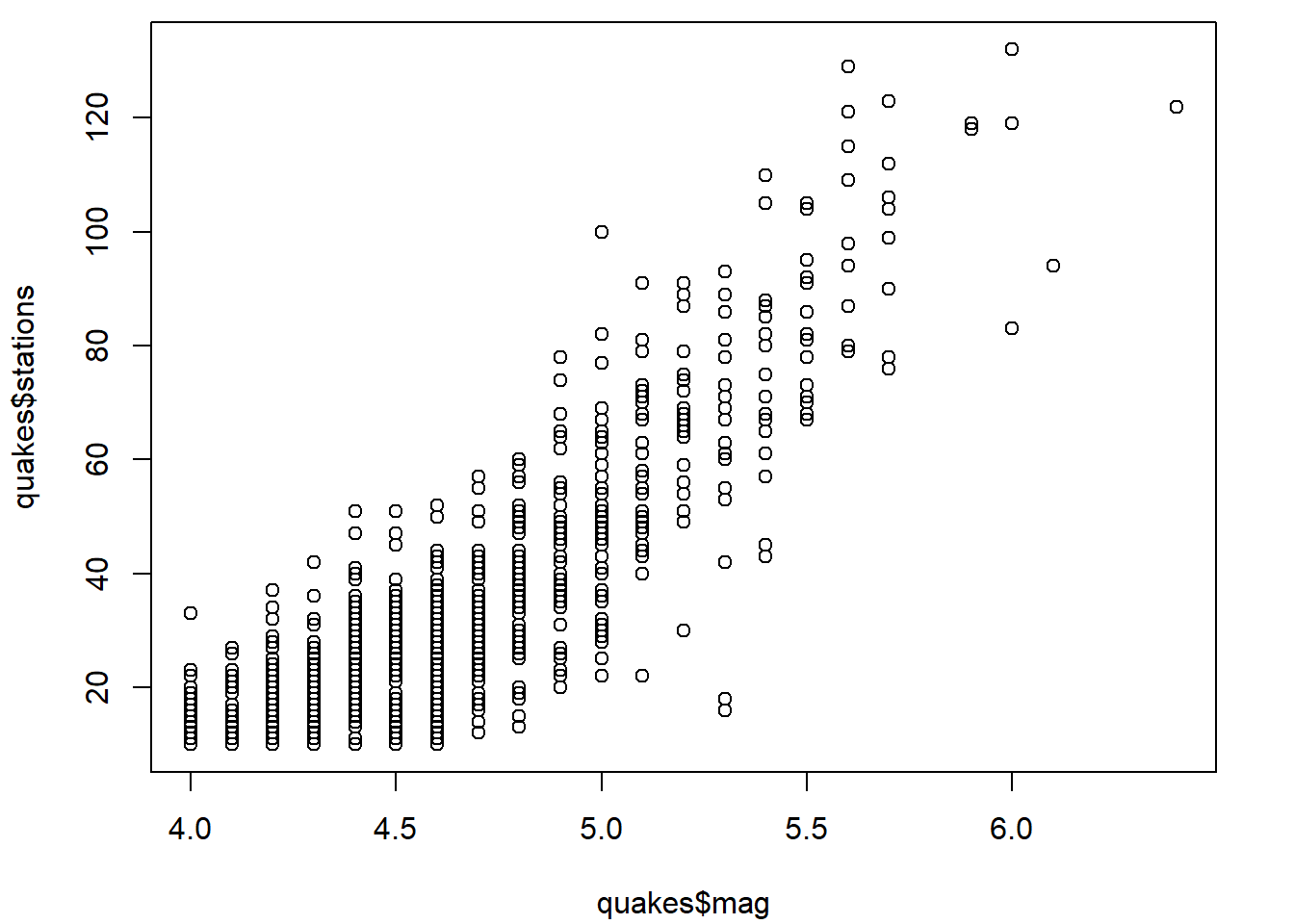
Un diagramme de dispersion est produit, encore par la méthode plot.default.
Un seul facteur
plot(x = quakes$mag_catego)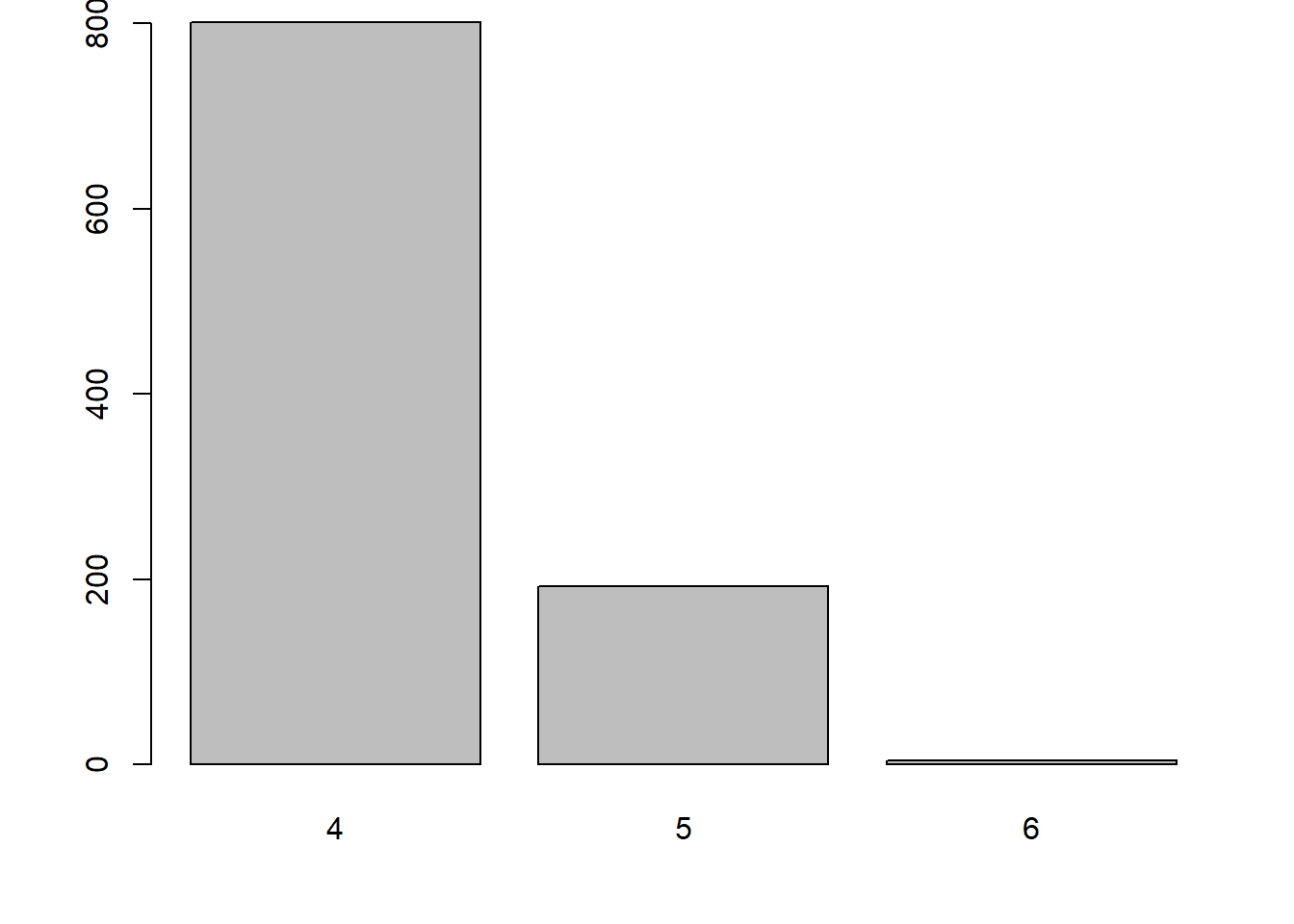
Si seulement un facteur est fourni en entrée, un diagramme à barres est produit. La fonction générique plot a commencé par envoyer les arguments qu’elle a reçus à la méthode plot.factor parce que la classe de l’argument x fourni en entrée était factor. Ensuite, la méthode plot.factor a choisi d’appeler la fonction barplot, parce qu’aucun argument y n’a été fourni. En fait, ce sont les fréquences des niveaux du facteur (table(x)) qui sont données comme premier argument à barplot.
Ainsi, les arguments acceptés par la fonction générique plot lorsqu’elle reçoit en entrée comme premier argument (x) un facteur sans recevoir d’argument y sont les arguments acceptés par la fonction barplot. Par exemple, nous pourrions produire un diagramme à barres horizontales comme suit.
plot(x = quakes$mag_catego, horiz = TRUE)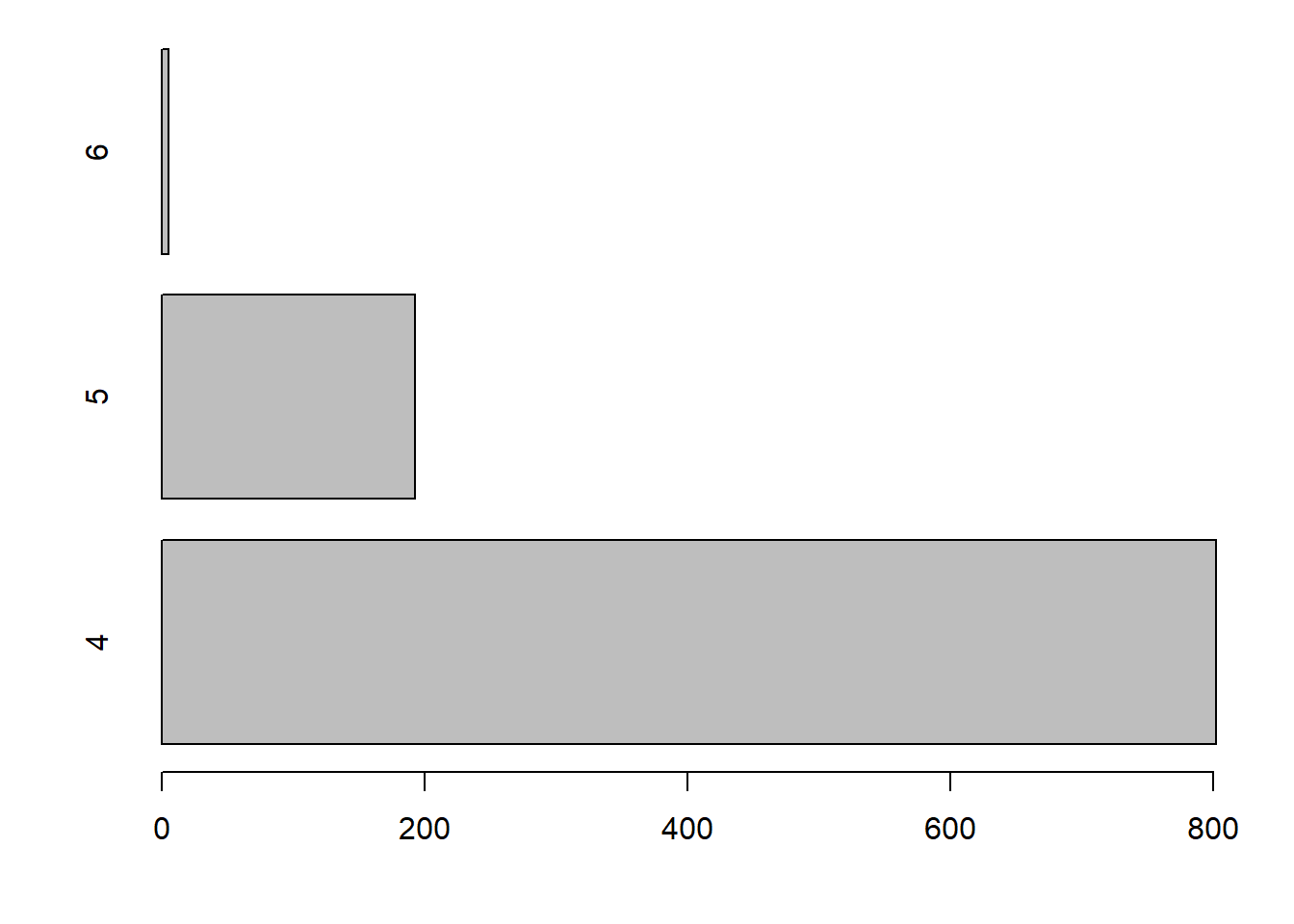
Un facteur et un vecteur numérique
plot(x = quakes$mag_catego, y = quakes$stations)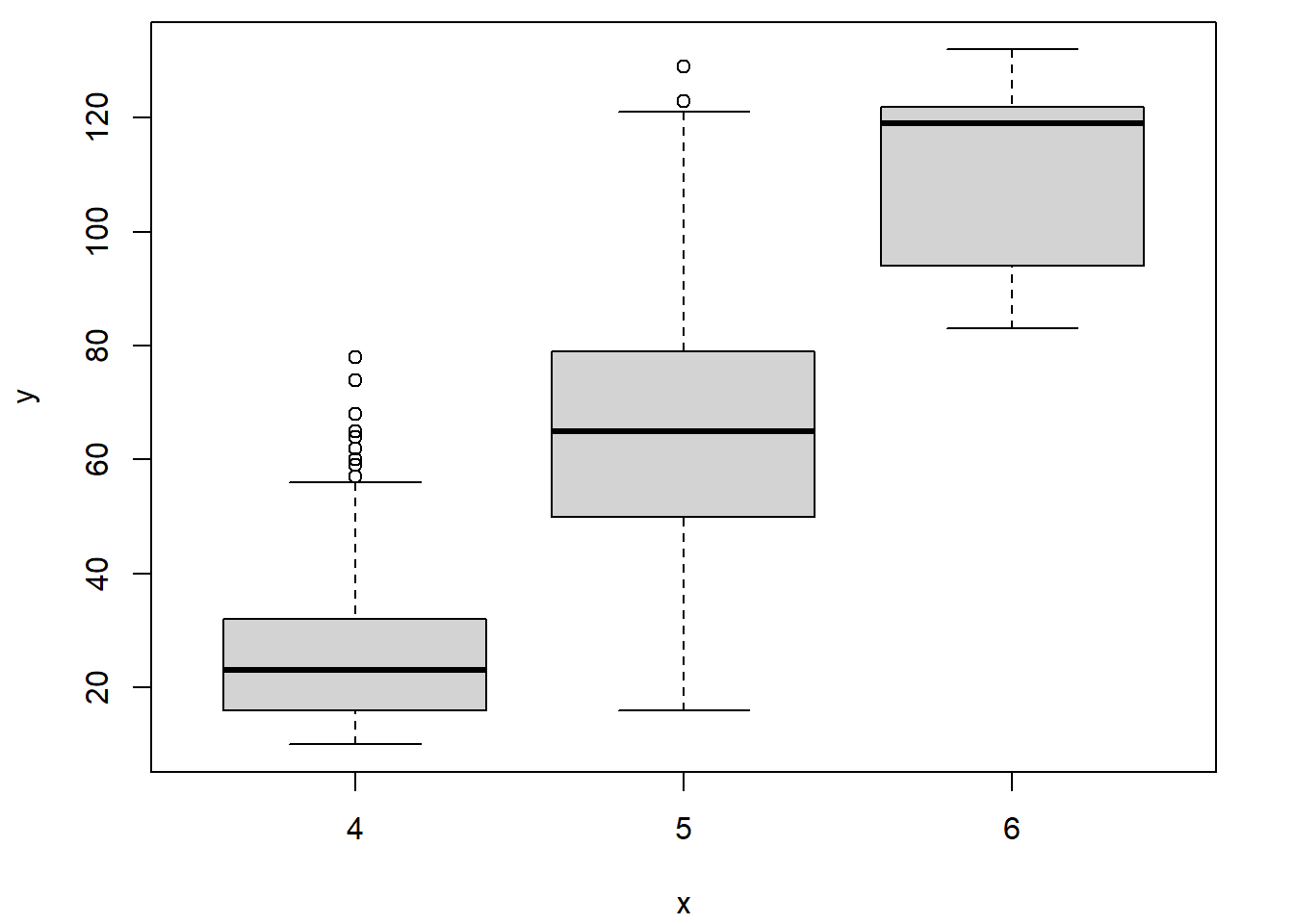
Si un vecteur numérique est fourni en argument y, avec le facteur fourni en x, la méthode plot.factor choisit d’appeler la fonction boxplot pour produire des diagrammes en boîtes de la variable y pour chacun des niveaux de la variable x.
Deux facteurs
plot(x = quakes$mag_catego, y = quakes$region)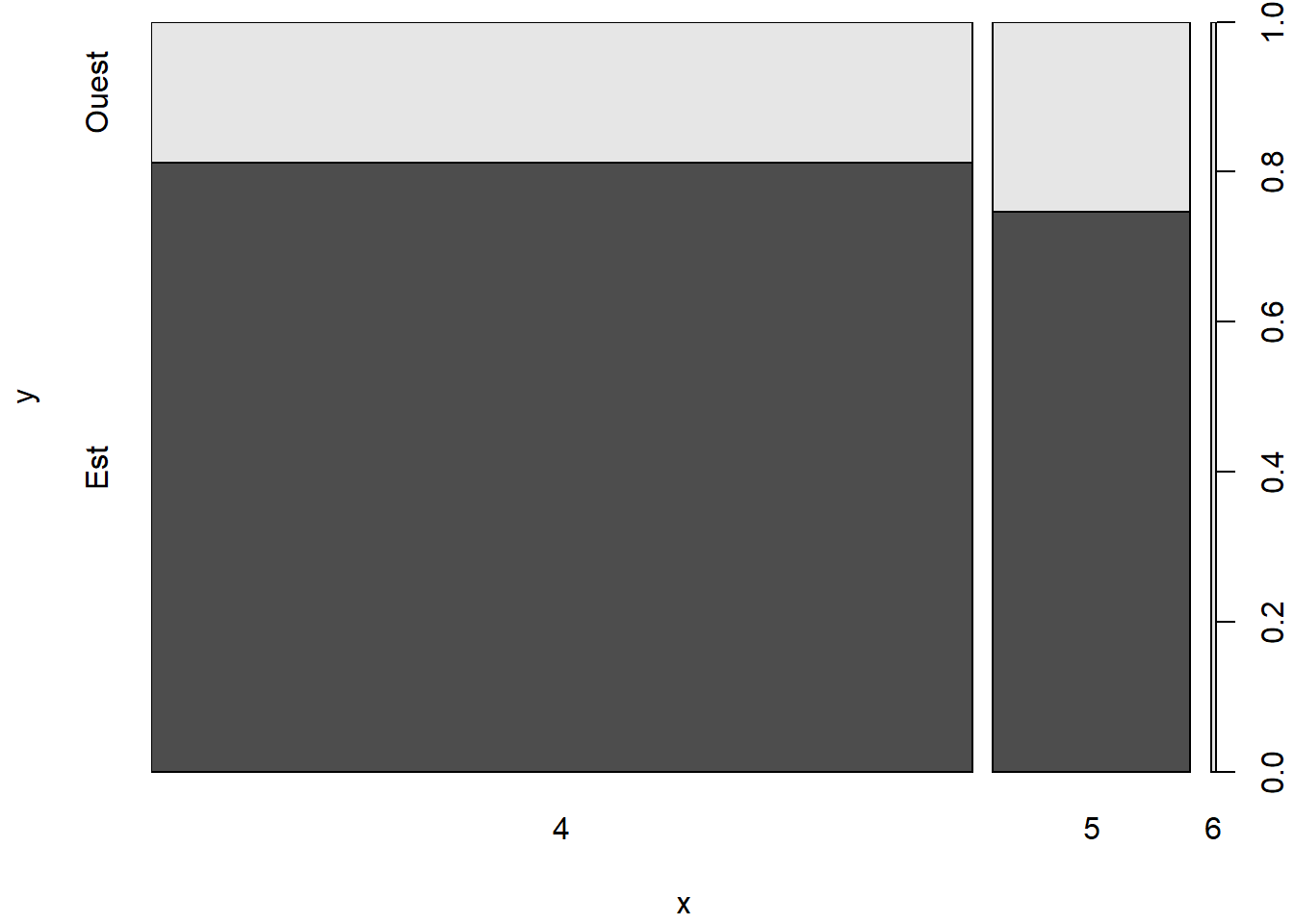
Si deux facteurs sont fournis en entrée, la méthode plot.factor choisit d’appeler la fonction spineplot. Elle produit un type particulier de diagramme en mosaïque, nommé en anglais spineplot.
Data frame à plus de 2 variables contenant des valeurs numériques ou transformables en valeurs numériques
# Utilisation du data frame quakes original, sans les deux facteurs ajoutés
plot(datasets::quakes)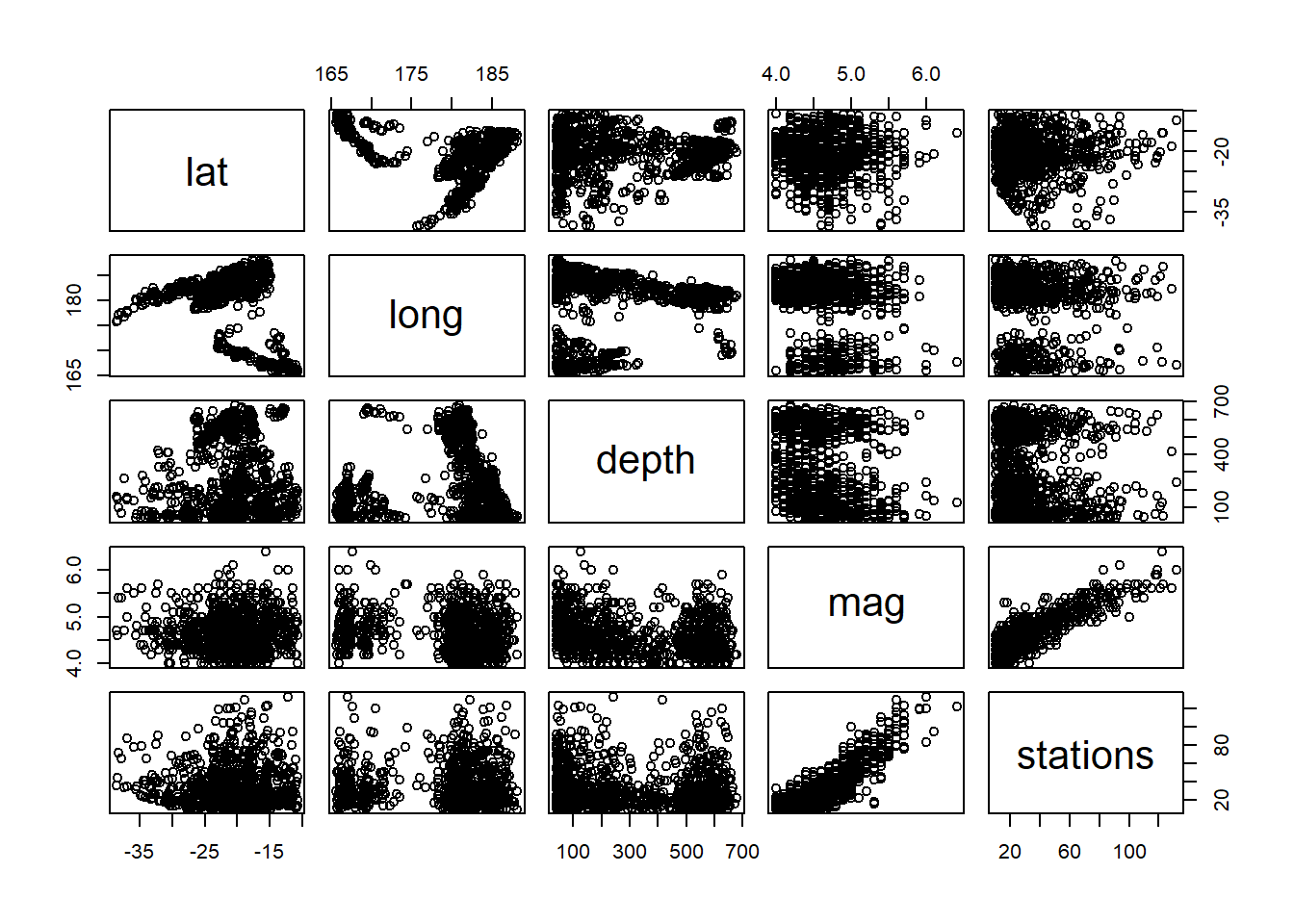
Si un data frame est fourni en entrée à la fonction générique plot, elle délègue son travail à la méthode plot.data.frame. Si ce data frame possède plus de 2 variables contenant des valeurs numériques (ou transformables en valeurs numériques), alors la méthode plot.data.frame choisit d’appeler la fonction pairs. Celle-ci produit une matrice de diagramme de dispersion.
Data frame à 2 variables
plot(quakes[, c("mag", "stations")])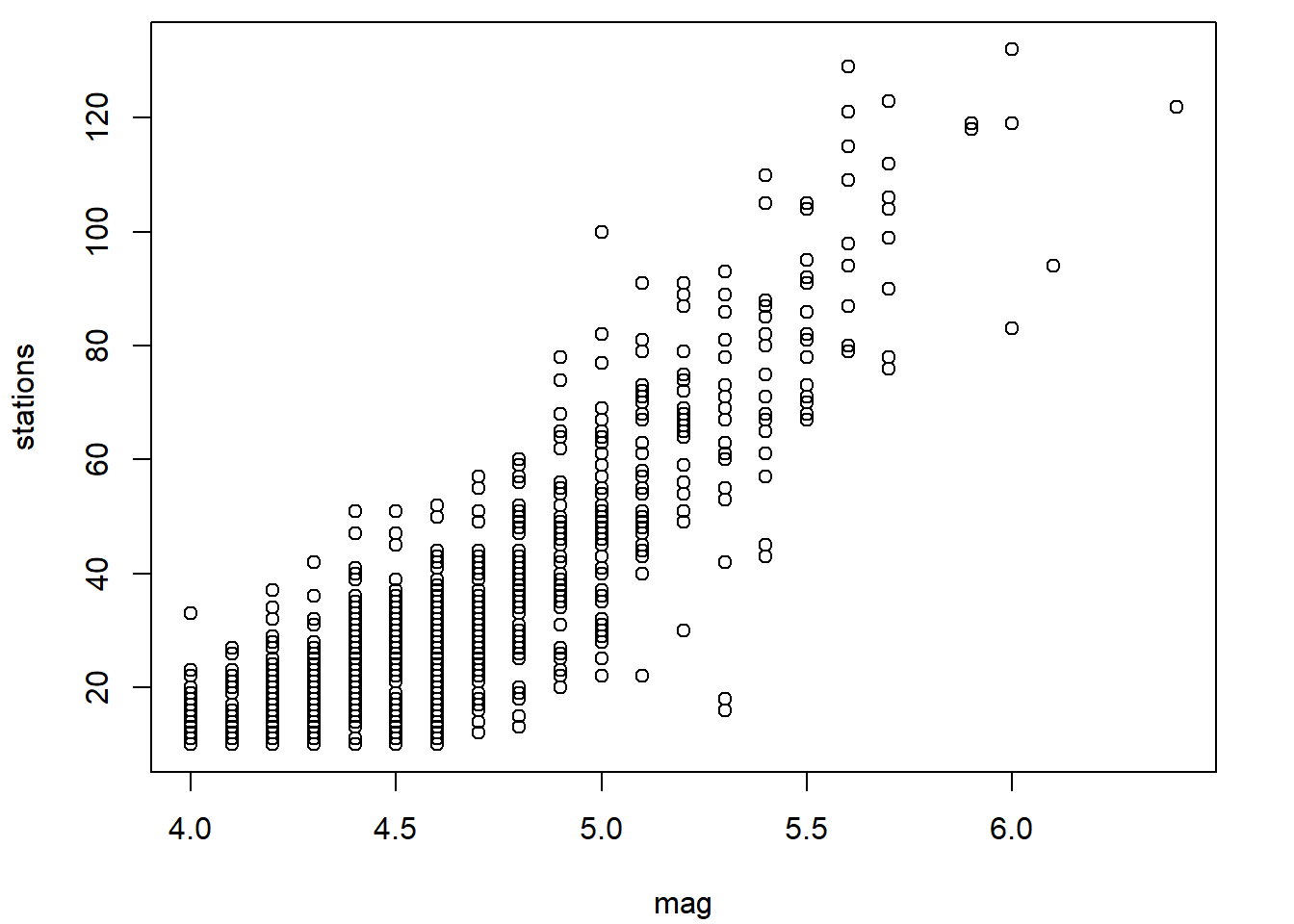
Si un data frame contenant seulement 2 variables est fourni en entré à plot, la méthode plot.data.frame évalue le type des données dans ces variables. Si les deux variables contiennent des valeurs numériques, la méthode plot.default est appelée pour produire un seul diagramme de dispersion. Les observations dans la première colonne sont placées sur l’axe des x et celle de la deuxième colonne sur l’axe des y.
plot(quakes[, c("mag_catego", "stations")])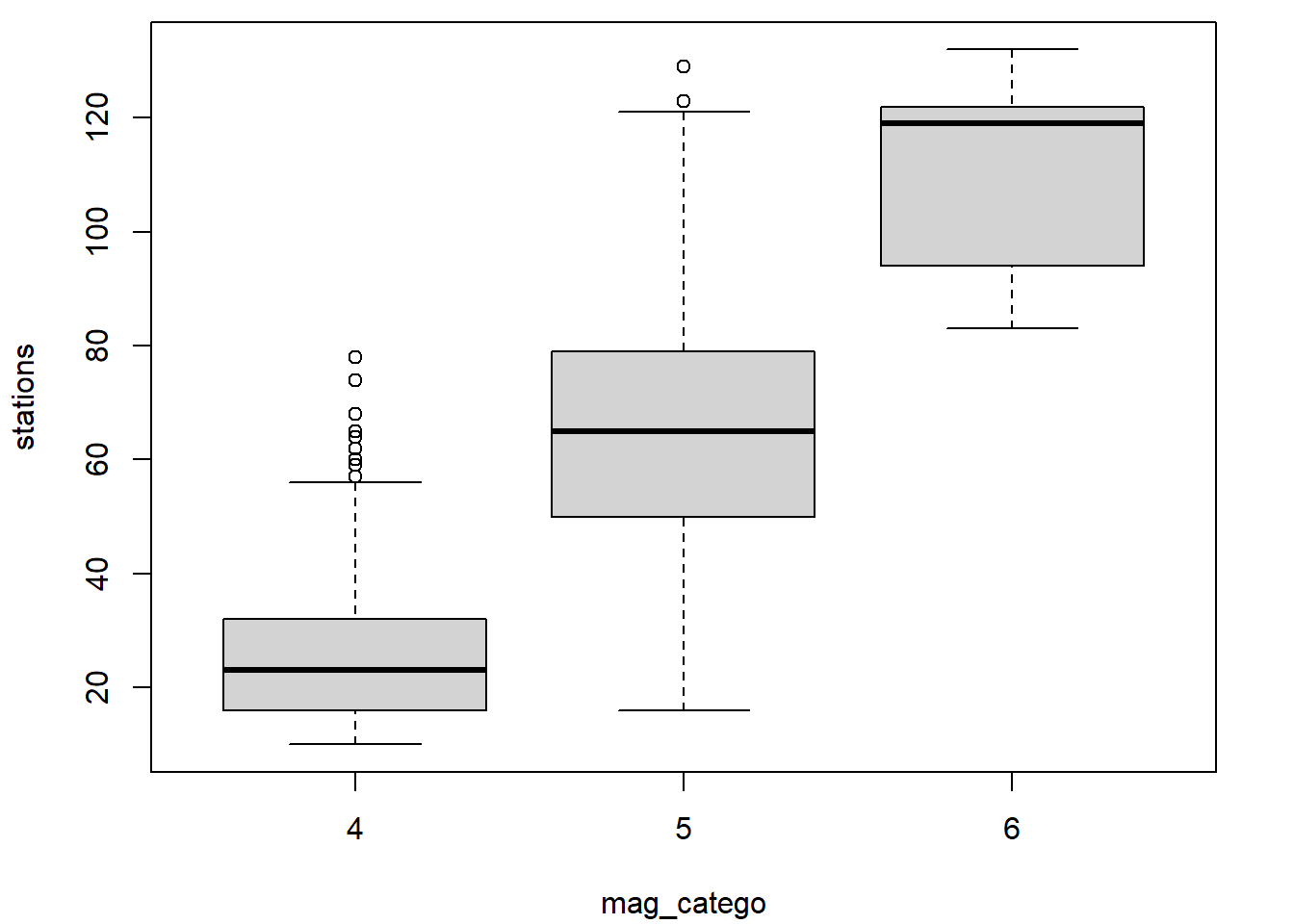
Si la première colonne est un facteur, des diagrammes en boîtes des observations dans la deuxième colonne, par niveaux du facteur dans le première colonne, sont produits avec la fonction boxplot.
plot(quakes[, c("mag_catego", "region")])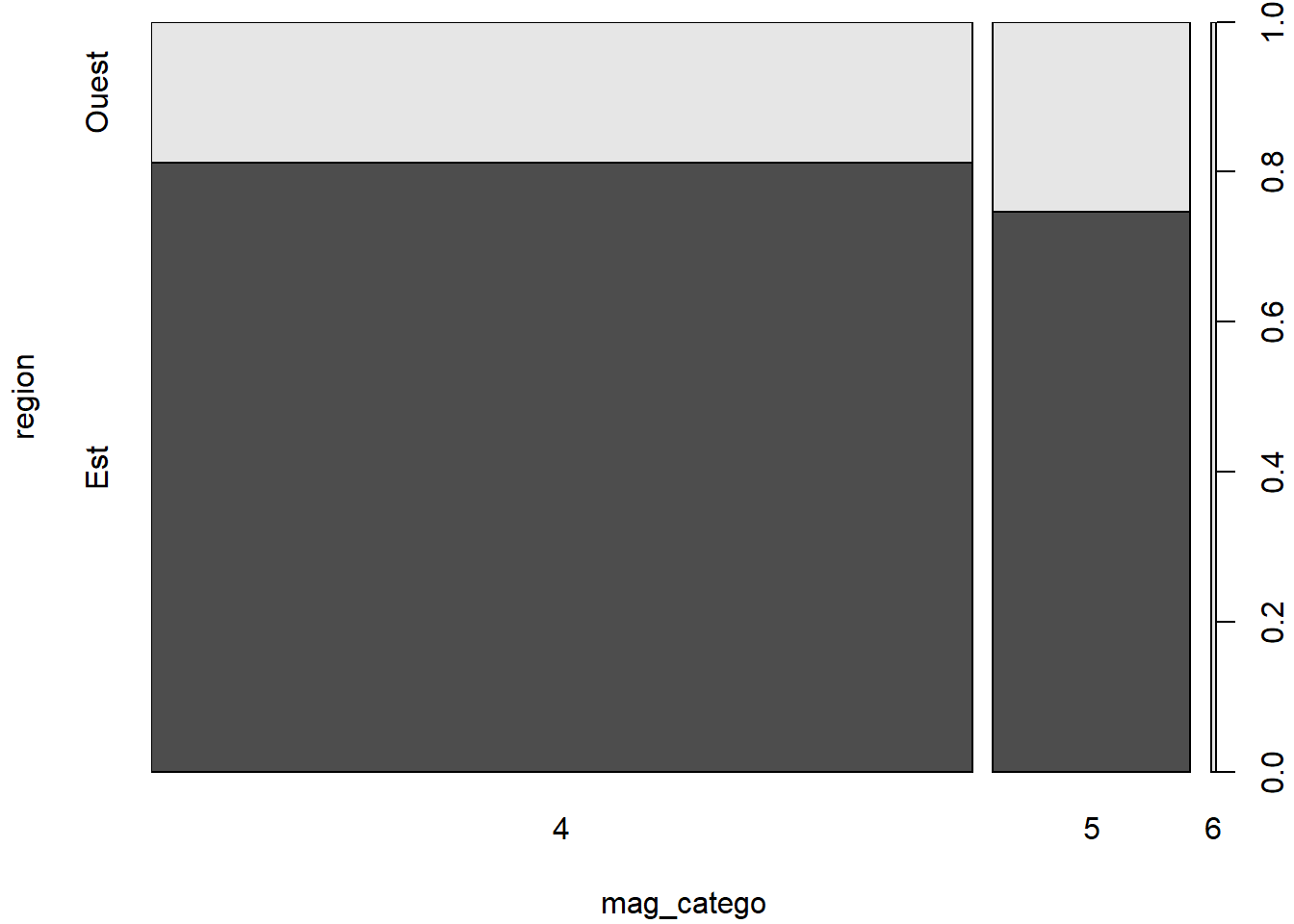
Si les deux variables sont des facteurs, plot.data.frame se comporte alors comme plot.factor lorsqu’il reçoit deux facteurs.
Data frame à une colonne
plot(quakes[, "mag", drop = FALSE])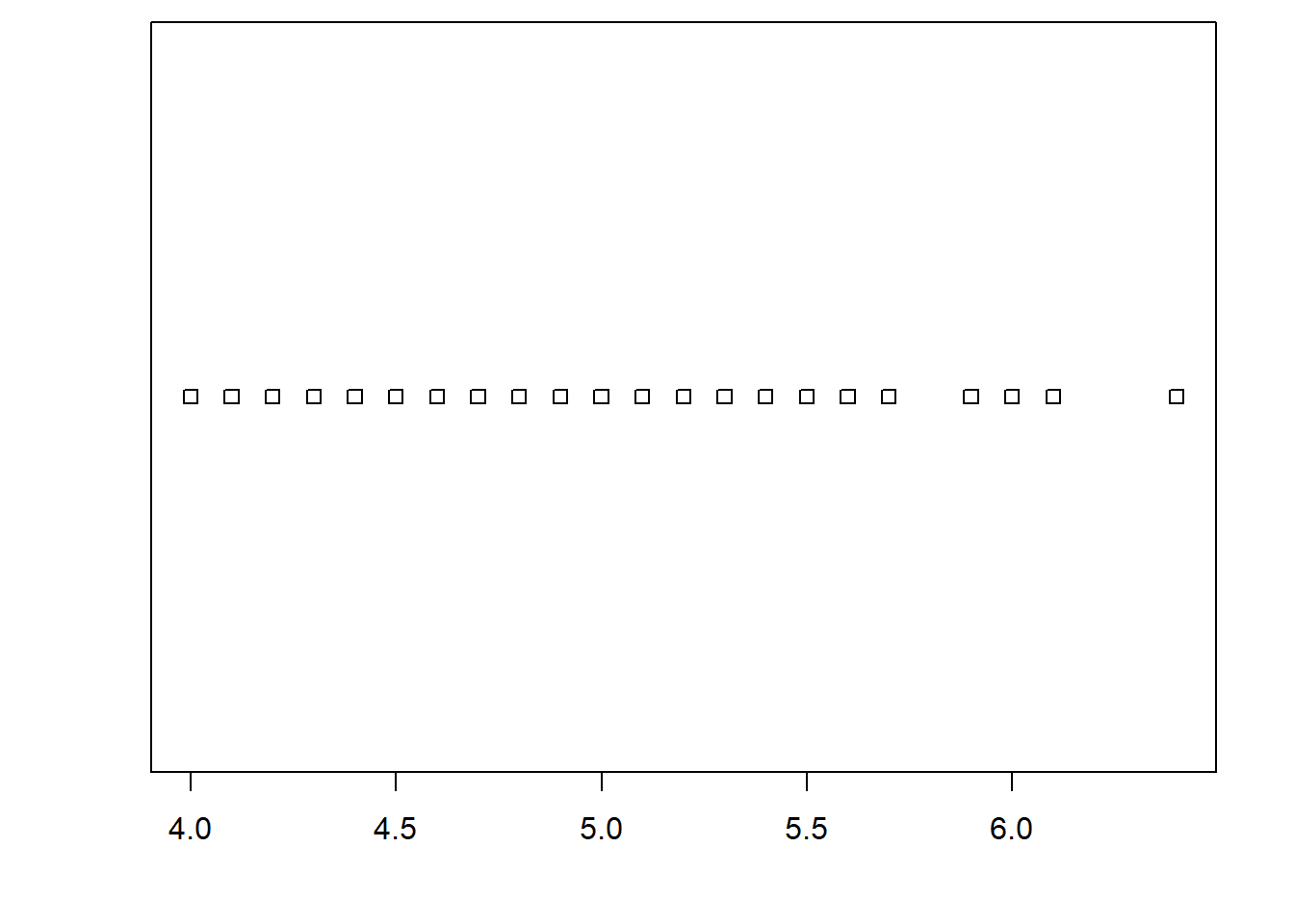
Si un data frame à seulement une colonne est fourni à plot et que cette colonne contient des observations numériques, un diagramme de dispersion à une dimension est produit, en appelant la fonction stripchart.
plot(quakes[, "mag_catego", drop = FALSE])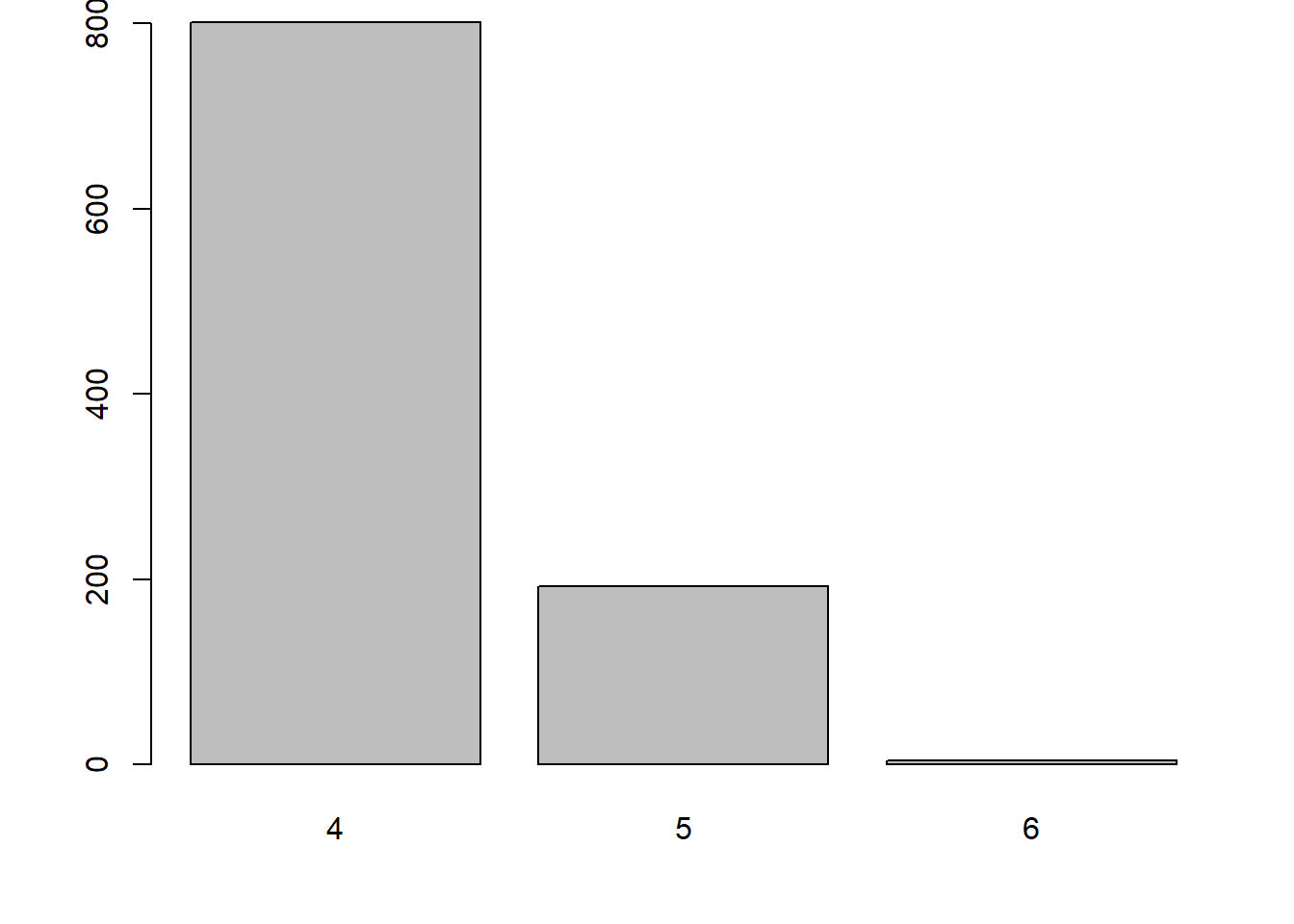
Si la colonne contient plutôt un facteur, c’est un diagramme à barres qui est produit par la fonction barplot.
Rappel : Sans l’argument drop = FALSE dans l’extraction d’une colonne de quakes, le résultat de l’extraction aurait été un vecteur ou un facteur (un objet à une dimension) plutôt qu’un data frame à une colonne.
str(quakes[, "mag_catego"])## Factor w/ 3 levels "4","5","6": 1 1 2 1 1 1 1 1 1 1 ...str(quakes[, "mag_catego", drop = FALSE])## 'data.frame': 1000 obs. of 1 variable:
## $ mag_catego: Factor w/ 3 levels "4","5","6": 1 1 2 1 1 1 1 1 1 1 ...Formule en entrée
La méthode plot accepte aussi une formule en entrée, auquel cas la méthode plot.formula est appelée. La méthode plot.formula est très versatile. La variable que nous lui fournissons dans la partie de gauche de la formule (à gauche de ~) est celle positionnée sur l’axe des y. La variable que nous lui fournissons dans la partie de droite de la formule est celle positionnée sur l’axe des x.
plot(stations ~ mag, data = quakes)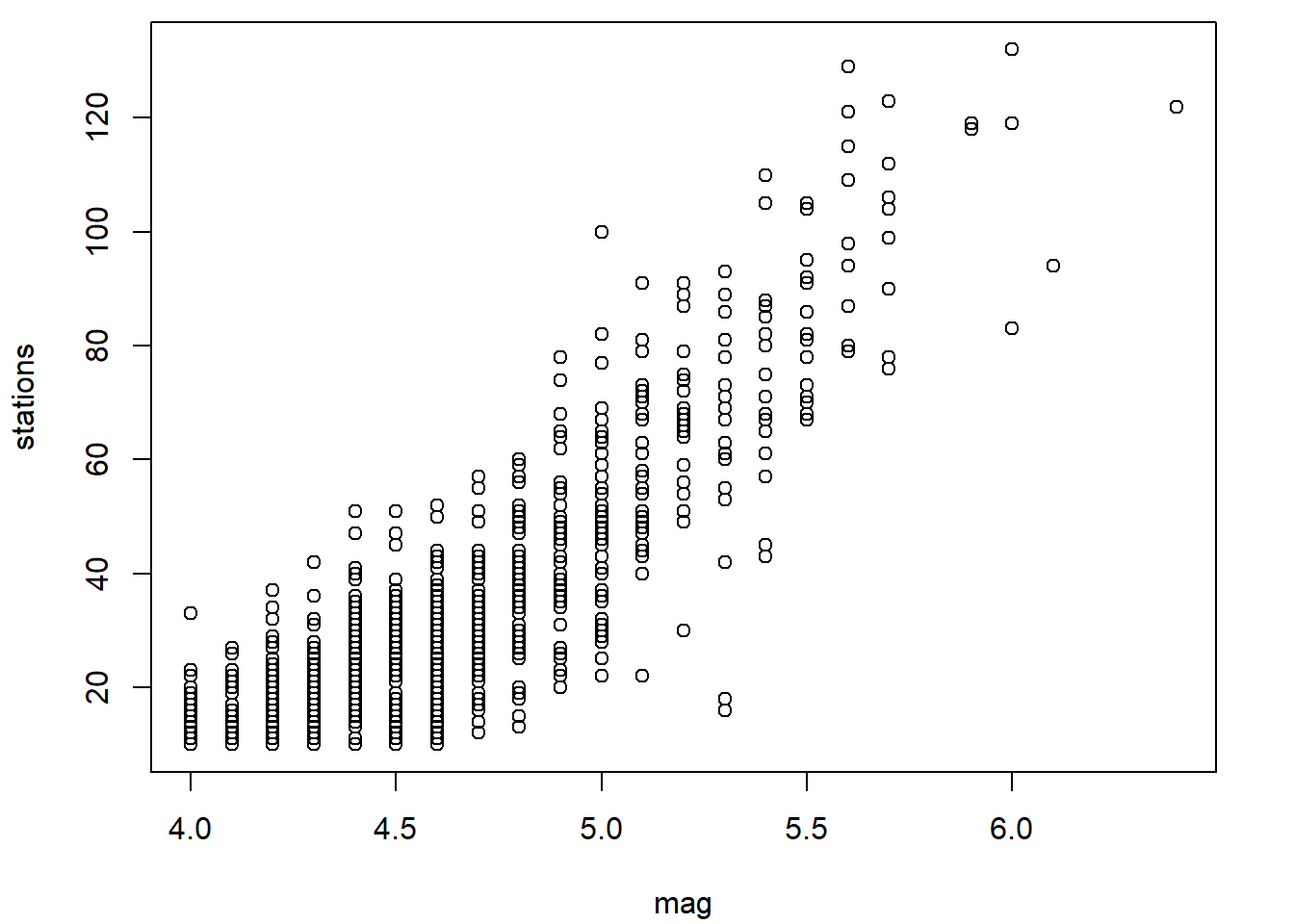
Si les deux variables sont numériques, un diagramme de dispersion est produit. Mais si la variable à droite est un facteur, des diagrammes en boîtes de la variable dans la partie de gauche de la formule, par niveau de ce facteur, sont produits.
plot(stations ~ mag_catego, data = quakes)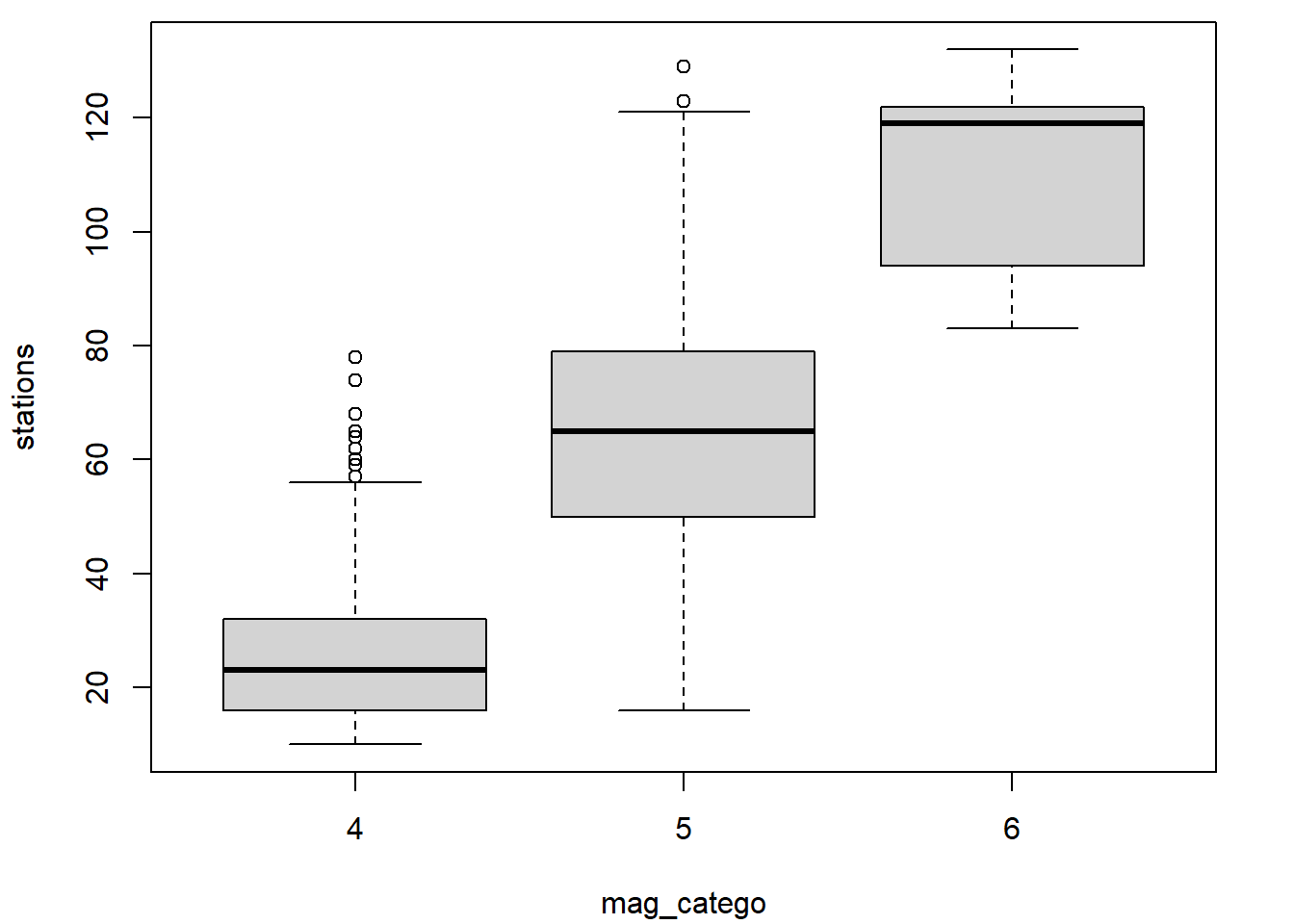
Si les deux variables sont des facteurs, un diagramme en mosaïque est produit.
plot(region ~ mag_catego, data = quakes)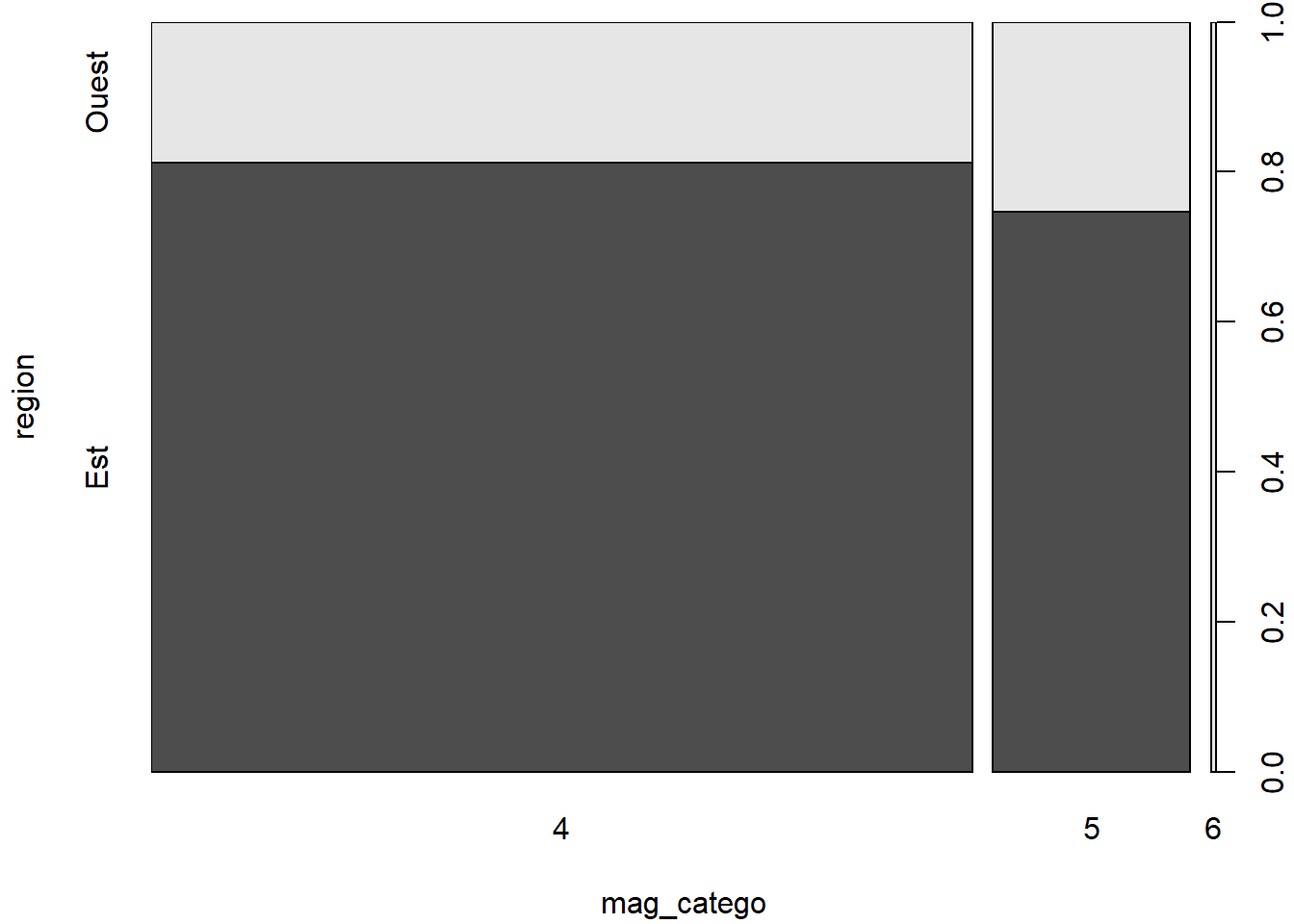
Nous pouvons aussi spécifier seulement une variable dans la formule. Par exemple, avec une seule variable dans la partie de droite de la formule (rien dans la partie de gauche de la formule), nous obtenons le même résultat qu’en fournissant un data frame à une colonne à la fonction générique plot.
plot(~ stations, data = quakes)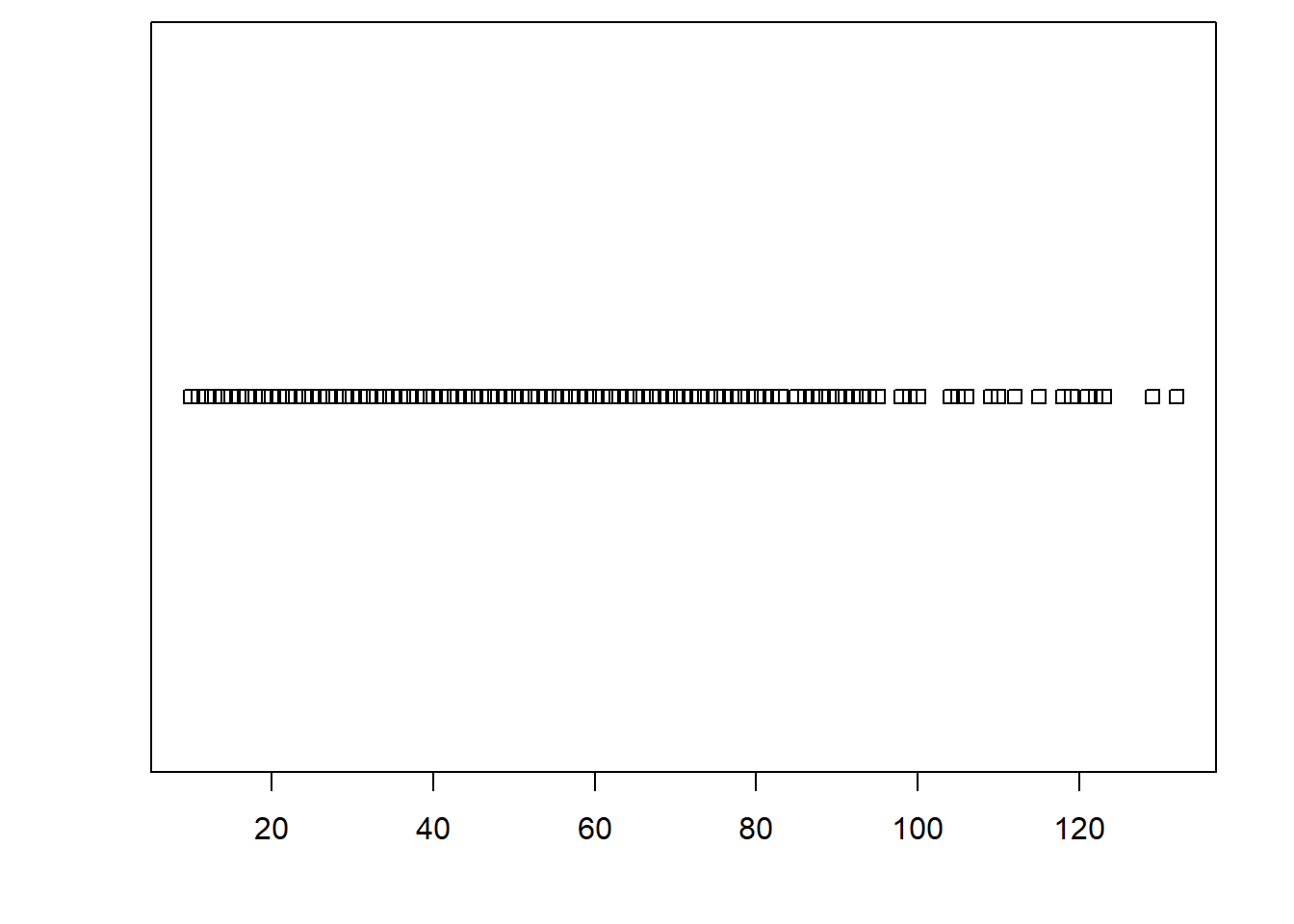
En plaçant plutôt l’unique variable dans la partie de gauche de la formule, avec la valeur 1 dans la partie de droite, nous obtenons le même résultat qu’en fournissant un seul vecteur ou facteur à la fonction générique plot.
plot(stations ~ 1, data = quakes)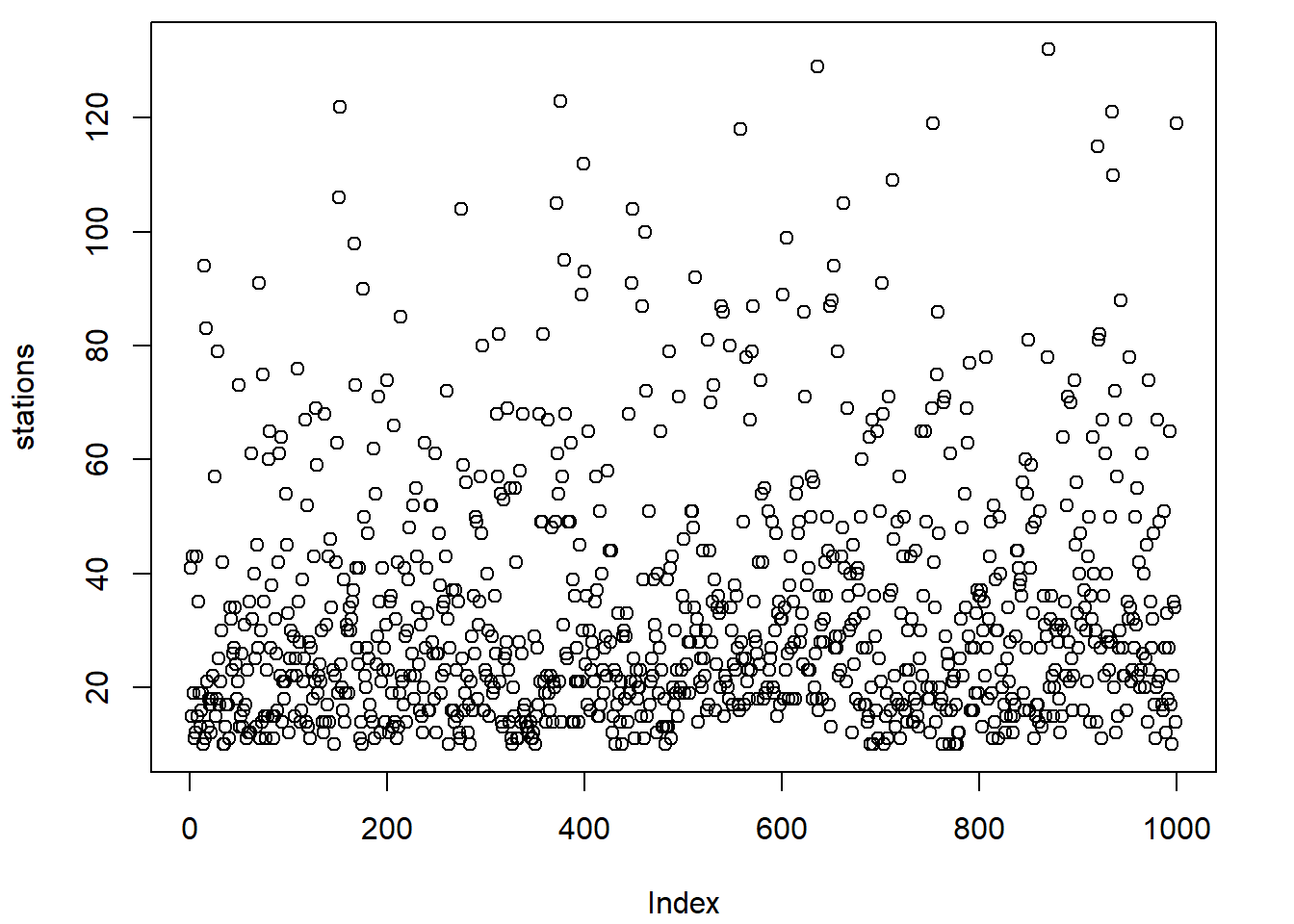
Si la formule contient une variable dans la partie de gauche et plus d’une variable dans la partie de droite, plus d’un graphique est produit.
plot(stations ~ mag + mag_catego, data = quakes)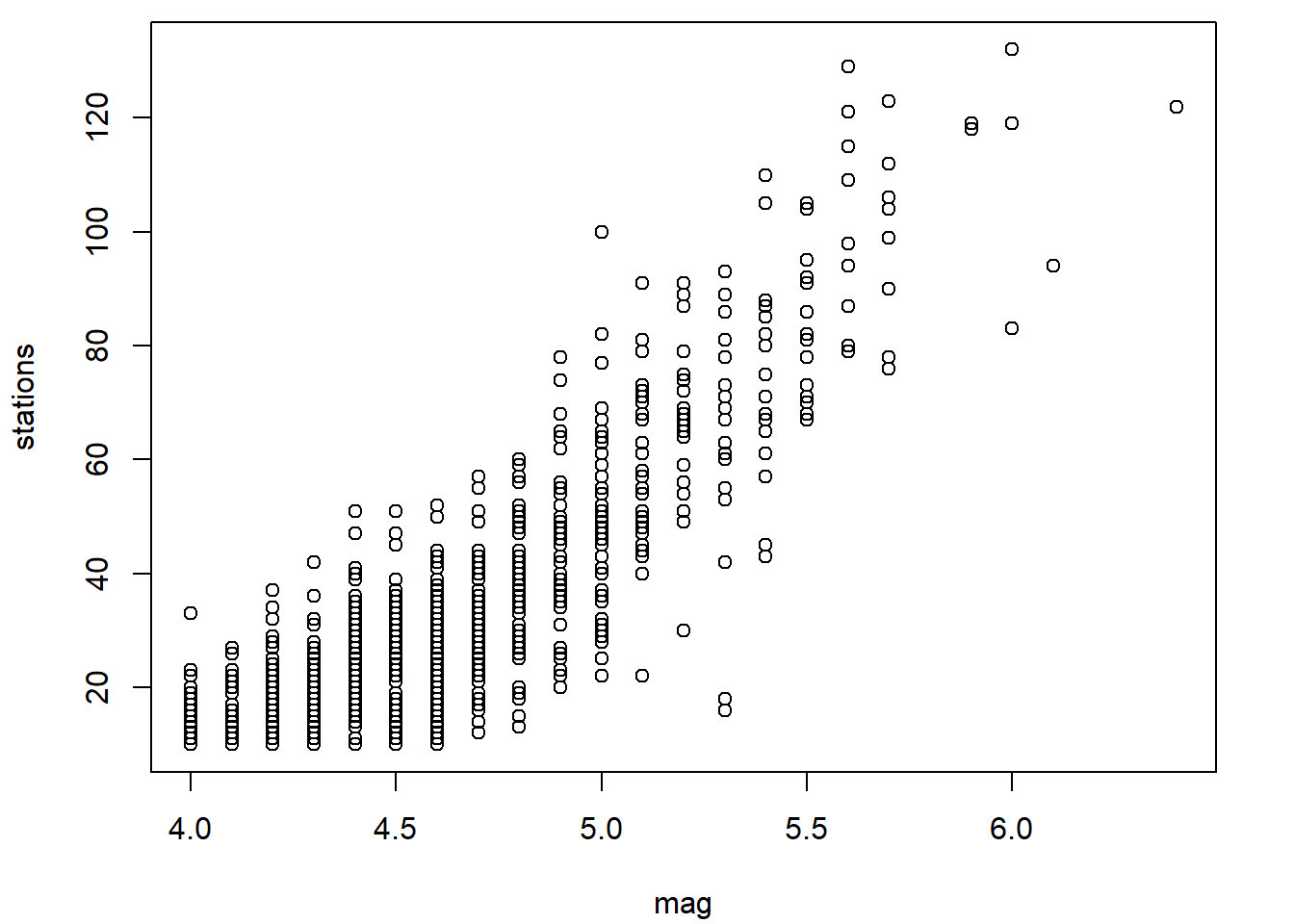
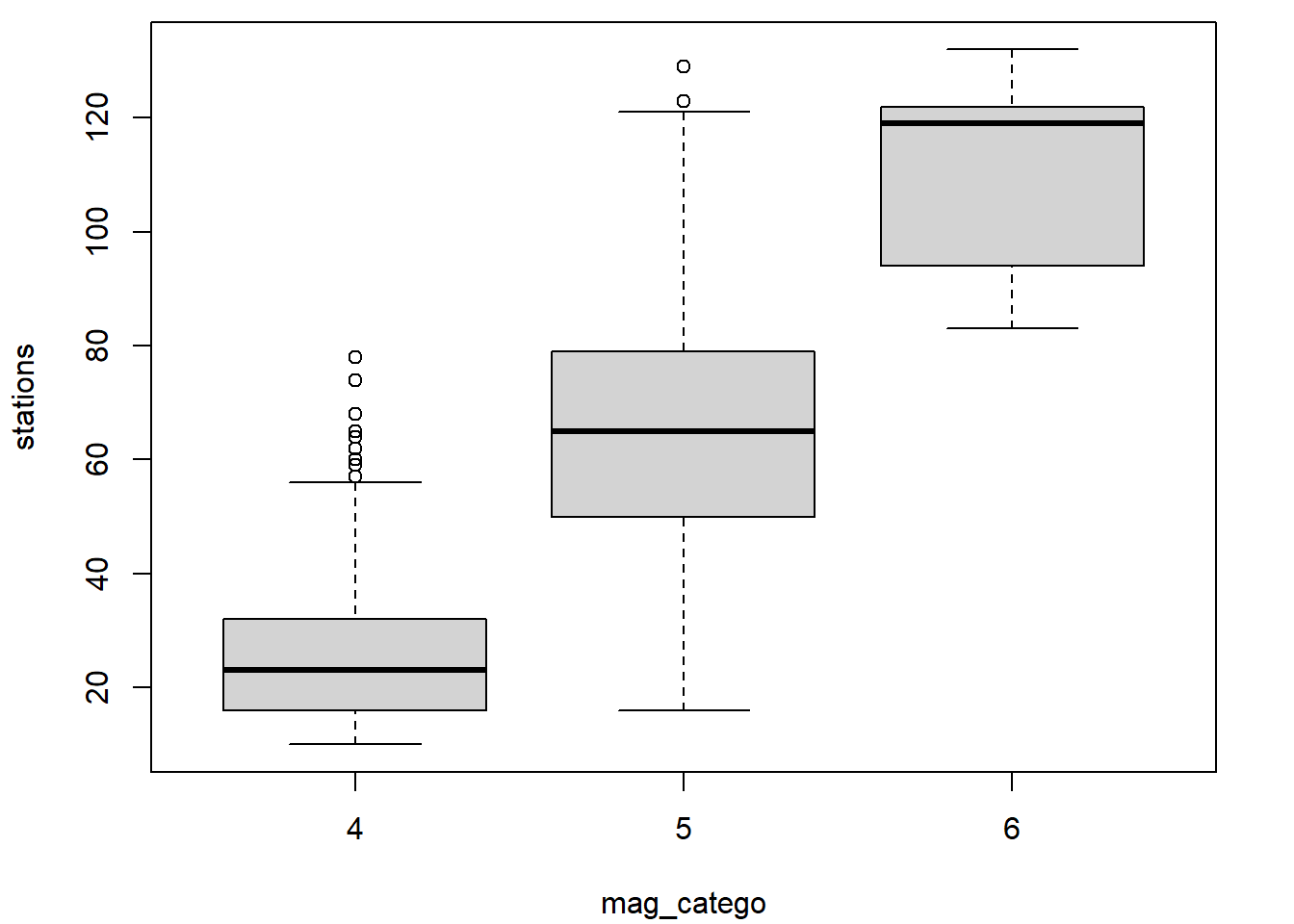
Mais si la formule ne contient pas de variable dans la partie de gauche et plus de deux variables dans la partie de droite, une matrice de diagrammes de dispersion est produite.
plot(~ lat + long + depth + mag + stations, data = quakes)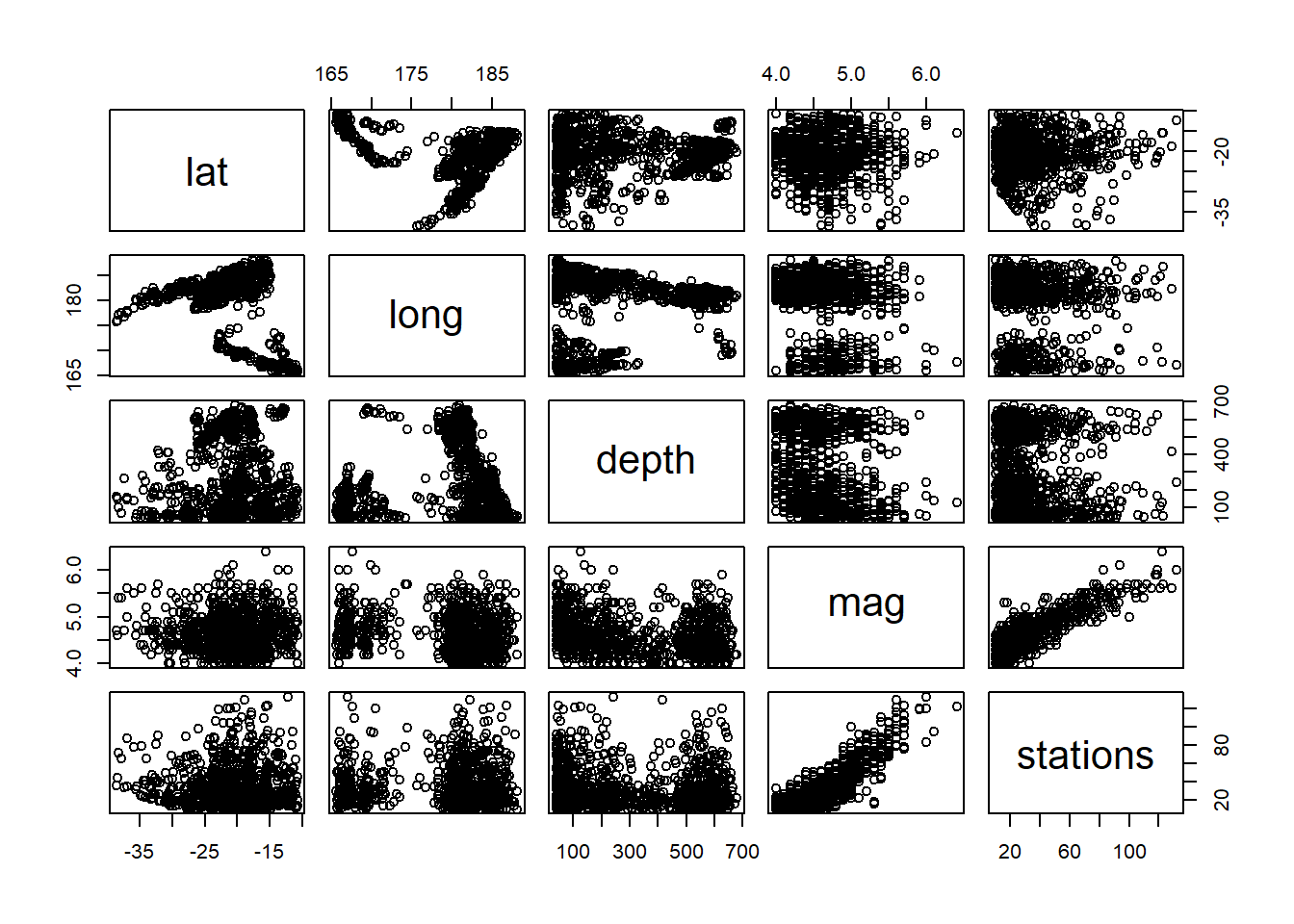
Bref, la méthode plot.formula fait appel à une des autres méthodes vues jusqu’à maintenant, en fonction de la position et de la nature (vecteur numérique ou facteur) des variables dans la formule.
Fonction en entrée
Il y a en R plusieurs fonctions prenant comme premier argument un vecteur numérique et retournant un vecteur de valeurs numériques, par exemple les fonctions R de type mathématique abs, srqt, exp, log, sin, cos, etc. Ce sont en quelque sorte des représentations de fonctions mathématiques d’une variable. La fonction générique plot peut tracer ces fonctions, grâce à sa méthode plot.function, après avoir évalué leurs valeurs en certains points.
plot(exp)
Par défaut, elle fait une évaluation de la valeur de la fonction en 101 points également répartis entre 0 et 1. Il est possible de modifier ces points grâce aux arguments from, to et n (une séquence de points est créée avec la fonction seq).
plot(exp, from = -4, to = 4, n = 501)
En fait, la méthode plot.function appelle la fonction curve.
par(all_par_default)