Calculs mathématiques en R

Sophie Baillargeon, Université Laval

2021-01-29

Version PDF de cette page web : calculs_math_r_2021.pdf

Note préliminaire : Lors de leur dernière mise à jour, ces notes ont été révisées en utilisant R version 4.0.3.

Dans un contexte d’analyse de données, il est courant de devoir effectuer un calcul mathématique simple, par exemple pour transformer une variable ou tester si des observations remplissent une certaine condition. Il est donc essentiel pour tout utilisateur de R de connaître les opérateurs et fonctions mathématiques de base, qui sont présentés ici.

De plus, il n’est pas rare qu’un programmeur R cherchant à implémenter une méthode de calcul doive utiliser de l’algèbre linéaire, du calcul différentiel et intégral ou encore de l’optimisation numérique. Ces possibilités de calculs mathématiques plus avancées en R sont aussi abordées ici (mais ces sujets ne seront pas évalués dans le cadre du cours STT-4230 / STT-6230 R pour scientifique).

1 Fonctionnement vectoriel et règle de recyclage

Tous les opérateurs et plusieurs des fonctions qui sont présentés dans cette fiche agissent de façon vectorielle. Ils effectuent un traitement élément par élément sur le ou les objets reçus en entrée.

Par exemple, si les deux matrices suivantes sont additionnées avec l’opérateur +,

matrix(1:6 , nrow = 2, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
matrix(6:1 , nrow = 2, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    6    4    2
## [2,]    5    3    1

l’élément en position (i,j) dans la première matrice sera additionné à l’élément à la même position dans la deuxième matrice, et ce, pour toutes les positions. Le résultat de cette addition terme à terme est donc le suivant :

matrix(1:6 , nrow = 2, ncol = 3) + matrix(6:1 , nrow = 2, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    7    7    7
## [2,]    7    7    7

Règle de recyclage

Si les deux objets intervenant dans l’opération ne sont pas de mêmes dimensions, la règle de recyclage s’applique. Cette règle avait déjà été mentionnée dans les notes sur les structures de données en R. Étant donné son importance, revoyons-là plus en profondeur ici.

x <- c(5, 6)
y <- c(2, 5, 3, 1)
x + y
## [1]  7 11  8  7

L’instruction précédente effectue 4 additions, une pour chacun des 4 éléments du plus long des deux vecteurs dans l’opération, soit ici le deuxième. Le premier vecteur est plutôt de longueur 2. R répète donc ses éléments pour créer un vecteur aussi long que le deuxième

rep(x, times = length(y)/length(x))
## [1] 5 6 5 6

et effectue en réalité l’opération suivante.

c(5, 6, 5, 6) + c(2, 5, 3, 1)
## [1]  7 11  8  7

Cette règle de recyclage est exploitée, souvent sans que l’utilisateur en soit pleinement conscient, lorsque l’un des deux vecteurs impliqués dans une opération est de longueur 1. Par exemple, la commande suivante impliquant un exposant,

y ^ 2
## [1]  4 25  9  1

est en fait traduite par R en la commande suivante :

y ^ rep(2, times = length(y))
## [1]  4 25  9  1

Règle de recyclage avec des objets à plus d’une dimension

La règle de recyclage s’applique aussi dans des opérations faisant intervenir des objets à plus d’une dimension. Par exemple, pour additionner le même vecteur, disons

y <- 3:1
y
## [1] 3 2 1

à chacune des colonnes d’une matrice, disons

mat <- matrix(1:12 , nrow = 3, ncol = 4)
mat
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

il suffit de lancer la commande suivante

mat + y
##      [,1] [,2] [,3] [,4]
## [1,]    4    7   10   13
## [2,]    4    7   10   13
## [3,]    4    7   10   13

au lieu de la suivante, qui retourne exactement le même résultat.

mat + matrix(rep(y, times = length(mat)/length(y)), nrow = nrow(mat), ncol = ncol(mat))

Dans cette dernière commande, les deux arguments fournis à l’opérateur + sont réellement de mêmes dimensions, car la deuxième matrice est la suivante

matrix(rep(y, length(mat)/length(y)), nrow = nrow(mat), ncol = ncol(mat))
##      [,1] [,2] [,3] [,4]
## [1,]    3    3    3    3
## [2,]    2    2    2    2
## [3,]    1    1    1    1

Une règle de recyclage utilisée pour former une matrice de dimension appropriée va donc remplir la matrice une colonne à la fois, comme le fait la fonction matrix par défaut.

Règle de recyclage lorsque la longueur de l’objet le plus long n’est pas multiple de la longueur de l’objet le plus court

Lorsque la longueur de l’objet le plus long n’est pas multiple de la longueur de l’objet le plus court, la règle de recyclage fonctionne quand même. R recycle l’objet le plus court assez de fois pour arriver à un objet de longueur égale ou supérieure à l’objet le plus long. Ensuite, si l’objet recyclé est plus long que l’autre objet, il est tronqué de façon à ce que les deux objets aient la même longueur.

Prenons par exemple les deux vecteurs suivants :

x <- 1:12
x
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12
y <- 5:1
y
## [1] 5 4 3 2 1

Supposons que la commande suivante soit soumise en R.

x + y

L’objet de gauche dans l’addition est de longueur 12 et l’objet de droite de longueur 5. L’objet de droite sera donc recyclé 3 fois,

y_recycle <- rep(5:1, times = ceiling(length(x)/length(y)))
y_recycle
##  [1] 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1

puis sa longueur sera réduite à la longueur de l’objet de gauche.

length(y_recycle) <- length(x)
y_recycle
##  [1] 5 4 3 2 1 5 4 3 2 1 5 4

Ensuite l’addition terme à terme sera effectuée.

x + y_recycle
##  [1]  6  6  6  6  6 11 11 11 11 11 16 16

Cependant, R émettra un avertissement pour nous informer qu’il a dû faire cet ajustement de longueur.

x + y
## Warning in x + y: longer object length is not a multiple of shorter object
## length
##  [1]  6  6  6  6  6 11 11 11 11 11 16 16

2 Fonctions et opérateurs mathématiques de base

2.1 Opérateurs mathématiques

2.1.1 Opérateurs arithmétiques

Voici une liste d’opérateurs arithmétiques disponibles en R :

  • + : addition,
  • - : soustraction,
  • * : multiplication,
  • / : division,
  • ^ : puissance,
  • %/% : division entière,
  • %% : modulo = reste de la division entière.

Les premiers opérateurs sont usuels et ne requièrent aucune explication. Expliquons cependant brièvement les deux derniers opérateurs de cette liste.

2.1.1.1 Division entière et modulo

L’opérateur %/% réalise une division entière. Pour illustrer ce type de division, prenons l’exemple suivant.

5 / 2
## [1] 2.5

L’opérateur de division ordinaire / retourne un nombre réel. L’opérateur %/% retourne la partie entière du résultat obtenu avec /. La partie décimale est tronquée.

5 %/% 2
## [1] 2

L’opérateur modulo %% retourne le reste de la division entière. Dans l’exemple traité ici, ce reste vaut 1 car 5 - 2*2 = 1.

5 %% 2
## [1] 1

Astuces :

  • Cet opérateur est pratique pour tester si des nombres sont pairs ou impairs. Les nombres pairs sont des multiples de 2. Alors x %% 2 retourne 0 pour les nombres pairs et 1 pour les nombres impairs.
  • L’opérateur modulo peut aussi servir à tester si un nombre stocké sous le type double est en réalité un entier au sens mathématique. S’il s’agit d’un entier, x %% 1 retournera 0.

2.1.2 Opérateurs de comparaison

Les opérateurs de comparaison permettent de comparer des valeurs. Ils retournent TRUE ou FALSE. Il s’agit des opérateurs suivants :

  • == : égalité,
  • != : non-égalité,
  • > : plus grand,
  • >= : plus grand ou égal,
  • < : plus petit,
  • <= : plus petit ou égal.

Supposons x et y les deux vecteurs numériques suivants.

x <- c(2, 5, 7, 3)
y <- c(3, 5, 6, 4)

Comparons ces vecteurs à l’aide d’un opérateur de comparaison. Est-ce que les valeurs contenues dans x sont supérieures aux valeurs contenues dans y ?

x > y
## [1] FALSE FALSE  TRUE FALSE

L’opérateur fonctionne de façon vectorielle, donc une comparaison est effectuée pour toutes les paires d’éléments à la même position dans les vecteurs x et y. Les valeurs dans le résultat retourné sont de type logique.

Les valeurs dans un vecteur peuvent aussi être comparées à une seule valeur, auquel cas la règle de recyclage s’applique.

x != 5
## [1]  TRUE FALSE  TRUE  TRUE

2.1.2.1 Comparaison de valeurs non numériques

Les opérateurs de comparaison ne fonctionnent pas seulement avec des valeurs numériques. Ils peuvent aussi être utilisés pour comparer des valeurs logiques ou caractères. Dans ce cas, il faut savoir que R considère que FALSE est inférieure à TRUE.

FALSE < TRUE 
## [1] TRUE

Quant aux caractères, les opérateurs de comparaison utilisent l’ordre de classement des caractères pour déterminer, entre deux valeurs, celle qui est inférieure. Cet ordre dépend des paramètres régionaux de la session R. D’une langue à l’autre, cet ordre peut varier.

Pour connaître l’ordre utilisé dans une session R, les instructions suivantes sont utiles :

caracteres_speciaux <- 
  c("!", "\"", "#", "$", "%", "&", "'", "(", ")", "*", "+", ",", "-", ".", "/", ":", ";", 
    "<", "=",">", "?", "@", "[", "\\", "]", "^", "_", "{", "|", "}", "~")
lettres_accentuees <- c("à", "â", "é", "è", "ê", "ë", "ï", "î", "ô", "ù", "ü", "û", "ç")
catacteres_ordonnes <- sort(c(caracteres_speciaux, 0:9, letters, LETTERS, 
                              lettres_accentuees, toupper(lettres_accentuees))) 
paste(catacteres_ordonnes, collapse = "")

J’ai obtenu le résultat suivant, qui sera peut-être différent sur votre ordinateur si vous n’avez pas les mêmes paramètres régionaux que moi.

"'-!\"#$%&()*,./:;?@[\\]^_{|}~+<=>0123456789aAàÀâÂbBcCçÇdDeEéÉèÈêÊëËfFgGhHiIîÎïÏjJkKlLmM
nNoOôÔpPqQrRsStTuUùÙûÛüÜvVwWxXyYzZ"

Ainsi, dans ma session R :

  • les caractères spéciaux sont inférieurs aux chiffres et aux lettres,
  • les chiffres sont inférieurs aux lettres,
  • les lettres sont classées en ordre alphabétique et
    • les lettres minuscules sont inférieures aux lettres majuscules,
    • les lettres non accentuées sont inférieures aux lettres accentuées.

Pour des chaînes à plus d’un caractère, la comparaison s’effectue caractère par caractère (premiers caractères comparés entre eux, puis deuxièmes en cas d’égalité, puis troisièmes en cas d’égalités aux deux premières positions, etc.).

"arborescence" < "arbre" 
## [1] TRUE

Aussi, l’absence de caractères vaut moins que la présence.

"a" < "aa"
## [1] TRUE

Remarque : Afin de correctement ordonner des nombres, il faut s’assurer de les stocker sous un format numérique. S’ils sont stockés sous forme de chaînes de caractères, les résultats obtenus ne seront pas toujours ceux attendus, comme dans cet exemple pour lequel 2 est dit non inférieur à 10 lorsque les nombres sont fournis à l’opérateur de comparaison sous forme de chaînes de caractères.

2 < 10
## [1] TRUE
"2" < "10"
## [1] FALSE

2.1.3 Opérateurs et fonction logiques vectoriels

Un opérateur ou une fonction logique vectoriel prend en entrée un ou deux vecteurs de logiques et retourne un autre vecteur de valeurs logiques. Le R de base comporte les opérateurs et la fonction logiques vectoriels suivants :

  • ! : négation,
  • & : et,
  • | : ou,
  • xor : ou exclusif.

2.1.3.1 Opérateur de négation !

L’opérateur ! n’a qu’un seul argument, alors que les autres opérateurs logiques en ont deux. Il effectue une négation, donc transforme les TRUE en FALSE et les FALSE en TRUE.

!c(TRUE, FALSE)
## [1] FALSE  TRUE

2.1.3.2 Opérateurs & et |, fonction xor

Les opérateurs & et |, ainsi que la fonction xor, appliquent de façon vectorielle les tables de vérité des fonctions mathématiques logiques « et », « ou » et « ou exclusif » respectivement.

Rappel : table de vérité de « et », « ou » et « ou exclusif »

p <- rep(c(FALSE, TRUE), each = 2)
q <- rep(c(FALSE, TRUE), times = 2)
cbind(p, q, "p et q" = p & q, "p ou q" = p | q, "p xor q" = xor(p, q))
##          p     q p et q p ou q p xor q
## [1,] FALSE FALSE  FALSE  FALSE   FALSE
## [2,] FALSE  TRUE  FALSE   TRUE    TRUE
## [3,]  TRUE FALSE  FALSE   TRUE    TRUE
## [4,]  TRUE  TRUE   TRUE   TRUE   FALSE

Ainsi,

  • l’expression p & q retournera un vecteur contenant des TRUE aux positions pour lesquelles la valeur en p et la valeur en q sont toutes les deux TRUE et contenant des FALSE partout ailleurs;
  • l’expression p | q retournera un vecteur contenant des FALSE aux positions pour lesquelles la valeur en p et la valeur en q sont toutes les deux FALSE et contenant des TRUE partout ailleurs;
  • l’expression xor(p, q) retournera un vecteur contenant des TRUE aux positions pour lesquelles la valeur en p ou la valeur en q est TRUE, mais pas les deux, et contenant des FALSE partout ailleurs.

2.1.4 Préséance des opérateurs

Dans une expression R contenant plusieurs opérateurs, mathématiques ou non, ceux-ci sont évalués dans un certain ordre, selon leur priorité d’opération. La fiche d’aide nommée Syntax (ouverte par la commande help(Syntax)) détaille l’ordre de préséance des différents opérateurs.

Pour les calculs mathématiques, les priorités d’opération usuelles sont respectées. Par exemple, dans l’expression 2 + 3 * 4, la multiplication est effectuée avant l’addition.

2 + 3 * 4
## [1] 14

Pour forcer l’évaluation d’un opérateur avant un autre de priorité plus élevée, il faut utiliser des parenthèses, comme dans cet exemple.

(2 + 3) * 4
## [1] 20

2.2 Fonctions mathématiques opérant de façon vectorielle

R offre aussi plusieurs fonctions de calculs mathématiques, travaillant de façon vectorielle, dont les suivantes :

Ces fonctions font un calcul distinct pour tous les éléments de l’objet fourni en entrée et retournent un résultat de même dimension que l’objet en entrée. Voici quelques exemples.

# Vecteur de données numériques pour les exemples
x <- seq(from = -1.25, to = 1.5, by = 0.25)
x
##  [1] -1.25 -1.00 -0.75 -0.50 -0.25  0.00  0.25  0.50  0.75  1.00  1.25  1.50
# Arrondissement régulier au dixième près
round(x, digits = 1)
##  [1] -1.2 -1.0 -0.8 -0.5 -0.2  0.0  0.2  0.5  0.8  1.0  1.2  1.5
# Arrondissement à l'entier supérieur
ceiling(x)
##  [1] -1 -1  0  0  0  0  1  1  1  1  2  2
# Arrondissement à la partie entière
trunc(x)
##  [1] -1 -1  0  0  0  0  0  0  0  1  1  1

Ces fonctions arrivent aussi à effectuer des calculs par élément dans un objet atomique de dimension supérieure à un ou dans un data frame.

# Matrice de données numériques pour les exemples
x_mat <- matrix(x, nrow = 2)
x_mat
##       [,1]  [,2]  [,3] [,4] [,5] [,6]
## [1,] -1.25 -0.75 -0.25 0.25 0.75 1.25
## [2,] -1.00 -0.50  0.00 0.50 1.00 1.50
# Extraction du signe
sign(x_mat)
##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]   -1   -1   -1    1    1    1
## [2,]   -1   -1    0    1    1    1

2.3 Fonctions mathématiques combinant des éléments

Certaines fonctions mathématiques en R effectuent des calculs faisant intervenir plus d’un élément de l’objet donné en entrée, plutôt que d’effectuer un calcul distinct pour chacun des éléments. C’est le cas des fonctions suivantes :

  • somme ou produit de tous les éléments (retourne une seule valeur) : sum, prod;
  • somme ou produit cumulatif des éléments (retourne un vecteur de même longueur que le vecteur en entrée) : cummsum, cumprod;
  • différences entre des éléments : diff.

Voici quelques exemples.

# Matrice de données numériques pour les exemples
mat <- matrix(c(2, 5, 3, 4, 6, 5, 4, 3, 1, 2, 9, 8), nrow = 3, ncol = 4)
mat
##      [,1] [,2] [,3] [,4]
## [1,]    2    4    4    2
## [2,]    5    6    3    9
## [3,]    3    5    1    8
# Produit de tous les éléments
prod(mat)
## [1] 6220800
# Somme cumulative des éléments (ici 2, 2+5, 2+5+3, 2+5+3+4, ...)
cumsum(mat)
##  [1]  2  7 10 14 20 25 29 32 33 35 44 52

Fonction diff

Pour une matrice ou un data frame, diff calcule les différences terme à terme des éléments composant les lignes. Par défaut, la fonction calcule pour chaque ligne, à l’exception de la première, la différence entre la ligne et la ligne au-dessus.

diff(mat)
##      [,1] [,2] [,3] [,4]
## [1,]    3    2   -1    7
## [2,]   -2   -1   -2   -1

La commande suivante retourne donc le même résultat que la précédente.

mat[-1, ] - mat[-nrow(mat), ]
##      [,1] [,2] [,3] [,4]
## [1,]    3    2   -1    7
## [2,]   -2   -1   -2   -1

Pour un vecteur, la fonction diff retourne les différences entre un élément (sauf le premier) et l’élément précédent.

diff(c(2, 5, 3, 4))
## [1]  3 -2  1

La fonction diff peut calculer des différences entre les éléments séparés par plus d’une position grâce à l’argument lag, comme dans cet exemple.

diff(c(2, 5, 3, 4), lag = 2)
## [1]  1 -1
# soustractions effectuées : 3-2 et 4-5

2.4 Opérations sur des ensembles

Les fonctions R d’opérations sur des ensembles sont les suivantes :

  • union : union,
  • intersect : intersection,
  • setdiff : différence,
  • setequal : test d’égalité,
  • is.element : test d’appartenance.

Les quatre premières fonctions permettent de comparer de différentes façons deux ensembles. Pour présenter des exemples d’utilisation des fonctions, créons donc d’abord deux ensembles fictifs. Ceux-ci sont stockés sous forme de vecteurs puisque le langage R de base n’offre pas de structure de données spécifique aux ensembles (contrairement au langage Python par exemple qui propose des sets).

A <- c("m", "s", "e", "f", "a")
B <- c("m", "e", "h", "i")

Rappelons que, par définition, un ensemble mathématique est une collection non ordonnée d’éléments uniques et, en conséquence, ne contient aucun élément dupliqué.

Union

La fonction union permet d’obtenir l’union des éléments de deux ensembles. Il s’agit d’un nouvel ensemble réunissant tous les éléments présents dans le premier ou le deuxième ensemble. Les éléments qui étaient présents dans les deux ensembles ne sont cependant pas en double dans l’union, car celle-ci est aussi un ensemble dont tous les éléments sont uniques.

union(A, B)
## [1] "m" "s" "e" "f" "a" "h" "i"

Pour arriver au même résultat sans utiliser une fonction d’opération sur des ensembles, nous aurions pu concaténer les vecteurs A et B,

c(A, B)
## [1] "m" "s" "e" "f" "a" "m" "e" "h" "i"

puis retirer les doublons du vecteur résultant avec la fonction unique (que nous reverrons dans les notes sur le prétraitement de données).

unique(c(A, B))
## [1] "m" "s" "e" "f" "a" "h" "i"

Intersection

La fonction intersect retourne l’intersection entre deux ensembles. Elle permet donc d’identifier les éléments communs à ces ensembles.

intersect(A, B)
## [1] "m" "e"

Différence

La fonction setdiff permet quant à elle d’identifier les éléments présents dans un premier ensemble sans être présents dans un second ensemble.

setdiff(A, B)
## [1] "s" "f" "a"

Contrairement aux fonctions union, intersect et setequal, l’ordre dans lequel les deux ensembles sont fournis en entrée à la fonction setdiff a un impact sur le résultat produit. L’exemple précédent a permis d’identifier les éléments appartenant à A sans appartenir à B, alors que la commande suivante retourne les éléments appartenant à B sans appartenir à A.

setdiff(B, A)
## [1] "h" "i"

Test d’égalité

La fonction setequal retourne toujours une seule valeur logique : TRUE si les deux ensembles fournis en entrée sont égaux, FALSE sinon.

setequal(A, B)
## [1] FALSE

Pour être égaux, deux ensembles doivent contenir les mêmes éléments, mais pas nécessairement dans le même ordre.

setequal(c(5, 3, 2), c(2, 3, 2, 5, 5))
## [1] TRUE

Notons que les fonctions union, intersect, setdiff et setequal ne vont pas rechigner si les ensembles qu’elles reçoivent en entrée contiennent des éléments dupliqués. Si c’est le cas, elles vont simplement retirer les doublons avant de procéder à l’opération.

Test d’appartenance

Finalement, R offre le fonction is.element pour tester la présence d’éléments dans un ensemble. Par exemple, la commande suivante test l’appartenance de "d" et "e" à l’ensemble A :

is.element(el = c("d", "e"), set = A)
## [1] FALSE  TRUE

La fonction retourne une valeur logique par élément testé, en respectant l’ordre dans lequel les éléments ont été identifiés via l’argument el. Ainsi, la sortie précédente indique que "d" n’est pas présent dans A, mais que "e" l’est.

2.5 Calcul de distances

Distance entre des variables numériques

Pour calculer des distances entre des observations numériques, la package stats offre la fonction dist. Voici un exemple d’utilisation de cette fonction traitant les célèbres données iris, incluses dans l’installation de base de R dans le data frame nommé iris (du package datasets). Prenons uniquement les 5 premières observations du jeu de données et conservons uniquement les variables numériques.

iris_ech_num <- iris[1:5, c("Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width")]
iris_ech_num
##   Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1          5.1         3.5          1.4         0.2
## 2          4.9         3.0          1.4         0.2
## 3          4.7         3.2          1.3         0.2
## 4          4.6         3.1          1.5         0.2
## 5          5.0         3.6          1.4         0.2

Calculons les distances euclidiennes entre toutes les paires d’observations dans ce jeu de données, basées sur les 4 variables numériques.

dist(x = iris_ech_num, method = "euclidean", diag = TRUE)
##           1         2         3         4         5
## 1 0.0000000                                        
## 2 0.5385165 0.0000000                              
## 3 0.5099020 0.3000000 0.0000000                    
## 4 0.6480741 0.3316625 0.2449490 0.0000000          
## 5 0.1414214 0.6082763 0.5099020 0.6480741 0.0000000

La distance euclidienne est un cas particulier de la distance de Minkowski, avec un paramètre \(p = 2\).

dist(x = iris_ech_num, method = "minkowski", p = 2, diag = TRUE)
##           1         2         3         4         5
## 1 0.0000000                                        
## 2 0.5385165 0.0000000                              
## 3 0.5099020 0.3000000 0.0000000                    
## 4 0.6480741 0.3316625 0.2449490 0.0000000          
## 5 0.1414214 0.6082763 0.5099020 0.6480741 0.0000000

La fonction dist propose quelques autres distances pour variables numériques (voir la fiche d’aide de la fonction pour la liste complète). Le package stats offre aussi la fonction mahalanobis pour calculer des distances de Mahalanobis.

Distance entre des chaînes de caractères

Pour faire le tour des fonctions de mesure de distances incluses dans l’installation R de base, mentionnons aussi la fonction adist du package utils qui calcule la distance de Levenshtein entre des chaînes de caractères, par exemple :

adist(x = "Allo", y = "Hello")
##      [,1]
## [1,]    2

La distance de Levenshtein, aussi appelée distance minimale d’édition, compte le nombre minimal d’insertions, de retraits et de substitutions à effectuer pour transformer la première chaîne de caractères en la deuxième. Il est possible d’associer un coût différent à chacune de ces opérations. Par défaut, elles ont toutes un coût de 1. La distance de Levenshtein entre "Allo" et "Hello" vaut 2 parce que pour transformer "Allo" en "Hello" il faut au minimum faire les deux opérations suivantes :

  • ajouter une lettre (par exemple un H au début);
  • transformer une lettre (par exemple transformer le "A" en "e").

2.6 Constantes mathématiques

En R, le nombre \(\pi\) est représenté par la constante pi.

pi
## [1] 3.141593

Inf est la constante R pour l’infini \(\infty\).

-5 / 0
## [1] -Inf

NaN est une constante signifiant Not A Number. Cette constante est retournée par R lorsqu’un utilisateur lui demande d’effectuer une opération mathématique impossible, par exemple :

log(-1)
## Warning in log(-1): NaNs produced
## [1] NaN

Rappel : Attention à ne pas confondre la constante NaN avec la constante NA qui signifie plutôt Not Available et qui sert à représenter les données manquantes.

3 Conditions logiques

Une condition logique est simplement une expression R qui retourne une ou des valeurs logiques (TRUE ou FALSE). Ce type d’expression a différentes utilités, par exemple :

  • explorer des données : répondre à des questions du genre combien d’observations respectent une certaine condition;
  • filtrer des données : extraire les observations respectant une certaine condition;
  • définir une condition dans une structure de contrôle conditionnelle if ... else;
  • etc.

3.1 Conditions logiques vectorielles

Les deux premières utilités potentielles des conditions logiques énumérées ci-dessus requièrent la création d’un vecteur de valeurs logiques de la même longueur que l’objet R sur lequel la condition est testée. Nous avons vu au début de cette fiche des outils pour écrire de telles conditions logiques :

Voici des exemples d’écriture de conditions logiques utilisant le vecteur suivant, que nous avons déjà manipulé dans des notes précédentes.

de <- c(2, 3, 4, 1, 2, 3, 5, 6, 5, 4)

Supposons que nous voulions connaître le nombre d’éléments dans ce vecteur numérique dont la valeur est supérieure à 3. La condition logique suivante nous permet d’identifier ces valeurs.

condition <- de > 3
condition
##  [1] FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE

Compter le nombre de valeurs supérieures à 3 dans de revient à compter le nombre de TRUE dans le vecteur précédent. Ce calcul se réalise facilement avec la fonction sum comme suit.

sum(condition)
## [1] 5

Même si une somme est une opération mathématique sur des valeurs numériques, la commande précédente ne retourne par d’erreur, car R réalise d’abord une conversion implicite de type de données pour transformer les valeurs logiques en nombres (TRUE devient 1 et FALSE devient 0), puis effectue la somme.

3.1.1 Extraction d’éléments selon une condition logique

Le vecteur condition serait aussi utile pour extraire les éléments de de ayant une valeur supérieure à 3. Nous savons que l’opérateur d’indiçage [ et la fonction d’extraction subset acceptent en entrée un vecteur logique. Nous pouvons donc extraire les éléments respectant la condition comme suit.

de[condition]
## [1] 4 5 6 5 4

3.1.1.1 Fonction which

La fonction which permet de connaître les positions des TRUE dans le vecteur, comme l’illustre cet exemple :

which(condition)
## [1]  3  7  8  9 10

L’utilisation de which n’est cependant pas nécessaire lors de l’extraction d’éléments à partir d’un vecteur logique. Par exemple, les commandes de[which(condition)] et de[condition] produisent le même résultat, mais la commande sans appel à la fonction which a l’avantage d’être plus succincte.

3.1.1.2 Conditions combinant des vecteurs logiques

La condition précédente était plutôt simple. Une condition plus complexe requiert souvent de combiner des vecteurs logiques à l’aide d’un opérateur logique. Par exemple, l’instruction suivante identifie les éléments du vecteur de dont la valeur se situe dans l’intervalle \([3, 5]\).

de >= 3 & de <= 5
##  [1] FALSE  TRUE  TRUE FALSE FALSE  TRUE  TRUE FALSE  TRUE  TRUE

L’instruction suivante identifie pour sa part les éléments du vecteur de égaux à 1, 4 ou 6.

de == 1 | de == 4 | de == 6
##  [1] FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE

Pour identifier les éléments du vecteur de non-égaux à 1, 4 ou 6, nous pourrions inverser le vecteur logique précédent avec l’opérateur de négation comme suit.

!(de == 1 | de == 4 | de == 6)
##  [1]  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE

Rappelons qu’en logique mathématique, la négation d’une disjonction est équivalente à la conjonction de négations. L’instruction suivante retourne donc le même résultat que la précédente.

de != 1 & de != 4 & de != 6
##  [1]  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE

3.1.2 Opérateur %in% de comparaison à plusieurs valeurs

Pour effectuer une comparaison à un ensemble de valeur, telle que le fait l’instruction de == 1 | de == 4 | de == 6, R offre un opérateur raccourcissant la syntaxe : l’opérateur %in%. Cet opérateur compare les éléments d’un vecteur (placé avant l’opérateur) aux éléments d’un ensemble présenté sous la forme d’un vecteur (placé après). Il retourne TRUE pour un élément égal à n’importe lequel des éléments de l’ensemble, FALSE sinon. L’instruction de == 1 | de == 4 | de == 6 est donc équivalent à la suivante.

de %in% c(1, 4, 6)
##  [1] FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE

Combiné à un opérateur de négation !, l’opérateur %in% permet de facilement tester si les valeurs dans un vecteur sont différentes des valeurs d’un ensemble, comme dans cet exemple.

! de %in% c(1, 4, 6)
##  [1]  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE

3.1.3 Fonctions de comparaison pour constantes spéciales

Notons que tester si un ou des éléments sont égaux à NA, NaN, Inf ou -Inf, ne se fait pas directement avec l’opérateur == comme suit.

c(1, 2, NA, 4, 5) == NA
## [1] NA NA NA NA NA

Il faut plutôt utiliser la fonction is.na, is.nan ou is.infinite.

is.na(c(1, 2, NA, 4, 5))
## [1] FALSE FALSE  TRUE FALSE FALSE

La fonction is.finite retourne pour sa part TRUE pour les éléments non égaux à NA, NaN, Inf ou -Inf.

is.finite(c(NA, NaN, Inf, -Inf, 4.5, 3))
## [1] FALSE FALSE FALSE FALSE  TRUE  TRUE

3.2 Conditions logiques de longueur 1

Lors de l’écriture d’une condition logique, il faut parfois s’assurer de retourner un vecteur logique de longueur 1. C’est le cas lors de l’écriture d’une condition logique dans une structure de contrôle conditionnelle if ... else (que nous verrons plus loin). La condition dans un if doit être obligatoirement de longueur 1.

3.2.1 Opérateurs et fonctions logiques non vectoriels

Les opérateurs et fonctions logiques suivants garantissent que le résultat retourné est de longueur 1.

  • && : et,
  • || : ou,
  • isTRUE et isFALSE.

Les opérateurs && et || appliquent les mêmes tables de vérité que les opérateurs & et |, mais ils ne travaillent pas de façon vectorielle. Si, par inadvertance, && ou || reçoit en entrée des vecteurs de longueurs supérieures à 1, il effectue une opération seulement sur les premiers éléments de ces vecteurs, comme dans cet exemple.

de == 1 || de == 4 || de == 6
## [1] FALSE

Les fonctions isTRUE et isFALSE, pour leur part, sont des fonctions raccourcies permettant d’effectuer les tests suivants.

is.logical(x) && length(x) == 1 && !is.na(x) && x   # isTRUE
is.logical(x) && length(x) == 1 && !is.na(x) && !x  # isFALSE

Elles permettent donc de s’assurer qu’une condition possède toutes les caractéristiques requises pour être fournie à un if (contenir des données logiques, être de longueur 1 et ne pas prendre la valeur NA).

3.2.2 Fonctions all et any

Les fonctions all et any font partie des fonctions R retournant toujours une seule valeur logique. La fonction all indique si tous les éléments d’un vecteur logique sont TRUE. Par exemple, pour tester si toutes les valeurs dans le vecteur de sont entières au sens mathématique, nous pourrions utiliser la commande suivante.

all(de %% 1 == 0)
## [1] TRUE

La fonction any indique pour sa part si au moins un élément d’un vecteur logique est TRUE. Nous pourrions par exemple vérifier si le vecteur de comporte des valeurs négatives comme suit.

any(de < 0)
## [1] FALSE

3.2.3 Fonctions de vérification de type

Finalement, les fonctions is.numeric, is.character, is.logical, is.vector, is.matrix, is.data.frame, is.factor, is.null, is.function, etc., testent une condition et retournent toujours un logique de longueur unitaire. Par exemple, testons si le vecteur de contient bien des données numériques.

is.numeric(de)
## [1] TRUE

4 Comparaison de deux objets R

Les opérateurs de comparaison vus ci-dessus permettent de comparer les éléments d’objets R. Mais comment comparer des objets entiers? Cela dépend de ce qui doit être comparé.

  • Pour comparer toutes les données contenues dans deux objets atomiques, mais pas les métadonnées (attributs) : all(x == y)
    • retourne TRUE si toutes les données sont égales,
    • FALSE sinon,
    • NA si un des deux objets comparés contient au moins une donnée manquante et que l’argument na.rm de la fonction all prend la valeur FALSE,
    • la règle de recyclage s’applique si les objets ne sont pas de mêmes dimensions.
  • Pour comparer deux objets dans leur totalité (éléments, attributs, type de l’objet et de ses éléments) : identical(x, y)
    • retourne TRUE si les deux objets comparés sont totalement identiques,
    • FALSE sinon.
  • Pour comparer tous les éléments et les attributs de deux objets, en acceptant des différences dans les données numériques selon une certaine tolérance : all.equal(x, y)
    • retourne TRUE en cas d’égalité respectant la tolérance,
    • sinon retourne des informations sur les différences.

Voici quelques exemples.

Données identiques, mais métadonnées différentes

# Objets comparés
x <- 1:5
y <- 1:5
names(x) <- letters[1:5]
str(x)
##  Named int [1:5] 1 2 3 4 5
##  - attr(*, "names")= chr [1:5] "a" "b" "c" "d" ...
str(y)
##  int [1:5] 1 2 3 4 5

 

# Résultats des différentes comparaisons
all(x == y)
## [1] TRUE
identical(x, y)
## [1] FALSE
all.equal(x, y)
## [1] "names for target but not for current"

Données équivalentes, mais de types différents, métadonnées identiques

# Objets comparés
x <- as.double(x)
str(x)
##  num [1:5] 1 2 3 4 5
str(y)
##  int [1:5] 1 2 3 4 5

 

# Résultats des différentes comparaisons
all(x == y)
## [1] TRUE
identical(x, y)
## [1] FALSE
all.equal(x, y)
## [1] TRUE

Données numériques pas tout à fait identiques, métadonnées et types identiques

# Objets comparés
y <- 1:5 + 1e-10
str(x)
##  num [1:5] 1 2 3 4 5
str(y)
##  num [1:5] 1 2 3 4 5

Bien que les données numériques dans x et y ne soient pas tout à fait identiques, elles semblent identiques à l’affichage de x et y.

# Résultats des différentes comparaisons
all(x == y)
## [1] FALSE
identical(x, y)
## [1] FALSE
all.equal(x, y)
## [1] TRUE

Rappel : Il est possible de contrôler le nombre de chiffres composant un nombre affiché dans la console R avec l’option digits de la session R.

optionsDefaut <- options()
options(digits = 11)
y
## [1] 1.0000000001 2.0000000001 3.0000000001 4.0000000001 5.0000000001
options(digits = optionsDefaut$digits)

5 Calculs plus avancés

Voici des informations concernant trois sujets mathématiques plus poussés. Cette matière ne sera pas évaluée dans le cadre du cours, car certains étudiants n’ont pas les connaissances préalables pour facilement la comprendre. Il est cependant fort probable que certaines des informations présentées ci-dessous soient un jour utiles aux étudiants gradués en statistique. L’implémentation de méthodes statistiques fait souvent intervenir ces types de calculs.

5.1 Algèbre linéaire

Il existe plusieurs fonctions en R pour faire de l’algèbre linéaire.

  • multiplication matricielle : %*%;
  • transposition : t;
  • inversion : solve (en fait solve résout A %*% x = B, mais par défaut B est la matrice identité);
  • produit vectoriel (en anglais cross product) de matrices : crossprod;
  • produit dyadique généralisé (en anglais outer product) : outer, %o%;
  • produit de Kronecker généralisé : kronecker, %x%;
  • matrices diagonales : diag;
  • déterminant : det;
  • valeurs et vecteur propres : eigen;
  • décompositions : svd, qr, chol.

5.1.1 Exemples

Faisons quelques exemples pour illustrer certaines de ces fonctions.

5.1.1.1 Opérateur %*%

L’opérateur usuel de multiplication effectue une multiplication terme à terme entre deux matrices.

A <- matrix(1:6, nrow = 3, ncol = 2)
A
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6
B <- matrix(6:1, nrow = 3, ncol = 2)
B
##      [,1] [,2]
## [1,]    6    3
## [2,]    5    2
## [3,]    4    1
A*B
##      [,1] [,2]
## [1,]    6   12
## [2,]   10   10
## [3,]   12    6

Pour effectuer une multiplication matricielle, il faut utiliser l’opérateur %*%. Les dimensions des matrices doivent évidemment concorder.

A %*% B
## Error in A %*% B: non-conformable arguments
C <- matrix(c(5, 2, 3, 7), nrow = 2, ncol = 2)
C
##      [,1] [,2]
## [1,]    5    3
## [2,]    2    7
A %*% C
##      [,1] [,2]
## [1,]   13   31
## [2,]   20   41
## [3,]   27   51

5.1.1.2 Fonction solve

L’inverse d’une matrice s’obtient avec la fonction solve.

solve(C)
##             [,1]       [,2]
## [1,]  0.24137931 -0.1034483
## [2,] -0.06896552  0.1724138

5.1.1.3 Fonction crossprod

La fonction crossprod sert à calculer \(A^T B\) ou \(A^T A\).

crossprod(A, B)
##      [,1] [,2]
## [1,]   28   10
## [2,]   73   28
# équivalent à
t(A) %*% B
##      [,1] [,2]
## [1,]   28   10
## [2,]   73   28

5.1.1.4 Produits dyadique et de Kronecker

Parfois, nous avons besoin d’effectuer une opération en prenant toutes les paires de termes possibles entre deux vecteurs ou matrices. C’est ce que font les produits dyadique (outer product) (opérateur %o%) et de Kronecker (opérateur %x%). Cependant, ils n’assemblent pas les résultats de la même façon. Voici des exemples avec des vecteurs.

1:3 %o% 4:5
##      [,1] [,2]
## [1,]    4    5
## [2,]    8   10
## [3,]   12   15
1:3 %x% 4:5
## [1]  4  5  8 10 12 15

Les deux commandes ont permis le calcul des mêmes 6 produits (\(1 \times 4 = 4\), \(2 \times 4 = 8\), \(3 \times 4 = 12\), \(1 \times 5 = 5\), \(2 \times 5 = 10\) et \(3 \times 5 = 15\)). Cependant, l’opérateur %o% a rassemblé les produits dans une matrice de dimension 3 par 2, et l’opérateur %x% dans un vecteur de longueur \(3 \times 2 = 6\).

Avec deux matrices en entrée, le résultat de A %o% B est un array à 4 dimensions dont les tailles sont, dans l’ordre, nrow(A), ncol(A), nrow(B) et ncol(B). Le résultat de A %x% B est pour sa part une matrice à 2 dimensions comprenant nrow(A)*nrow(B) lignes et ncol(A)*ncol(B) colonnes.

Voici des exemples.

A <- matrix(12:1, nrow = 3, ncol = 4)
A
##      [,1] [,2] [,3] [,4]
## [1,]   12    9    6    3
## [2,]   11    8    5    2
## [3,]   10    7    4    1
B <- matrix(c(1,2), nrow = 2, ncol = 1)
B
##      [,1]
## [1,]    1
## [2,]    2
A %o% B
## , , 1, 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]   12    9    6    3
## [2,]   11    8    5    2
## [3,]   10    7    4    1
## 
## , , 2, 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]   24   18   12    6
## [2,]   22   16   10    4
## [3,]   20   14    8    2
A %x% B
##      [,1] [,2] [,3] [,4]
## [1,]   12    9    6    3
## [2,]   24   18   12    6
## [3,]   11    8    5    2
## [4,]   22   16   10    4
## [5,]   10    7    4    1
## [6,]   20   14    8    2

Les deux opérations se généralisent à l’emploi d’un autre opérateur que le produit, grâce aux fonctions outer et kronecker.

outer(1:3, 4:5, FUN = '+')
##      [,1] [,2]
## [1,]    5    6
## [2,]    6    7
## [3,]    7    8
kronecker(1:3, 4:5, FUN = '+')
## [1] 5 6 6 7 7 8

5.1.1.5 Fonction diag

Finalement, la fonction diag a plusieurs utilités. Selon le type de l’objet qu’elle reçoit comme premier argument, elle permet de :

  • matrice en entrée : extraire la diagonale de la matrice reçue;
C
##      [,1] [,2]
## [1,]    5    3
## [2,]    2    7
diag(C)
## [1] 5 7
  • vecteur en entrée : créer une matrice diagonale à partir du vecteur reçu, qui doit contenir les éléments à mettre sur la diagonale;
diag(1:3)
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    2    0
## [3,]    0    0    3
  • un seul nombre en entrée : créer une matrice identité dont la taille commune des dimensions est déterminée par le nombre fourni.
diag(3)
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

5.2 Calcul différentiel et intégral

(Ce qui est offert en R dans ce domaine n’est pas très performant ni facile d’utilisation.)

5.2.1 Dérivation symbolique : D, deriv et deriv3

Tout comme les logiciels Maple ou Mathematica, R peut faire du calcul symbolique de dérivées. Cependant, il est loin d’être le meilleur outil pour ces tâches. Pour illustrer les capacités (limitées) de R dans ce domaine, tentons d’abord de calculer la dérivée suivante :

\(\frac{d}{dx}( log(x) + sin(x) ).\)

df <- deriv(expr = ~ log(x) + sin(x), namevec = "x")
df
## expression({
##     .value <- log(x) + sin(x)
##     .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
##     .grad[, "x"] <- 1/x + cos(x)
##     attr(.value, "gradient") <- .grad
##     .value
## })

L’objet df est particulier. Il s’agit d’une expression. La ligne .grad[, "x"] <- 1/x + cos(x) permet de constater que R a bien trouvé que la dérivée symbolique de \(log(x) + sin(x)\) est \(1/x + cos(x)\). Nous pouvons maintenant utiliser df pour calculer cette dérivée en certains points. Étant donné que nous avons nommé x la variable dans la fonction à dériver, il faut d’abord créer un objet nommé x contenant les valeurs en lesquelles nous souhaitons calculer la dérivée.

x <- 2:5

Ensuite, nous soumettons la commande suivante pour obtenir le résultat recherché.

eval(df)
## [1] 1.6024446 1.2397323 0.6294919 0.6505136
## attr(,"gradient")
##                x
## [1,]  0.08385316
## [2,] -0.65665916
## [3,] -0.40364362
## [4,]  0.48366219

Cette sortie contient les valeurs de la fonction d’origine aux points d’intérêt,

log(x) + sin(x)
## [1] 1.6024446 1.2397323 0.6294919 0.6505136

suivies des valeurs de la dérivée de la fonction en ces points.

1/x + cos(x)
## [1]  0.08385316 -0.65665916 -0.40364362  0.48366219

Ainsi, R peut faire du calcul symbolique de dérivée, mais il n’offre pas une façon très conviviale de le faire. Plus d’information peut être trouvée dans la fiche d’aide des fonctions D, deriv et deriv3. Le R de base n’offre pas de fonctions pour le calcul symbolique d’intégrales. Cependant, le package Ryacas en offre : https://CRAN.R-project.org/package=Ryacas

5.2.2 Dérivation numérique : numericDeriv

Le calcul de dérivées numériques est un peu plus simple. Par exemple, dérivons la fonction de répartition d’une loi normale standard en quelques points avec la fonction numericDeriv. Cette fonction de répartition est implémentée dans la fonction R pnorm, qui sera vue dans les notes sur les calculs statistiques.

# Points en lesquels nous allons dériver
x <- as.double(-3:3)
# Valeur de la fonction en ces points
pnorm(x)
## [1] 0.001349898 0.022750132 0.158655254 0.500000000 0.841344746 0.977249868 0.998650102
# Calcul de la dérivée en ces points
numericDeriv(expr = quote(pnorm(x)), theta = "x")
## [1] 0.001349898 0.022750132 0.158655254 0.500000000 0.841344746 0.977249868 0.998650102
## attr(,"gradient")
##             [,1]       [,2]      [,3]      [,4]      [,5]       [,6]        [,7]
## [1,] 0.004431849 0.00000000 0.0000000 0.0000000 0.0000000 0.00000000 0.000000000
## [2,] 0.000000000 0.05399097 0.0000000 0.0000000 0.0000000 0.00000000 0.000000000
## [3,] 0.000000000 0.00000000 0.2419707 0.0000000 0.0000000 0.00000000 0.000000000
## [4,] 0.000000000 0.00000000 0.0000000 0.3989423 0.0000000 0.00000000 0.000000000
## [5,] 0.000000000 0.00000000 0.0000000 0.0000000 0.2419707 0.00000000 0.000000000
## [6,] 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.05399096 0.000000000
## [7,] 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.00000000 0.004431849

Nous arrivons au bon résultat, soit la fonction de densité de loi normale standard aux mêmes points. Cette fonction de densité est implémentée dans la fonction R dnorm, qui sera aussi vue dans les notes sur les calculs statistiques.

dnorm(x)
## [1] 0.004431848 0.053990967 0.241970725 0.398942280 0.241970725 0.053990967 0.004431848

L’appel de la fonction numericDeriv n’est pas standard. Il fait intervenir une expression R à créer avec la fonction quote.

Nous pourrions aussi programmer à la main une version simpliste de la dérivation numérique comme suit :

delta <- .000001
(pnorm(x + delta) - pnorm(x - delta)) / (2 * delta)
## [1] 0.004431848 0.053990967 0.241970724 0.398942280 0.241970725 0.053990967 0.004431848

5.2.3 Intégration numérique : integrate

Effectuons maintenant l’opération inverse : intégrons la fonction de densité de la loi normale standard avec la fonction integrate.

integrate(f = dnorm, lower = -Inf, upper = 1)
## 0.8413448 with absolute error < 1.5e-05

Nous arrivons au bon résultat, soit la fonction de répartition de loi normale standard au point 1

pnorm(1)
## [1] 0.8413447

Remarque : La fonction integrate ne travaille pas de façon vectorielle. Elle ne peut pas calculer des intégrales numériques pour plusieurs intervalles en un seul appel de la fonction.

5.3 Optimisation numérique

En mathématiques, l’optimisation consiste à trouver en quel(s) point(s) une fonction mathématique atteint sa valeur maximale ou minimale. En statistique, ce problème est souvent abordé en ces termes : trouver les valeurs des paramètres pour lesquels une fonction atteint son maximum ou son minimum.

Parfois, il est possible de trouver une solution algébrique à ce problème à l’aide du calcul différentiel et intégral. Par contre, il arrive qu’il soit trop difficile, voire impossible, de dériver la fonction en question. L’optimisation numérique est une bonne solution dans un tel cas.

Fonctions R utiles en optimisation numérique :

  • pour optimiser une fonction à une variable : optimize,
  • pour optimiser une fonction avec un nombre de variables quelconque : nlm, optim,
  • optimisation sous contrainte : constrOptim.

Exemple d’optimisation d’une fonction à une variable en R : trouvons en quel point la fonction de densité de la loi normale atteint son maximum. La théorie nous dit que ce maximum est atteint en la valeur de l’espérance de la loi. Voyons si l’optimisation numérique saura retourner le bon résultat.

curve(
  expr = dnorm(x, mean = 3), from = -3, to = 10, 
  main = "Maximum de la densité normale", ylab = "densité N(3,1)"
)
abline(v = 3, lty = 2, col = "blue")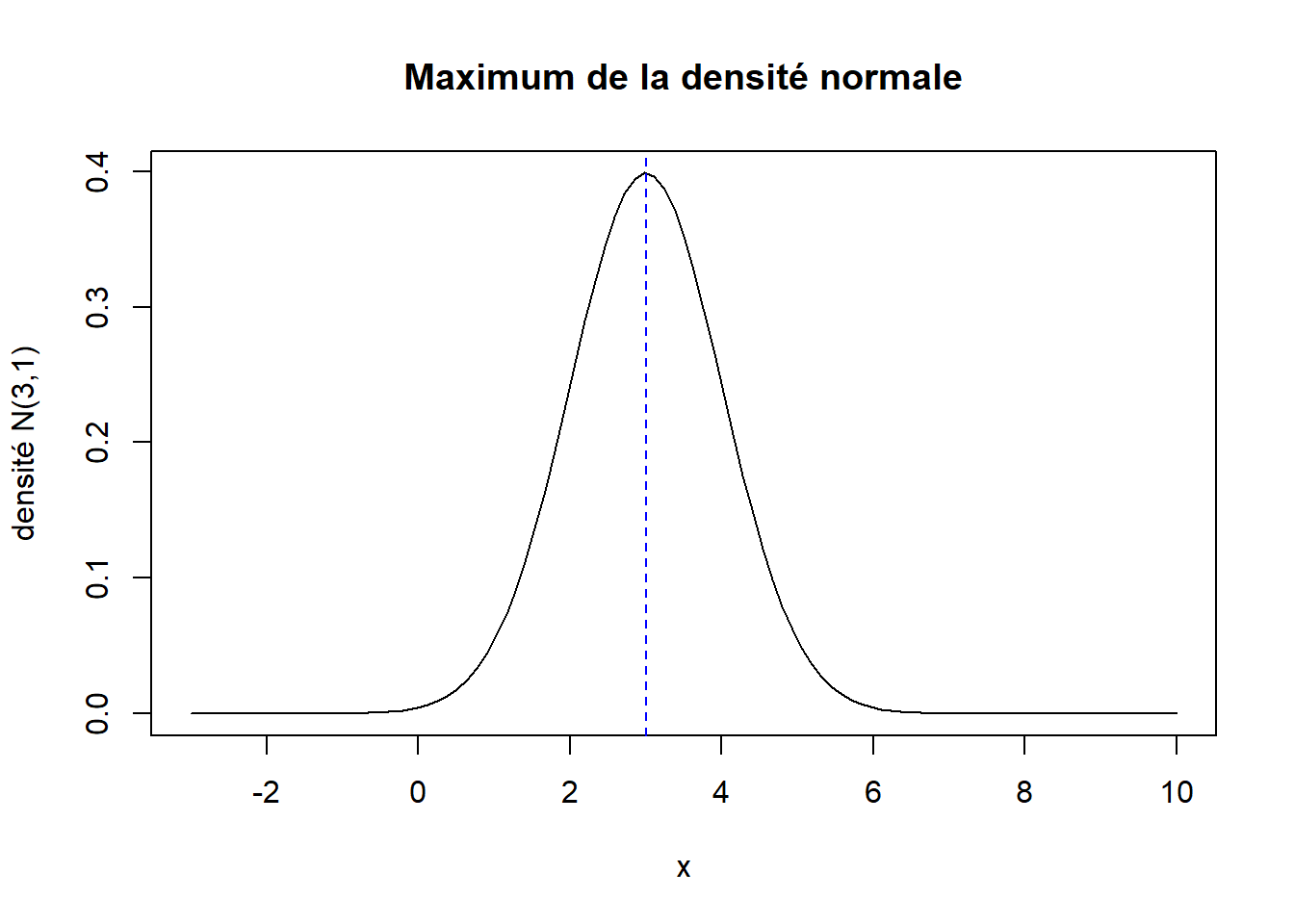

optimize(f = dnorm, interval = c(-3, 10), mean = 3, maximum = TRUE)
## $maximum
## [1] 3
## 
## $objective
## [1] 0.3989423

Oui, pour une loi normale d’espérance 3 et de variance 1, nous arrivons bien numériquement au résultat que le maximum de la densité est atteint en la valeur 3. La fonction optimize nous dit aussi que ce maximum vaut :

dnorm(3, mean = 3)
## [1] 0.3989423

Les fonctions nlm, optim et constrOptim utilisent des algorithmes itératifs. Elles ont besoin de valeurs initiales pour les paramètres (argument par à fournir obligatoirement). À chaque itération de l’algorithme, elles modifient ces valeurs en tentant de se diriger vers l’optimum de la fonction. Elles peuvent :

  • ne pas converger,
  • converger au mauvais endroit (optimum local plutôt que global).

Il faut être prudent lors de leur utilisation. Par exemple, optim est sensible au choix de plusieurs arguments, notamment :

  • l’algorithme employé,
  • les valeurs initiales données aux paramètres.

Ces fonctions sont tout de même très utiles pour effectuer une optimisation lorsque celle-ci est difficile ou impossible à réaliser algébriquement.

Voici un exemple d’optimisation d’une fonction à plusieurs variables. La fonction lm minimise le critère des moindres carrés, en implémentant des formules algébriques. Les estimations des paramètres du modèle linéaire que lm retourne sont les points en lesquelles la fonction des moindres carrés est minimisée. Tentons de minimiser cette fonction de façon numérique. Pour ce faire, nous avons d’abord besoin d’une fonction qui calcule le critère des moindres carrés et qui prend comme premier argument les paramètres du modèle. Nous n’avons pas encore vu dans le cours comment créer des fonctions, mais je me permets tout de même ici d’en créer une, pour illustrer l’optimisation numérique. La syntaxe pour créer des fonctions R sera vue au prochain cours.

Le critère des moindres carrés est calculé en sommant les différences au carré entre les valeurs observées d’une variable et les valeurs prédites par le modèle. Pour un modèle de régression linéaire, la fonction suivante calcule de façon matricielle la valeur du critère.

moindresCarres <- function(beta, y, X) {
  as.vector(crossprod(y - X %*% matrix(beta, ncol = 1)))
}

Le vecteur y doit contenir les valeurs observées de la variable réponse et la matrice X est la matrice de design du modèle. Cette dernière contient les observations des variables explicatives pour les termes présents dans le modèle. Le vecteur y et la matrice X sont des composantes du modèle supposées connues ici. C’est le vecteur de paramètre beta que nous cherchons à estimer. Nous allons utiliser les données du jeu de données cars dans cet exemple.

Voyons d’abord le résultat obtenu avec la fonction lm pour un modèle quadratique.

reg <- lm(dist ~ speed + I(speed^2), data = cars)
coefficients(reg)
## (Intercept)       speed  I(speed^2) 
##   2.4701378   0.9132876   0.0999593

Pour retrouver ce résultat par optimisation numérique, il faut d’abord construire le vecteur y et la matrice X comme suit.

y <- cars$dist
X <- cbind(intercept = 1, cars$speed, cars$speed^2)

La fonction lm arrive à la valeur minimale des moindres carrés suivante

moindresCarres(beta = coefficients(reg), y = y, X = X)
## [1] 10824.72

pour les valeurs de paramètres \(\beta\) = (2.4701378, 0.9132876, 0.0999593). Quel résultat est obtenu avec optim?

op1 <- optim(par = c(3,3,3), fn = moindresCarres, y = y, X = X)
op1
## $par
## [1] 7.2212674 0.2859028 0.1191485
## 
## $value
## [1] 10848.71
## 
## $counts
## function gradient 
##      144       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

L’algorithme a convergé (car il retourne une valeur de 0 pour l’élément convergence dans la sortie), mais il n’arrive pas au bon résultat.

Solution potentielle : changer d’algorithme d’optimisation.

op2 <- optim(par = c(3,3,3), fn = moindresCarres, y = y, X = X, method = "BFGS")
op2
## $par
## [1] 2.47011519 0.91329056 0.09995889
## 
## $value
## [1] 10824.72
## 
## $counts
## function gradient 
##       43        6 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

Autre solution potentielle : changer les bornes initiales.

op3 <- optim(par = c(2.5,1,0.1), fn = moindresCarres, y = y, X = X)
op3
## $par
## [1] 2.46514183 0.91414522 0.09993205
## 
## $value
## [1] 10824.72
## 
## $counts
## function gradient 
##      150       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

Ici, même en partant de valeurs initiales très proches des paramètres optimaux, l’algorithme d’optimisation utilisé par défaut avec optim n’arrive pas tout à fait à trouver l’optimum global de la fonction. Seule la solution de changer l’algorithme d’optimisation nous permet d’arriver approximativement au même résultat que celui trouvé algébriquement par lm.

coefficients(reg)
## (Intercept)       speed  I(speed^2) 
##   2.4701378   0.9132876   0.0999593
op2$par
## [1] 2.47011519 0.91329056 0.09995889

Cet exemple illustre comment la fonction optim s’emploie. Il faut d’abord lui donner en entrée des valeurs initiales pour les paramètres de la fonction à optimiser (argument par). Ensuite, il faut lui fournir la fonction R qui implémente la fonction mathématique à optimiser (argument fn). Cette fonction doit retourner une seule valeur, numérique. De plus, son premier argument doit obligatoirement être le vecteur des paramètres que nous cherchons à estimer par l’optimisation effectuée. Après les arguments par et fn, il faut fournir, au besoin, des arguments à passer à la fonction donnée en entrée via l’argument fn (les arguments y et X dans l’exemple). Finalement, nous pouvons configurer le fonctionnement de la fonction optim en modifiant les valeurs des arguments method, lower, upper, control, ou hessian.

6 Résumé

  • Fonctionnement vectoriel et règle de recyclage : calculs élément par élément pour un objet, ou encore terme à terme entre des objets;

Fonctions et opérateurs mathématiques de base en R

Calcul opère de façon vectorielle combine, retourne une valeur combine, retourne un vecteur
arithmétique +, -, *, /, ^, %%, %/% sum, prod cumsum, cumprod, diff
comparaison ==, !=, >, >=, <, <=
logique !, &, |, xor &&, ||

Conditions logiques

Fonctions opérant de façon vectorielle :

Fonctions retournant toujours un logique de longueur 1 :

  • Opérateurs logiques non vectoriels : && (et), || (ou), isTRUE, isFALSE.
  • Fonctions qui condensent un vecteur logique en une seule valeur logique : all, any.
  • Fonctions de vérification de type :
    is.(numeric/character/logical/vector/matrix/array/list/data.frame/factor/null/…)
    (il en existe beaucoup!).

Comparaison de deux objets R

  • Pour comparer uniquement données contenues dans deux objets atomiques, pas les métadonnées (attributs) : all(x == y).
  • Pour comparer deux objets dans leur totalité (éléments, attributs, type de l’objet et de ses éléments) : identical(x, y).
  • Pour comparer tous les éléments et les attributs de deux objets, en acceptant des différences dans les données numériques selon une certaine tolérance : all.equal(x, y).

 

(Non évalué à partir d’ici.)

Algèbre linéaire

  • multiplication matricielle : %*%;
  • transposition : t;
  • inverse : solve (en fait solve résout A %*% x = B, mais par défaut B est la matrice identité);
  • produit vectoriel (en anglais cross product) de matrices : crossprod;
  • produit dyadique généralisé (en anglais outer product) : outer, %o%;
  • produit de Kronecker généralisé : kronecker, %x%;
  • matrices diagonales : diag;
  • déterminant : det;
  • valeurs et vecteur propres : eigen;
  • décompositions : svd, qr, chol.

Calcul différentiel et intégral

Optimisation numérique

Définition générale : Trouver en quel(s) point(s) une fonction mathématique atteint sa valeur maximale ou minimale.

Application usuelle en statistique : Trouver les valeurs des paramètres pour lesquels une fonction (ex. log-vraisemblance ou somme des erreurs au carré) atteint son maximum ou son minimum.

  • pour optimiser une fonction à une variable : optimize,
  • pour optimiser une fonction avec un nombre de variables quelconque : nlm, optim,
  • optimisation sous contrainte : constrOptim.

Ces fonctions prennent en entrée une fonction R

  • dont le premier argument est le vecteur des paramètres et
  • dont la sortie est une seule valeur numérique, soit la valeur prise par la fonction mathématique à optimiser lorsque les paramètres prennent les valeurs fournies en entrée.

Références

Les informations présentées dans ces notes proviennent des fiches d’aide du logiciel R :

  • R Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/

Pour aller plus loin :

  • Braun, W. J. et Murdoch, D. (2007). A first Course in Statistical Programming with R. Cambridge University Press.