Optimisation de temps d'exécution en R

Sophie Baillargeon, Université Laval

2021-04-03

Version PDF de cette page web : optim_temps_r_2021.pdf

Note préliminaire : Lors de leur dernière mise à jour, ces notes ont été révisées en utilisant R version 4.0.3, le package bench version 1.1.1 (et le package beeswarm version 0.3.1 utilisé par la méthode plot.bench_mark), le package profvis version 0.3.7, le package data.table version 1.13.6 et le package parallel version 4.0.3. Pour d’autres versions, les informations peuvent différer.

Lorsque nous écrivons du code, notre but premier est évidemment que ce code fonctionne correctement. Après avoir vérifié que le code produit les résultats escomptés et gère correctement les exceptions, nous devrions, selon les bonnes pratiques, nous assurer que le code est facile à maintenir (écriture, compréhension et réutilisation aisées). Si notre code remplit toutes les conditions énumérées ci-dessus, mais que son temps d’exécution est long, nous devrions envisager de le rendre plus rapide, sans quoi il risque d’être peu ou pas utilisé. Cependant, n’oublions pas qu’il est inutile d’optimiser le temps d’exécution d’un programme roulant déjà suffisamment rapidement.

Pour réduire le temps d’exécution d’un programme, il faut d’abord cerner la partie du programme responsable des lenteurs. Pour ce faire, il est conseillé d’utiliser des outils qui analysent la performance du code. Après avoir cerné les instructions problématiques, il faut les modifier de façon à effectuer le calcul plus rapidement. Certains outils d’analyse de performance sont présentés dans ce qui suit. Ensuite, nous verrons des stratégies d’optimisation de temps d’exécution.

1 Outils d’analyse de la performance d’un programme R

Une analyse de la performance d’un programme informatique est appelée profilage de code (en anglais code profiling). Il est possible de profiler l’utilisation du processeur et l’utilisation de la mémoire. Nous nous attarderons surtout ici au profilage de l’utilisation du processeur, qui vise principalement à évaluer le temps d’exécution d’un programme. Cependant, nous parlerons aussi un peu de profilage d’utilisation de la mémoire, car la gestion de la mémoire a un impact sur le temps d’exécution.

Le R de base propose deux outils pour effectuer du profilage d’utilisation du processeur :

  • la fonction system.time : pour le calcul de temps global d’exécution;
  • les fonctions Rprof et summaryRprof : pour décortiquer la provenance des lenteurs dans un code R.

Cependant, ces fonctions sont souvent insuffisantes pour réaliser une analyse approfondie. Nous utiliserons aussi les packages suivants :

  • bench : pour le calcul de temps global d’exécution et un suivi de la gestion de la mémoire;
  • profvis : pour visualiser le résultat produit par Rprof.

Pour illustrer l’utilisation de ces fonctions, nous allons reprendre un exemple des notes sur les fonctions en R. Nous avions créé les deux fonctions suivantes pour compter combien de nombres entiers impairs contient un vecteur numérique [1].

#' @title Compte le nombre d'entiers impairs dans un vecteur numérique
#' @description Version avec calcul vectoriel
#' @param x vecteur numérique
#' @return le nombre de nombres entiers impairs dans x
compte_impair_vectoriel <- function(x) {
  sum(x %% 2 == 1)
}
#' @inherit compte_impair_vectoriel title params return
#' @description Version avec boucle
compte_impair_boucle <- function(x) {
  k <- 0
  for (n in x) {
    if (n %% 2 == 1) {
      k <- k + 1
    }
  }
  k
}

Des tags roxygen2 sont utilisés pour documenter les fonctions. Cependant, les commentaires roxygen écrits ici ne formeraient pas des fiches d’aide complètes. Ce n’est pas un problème puisque nous n’avons pas l’intention de créer un package avec ces fonctions. Notons que le tag @inherit permet de reprendre telles quelles des sections d’une autre fiche d’aide, ici le titre, la description des arguments et de la sortie.

Avant de profiler ces fonctions, assurons-nous qu’elles retournent le même résultat. Pour ce faire, donnons-leur en entrée un vecteur obs contenant un million d’observations générées aléatoirement.

# Génération aléatoire d'un million d'observations
obs <- round(runif(1000000, -10, 10))
# Appels aux fonctions à comparer
compte_1 <- compte_impair_vectoriel(x = obs)
compte_2 <- compte_impair_boucle(x = obs)
# Comparaison des sorties retournées
compte_1 == compte_2
## [1] TRUE

Les deux fonctions retournent bien dans cet exemple la même valeur numérique. Notons cependant que la première fonction (compte_impair_vectoriel) retourne le résultat sous la forme d’un entier (integer) et la deuxième (compte_impair_boucle) sous la forme d’un réel (double). Cette différence de type de donnée retournée n’est pas un problème ici.

1.1 Fonction system.time

Mesurons combien de temps prennent les exécutions d’appels aux fonctions compte_impair_vectoriel et compte_impair_boucle lorsque nous leur donnons en entrée le vecteur obs. Pour ce faire, utilisons d’abord la fonction system.time, comme nous l’avions fait dans les notes sur les fonctions en R.

temps_1 <- system.time(compte_1 <- compte_impair_vectoriel(x = obs))
temps_2 <- system.time(compte_2 <- compte_impair_boucle(x = obs))

Il faut donner en entrée à system.time une instruction R, contenant ou non une assignation, ou encore des instructions R encadrées d’accolades. Cet ensemble d’instruction(s) est appelé expression. La fonction retourne le temps, en secondes, d’utilisation du CPU (Central Processing Unit) pour l’exécution de l’expression. Notons que le terme « exécution » pourrait être remplacé par le terme « évaluation ». Ils ont ici la même signification.

J’obtiens les temps suivants, qui indiquent que compte_impair_vectoriel est plus rapide que compte_impair_boucle :

temps_1
##    user  system elapsed 
##    0.00    0.01    0.03
temps_2
##    user  system elapsed 
##    0.23    0.02    0.25

Les trois temps dans une sortie produite par system.time peuvent être définis ainsi :

  • user : temps écoulé par le logiciel R (calling process) pour évaluer l’expression;
  • system : temps écoulé par le système d’exploitation de notre ordinateur, mais pour le compte du logiciel R, pendant l’exécution de l’expression;
  • elapsed : temps total écoulé entre la soumission de l’expression et le retour du résultat (possiblement plus grand que la somme des deux autres temps, car le système a peut-être dû accorder du temps à d’autres processus actifs sur l’ordinateur pendant l’exécution de l’expression)

Les temps d’exécution obtenus dépendent des spécifications de l’ordinateur utilisé, en particulier de la puissance de son CPU. De plus, nous n’obtiendrons probablement pas exactement les mêmes temps si nous évaluons à nouveau l’expression. Il y a une petite variation normale du temps d’exécution, causée notamment par les autres processus utilisant le CPU de notre ordinateur au moment où la commande est lancée.

1.2 Package bench

La fonction system.time est plutôt minimaliste. Elle mesure le temps pris par une seule exécution d’une expression. Pour évaluer plus justement le temps d’exécution d’une expression, il est préférable de l’exécuter à quelques reprises, puis de calculer le temps médian d’exécution. La médiane est plus appropriée que la moyenne pour cette mesure de tendance centrale, car elle est robuste aux valeurs extrêmes, qui ne sont pas si rares parmi des temps d’exécution. Aussi, étant donné qu’il y a un lien entre le temps d’exécution et la gestion de la mémoire, il serait pertinent de récolter, en plus du temps, des informations concernant la mémoire utilisée pendant les exécutions. Voilà le but du package bench. Dans ces notes, nous allons utiliser la fonction mark de ce package pour effectuer du profilage de plusieurs fonctions R.

Comparativement à la fonction system.time, la fonction mark possède plusieurs avantages, notamment :

  • profilage de plus d’une expression à la fois;
  • chronométrage plus précis grâce aux répétitions et à une unité de mesure de temps plus fine;
  • suivi de la gestion de la mémoire.

Voici un premier exemple d’utilisation de cette fonction :

library(bench)
sortie_mark <- mark(
  vectoriel = compte_impair_vectoriel(obs), 
  boucle = compte_impair_boucle(obs)
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.

Un avertissement a été émis. Nous y reviendrons.

Il faut fournir en entrée à cette fonction une série d’expressions à profiler (ce pourrait être une seule expression). Ces expressions sont à fournir en arguments distincts, attrapés par l’argument ..., qui permet le passage d’autant d’expressions à profiler que souhaité. Les expressions peuvent être assignées à des noms avec l’opérateur = (comme dans l’exemple), ou non. Le nom fourni à gauche de l’opérateur = pour une expression est celui utilisé pour identifier l’expression dans la sortie, ce qui peut aider à alléger l’affichage des résultats.

La sortie retournée par la fonction mark a un format particulier. Il s’agit d’un objet possédant 4 classes, dont celle de data frame, mais pour lequel les éléments ne sont pas tous de simples vecteurs ou facteur.

class(sortie_mark)
## [1] "bench_mark" "tbl_df"     "tbl"        "data.frame"
sortie_mark
## # A tibble: 2 x 13
##   expression   min  median `itr/sec` mem_alloc `gc/sec` n_itr  n_gc total_time result
##   <bch:expr> <bch> <bch:t>     <dbl> <bch:byt>    <dbl> <int> <dbl>   <bch:tm> <list>
## 1 vectoriel   19ms  24.7ms     41.6     11.4MB     9.90    21     5      505ms <int ~
## 2 boucle     239ms 310.3ms      3.22        0B    17.7      2    11      621ms <dbl ~
## # ... with 3 more variables: memory <list>, time <list>, gc <list>

Pour simplifier l’analyse des résultats retournés par mark, je vais utiliser la fonction suivante pour imprimer les sorties produites par cette fonction dans le reste de ces notes.

#' @title Impression simplifiée d'une sortie de bench::mark
#' @description Conserve six éléments et imprime sous forme de data frame
#' @param x sortie produite par bench::mark
print_bench_mark <- function(x){
  if (!inherits(x, what = "bench_mark")) {
    stop("'x' n'est pas une sortie de bench::mark")
  }
  df <- data.frame(
    expression = as.character(x$expression),
    n_itr = x$n_itr,
    min = if (inherits(x$min, "bench_time")) as.character(x$min) else x$min,
    median = if (inherits(x$min, "bench_time")) as.character(x$median) else x$median,
    mem_alloc = as.character(x$mem_alloc),
    n_gc = x$n_gc,
    stringsAsFactors = FALSE
  )
  print(df)
  invisible(df)
}
print_bench_mark(sortie_mark)
##   expression n_itr   min  median mem_alloc n_gc
## 1  vectoriel    21  19ms  24.7ms    11.4MB    5
## 2     boucle     2 239ms 310.3ms        0B   11

Dans cette sortie, possédant une ligne par expression à profiler, les différentes colonnes contiennent :

  • expression : identifiant de l’expression,
  • n_itr : nombre de répétitions (ou itérations) de l’exécution de l’expression,
  • min : temps pris par l’exécution la plus rapide de l’expression,
  • median : temps médian d’exécution parmi les répétitions,
  • mem_alloc : quantité totale de mémoire allouée pendant une exécution de l’expression,
  • n_gc : nombre total de récupérations de mémoire (en anglais garbage collections, d’où l’abréviation gc) effectuées pendant toutes les répétitions d’exécution.

Dans cet exemple, la fonction compte_impair_vectoriel est beaucoup plus rapide que la fonction compte_impair_boucle (temps médians de 24.7ms = 0.0247 secondes versus 310.3ms = 0.3103 secondes), mais elle utilise plus de mémoire (11.4MB versus approximativement 0B).

Les unités de temps et de mémoire sont adaptées de façon à ce que les nombres imprimés ne soient pas trop gros, ni trop petits. Ici, la fonction mark a choisi de mesurer le temps en millisecondes (ms). Nous aurions pu demander à mark d’utiliser des unités de temps aussi petites que des nanosecondes (ns) via son argument time_unit. Remarquez que ces unités peuvent varier d’une expression à l’autre, comme c’est le cas pour les unités de mémoire dans l’exemple.

Par défaut, la fonction mark vérifie si les sorties produites par les différentes expressions sont équivalentes avec la fonction all.equal. Dans l’exemple présenté ici, cette vérification est pertinente. Elle ne l’est cependant pas toujours. Parfois, il est normal que les expressions à comparer ne retournent pas des résultats équivalents (p. ex. pas sous le même format). Dans un tel cas, il faut ajouter l’argument check = FALSE dans l’appel à la fonction mark.

La fonction mark sélectionne de façon automatique le nombre de fois qu’est répétée (ou itérée) l’exécution de chacune des expressions. Nous pouvons aussi contrôler ce nombre de répétitions à l’aide des arguments iterations, min_iterations et max_iterations. Pour nous assurer d’effectuer toujours au moins 10 répétitions, nous utiliserons à l’avenir l’argument min_iterations = 10.

sortie_mark <- mark(
  compte_impair_vectoriel(obs), 
  compte_impair_boucle(obs),
  min_iterations = 10
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(sortie_mark)
##                     expression n_itr     min  median mem_alloc n_gc
## 1 compte_impair_vectoriel(obs)    18  18.8ms  27.2ms    11.4MB    4
## 2    compte_impair_boucle(obs)    10 187.8ms 214.3ms        0B   68

Le message d’avertissement "Some expressions had a GC in every iteration; so filtering is disabled.", obtenu lors des deux appels précédents à la fonction mark n’est pas problématique. Dans le calcul du temps médian, la fonction mark cherche à considérer seulement les exécutions pendant lesquelles de la récupération de mémoire n’a pas eu lieu, car celle-ci ralentit l’exécution. Elle est contrainte à ne pas effectuer ce filtrage si toutes les exécutions d’une expression ont subi de la récupération de mémoire. La section suivante explique ce qu’est la récupération de mémoire.

Avant de terminer, le package bench offre même une méthode pour la fonction générique plot permettant de représenter graphiquement les résultats du profilage.

plot(sortie_mark)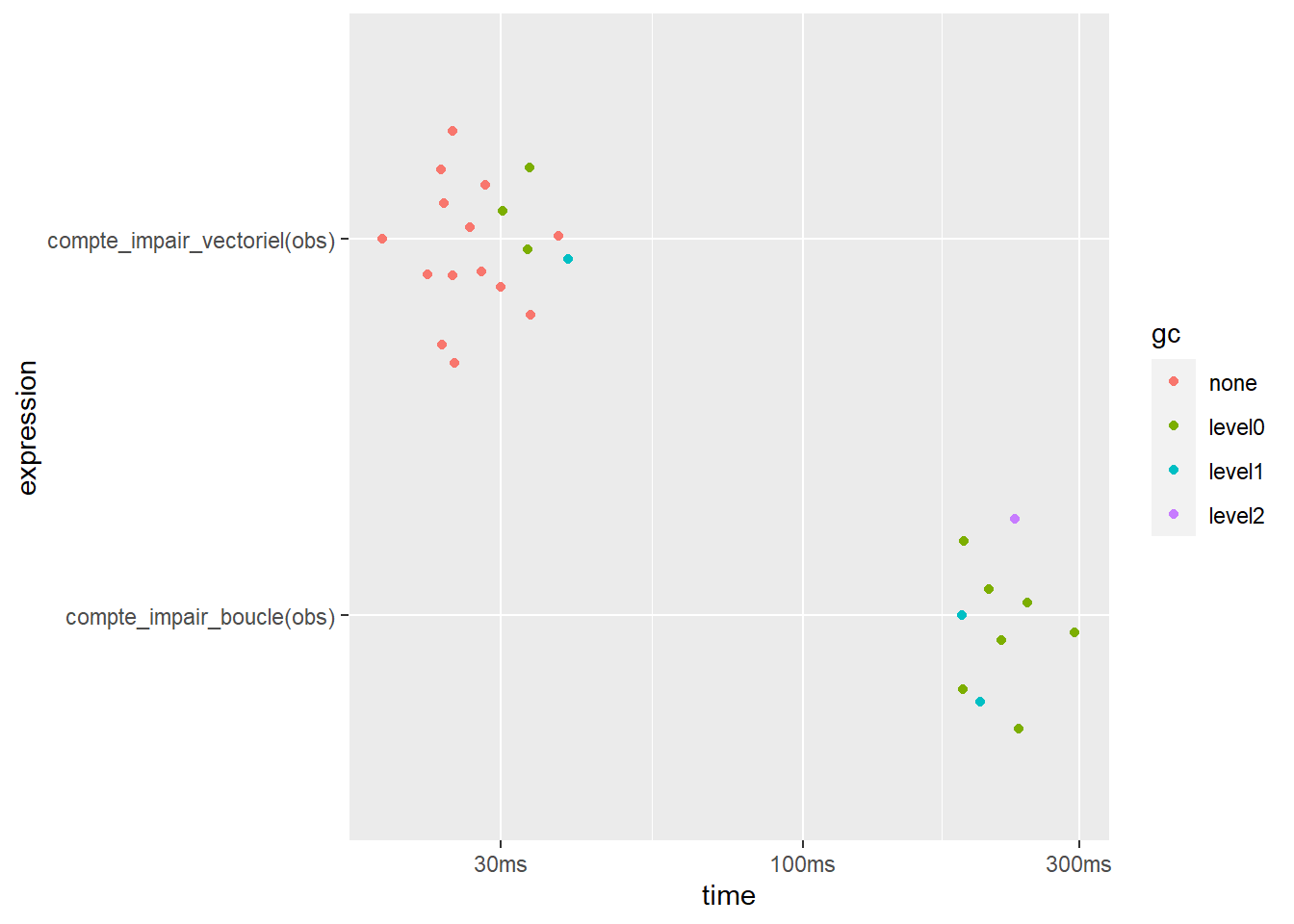

Pour plus d’informations concernant ce graphique et d’autres possibilités du package bench, le lecteur est référé à la documentation du package : http://bench.r-lib.org/.

1.3 Liens entre gestion de la mémoire et temps d’exécution

Il n’est pas rare en R que des solutions soient rapides, mais utilisent beaucoup de mémoire. Comme illustré dans l’exemple précédent, et comme nous l’illustrerons une autre fois plus loin dans ces notes, les calculs matriciels et vectoriels sont souvent des options de calcul optimisés en R. Cependant, ils impliquent la création de matrices ou de vecteurs contenant potentiellement un grand nombre d’éléments. Ainsi, la rapidité a parfois un envers : l’utilisation d’une grande quantité de mémoire. Nous verrons que cette contrepartie peut devenir problématique lors du traitement d’une grande quantité de données. Il faut parfois gérer un compromis entre temps d’exécution et quantité de mémoire utilisée.

Aussi, l’opération d’allouer de l’espace dans la mémoire d’un ordinateur pour stocker des données prend un certain temps à être réalisée. Un programme R qui génère de nombreuses allocations en mémoire aura tendance à être lent. Une des stratégies présentées ici identifie des opérations à éviter en raison du grand nombre d’allocations en mémoire qu’elles provoquent.

1.3.1 Récupération de mémoire

Étant donné que les allocations et désallocations de mémoire en R sont réalisées de façon implicite plutôt qu’explicitement par l’utilisateur comme dans certains langages informatiques (p. ex. en C), R doit s’occuper de libérer périodiquement de façon automatique la mémoire qui n’est plus utilisée. Cette opération s’appelle « récupération de mémoire », en anglais garbage collection ou gc. Il s’agit d’une opération essentielle pour ne pas saturer la mémoire de l’ordinateur pendant une session R.

Tout comme l’allocation de mémoire, la récupération de mémoire prend un peu de temps à être réalisée. Il est donc pertinent de savoir si le récupérateur de mémoire (garbage collector), aussi appelé ramasse-miettes, a été lancé pendant l’exécution d’une expression. Cette opération, dont nous ne contrôlons pas le déclenchement, ralentit légèrement les exécutions.

1.4 Fonctions Rprof et summaryRprof

Les fonctions system.time et mark sont bien pratiques pour évaluer un temps global d’exécution. Cependant, elles ne nous aident pas à identifier les parties d’un programme R, typiquement le corps d’une fonction, qui sont les plus lentes. Pour arriver à identifier les instructions causant des lenteurs, il faut plutôt utiliser un outil telles que les fonctions Rprof et summaryRprof.

Pour utiliser ces fonctions, il faut ajouter la commande Rprof() avant le bout de code à minuter et ajouter Rprof(NULL) après le bout de code, comme dans cet exemple :

Rprof(interval = 0.001)
compte_impair_boucle(obs)
Rprof(NULL)

Un fichier a est créé dans notre répertoire de travail. Il se nomme par défaut Rprof.out, mais nous pouvons changer ce nom avec l’argument filename de la fonction Rprof. À chaque 0.001 seconde (argument interval), R a écrit dans ce fichier le nom de la fonction ou des fonctions dont un appel est en cours d’exécution. La fonction Rprof conserve donc une trace de la pile d’exécution (en anglais call stack) à intervalle de temps fixes.

Typiquement, nous n’allons pas voir directement le contenu de ce fichier. Nous en affichons plutôt un résumé avec la fonction summaryRprof comme suit :

summaryRprof("Rprof.out")
## $by.self
##                        self.time self.pct total.time total.pct
## "compte_impair_boucle"     0.095    52.49      0.181    100.00
## "%%"                       0.086    47.51      0.086     47.51
## 
## $by.total
##                        total.time total.pct self.time self.pct
## "compte_impair_boucle"      0.181    100.00     0.095    52.49
## "%%"                        0.086     47.51     0.086    47.51
## 
## $sample.interval
## [1] 0.001
## 
## $sampling.time
## [1] 0.181

Dans cette sortie, les éléments by.self et by.total contiennent les mêmes valeurs, mais pas dans le même ordre (colonnes interchangées). Les colonnes total.time et total.pct réfèrent au temps total passé à l’exécution de l’appel à une fonction. Pour les colonnes self.time et self.pct, le temps d’exécution des appels de fonctions imbriqués dans l’appel de la fonction en question est retiré du temps total.

Dans l’exemple, la commande compte_impair_boucle(x) prend un total de 0.181 seconde à être évaluée. Exécuter un appel à la fonction compte_impair_boucle signifie exécuter le corps de la fonction avec les valeurs d’arguments fournis en entrée. De l’exécution du corps de la fonction compte_impair_boucle, seul l’appel à l’opérateur %% apparaît dans la sortie de summaryRprof. Les appels aux autres fonctions ou opérateurs sont ici tellement rapides qu’ils n’ont pas été détectés par Rprof. Le temps passé à évaluer les appels à l’opérateur %% est de 0.086 seconde. Ainsi, le self.time de compte_impair_boucle est 0.181 - 0.086 = 0.095 seconde.

Afin de mieux expliquer l’interprétation de la sortie de summaryRprof, voyons aussi un autre exemple qui produit une sortie plus longue. Les arguments memory.profiling et gc.profiling de la fonction Rprof sont illustrés.

# Facteur généré aléatoirement pour l'exemple
facteur <- sample(x = 1:10, size = length(obs), replace = TRUE)

# Profilage du temps d'exécution et de la gestion de la mémoire 
# d'un appel à aggregate avec les données simulées
Rprof(interval = 0.01, memory.profiling = TRUE, gc.profiling = TRUE)
res <- aggregate(x = obs, by = list(facteur), FUN = median)
Rprof(NULL)

# Résumé de la sortie de Rprof
summaryRprof("Rprof.out", memory = "both")
## $by.self
##                         self.time self.pct total.time total.pct mem.total
## "[.data.frame"               0.07    24.14       0.18     62.07      77.4
## "<GC>"                       0.06    20.69       0.06     20.69      15.3
## "<Anonymous>"                0.04    13.79       0.05     17.24       7.6
## "anyDuplicated.default"      0.03    10.34       0.03     10.34       8.0
## "unique.default"             0.02     6.90       0.07     24.14      23.6
## "match"                      0.01     3.45       0.07     24.14      27.5
## "split.default"              0.01     3.45       0.02      6.90      34.7
## "as.character.factor"        0.01     3.45       0.01      3.45       0.0
## "complete.cases"             0.01     3.45       0.01      3.45       3.9
## "f"                          0.01     3.45       0.01      3.45       0.0
## "factor"                     0.01     3.45       0.01      3.45      23.3
## "is.na"                      0.01     3.45       0.01      3.45       8.5
## 
## $by.total
##                         total.time total.pct mem.total self.time self.pct
## "aggregate"                   0.28     96.55     144.0      0.00     0.00
## "aggregate.data.frame"        0.28     96.55     144.0      0.00     0.00
## "aggregate.default"           0.28     96.55     144.0      0.00     0.00
## "[.data.frame"                0.18     62.07      77.4      0.07    24.14
## "["                           0.18     62.07      77.4      0.00     0.00
## "unique.default"              0.07     24.14      23.6      0.02     6.90
## "match"                       0.07     24.14      27.5      0.01     3.45
## "sort"                        0.07     24.14      20.3      0.00     0.00
## "<GC>"                        0.06     20.69      15.3      0.06    20.69
## "unique"                      0.06     20.69      11.8      0.00     0.00
## "<Anonymous>"                 0.05     17.24       7.6      0.04    13.79
## "do.call"                     0.05     17.24       7.6      0.00     0.00
## "FUN"                         0.04     13.79      55.1      0.00     0.00
## "lapply"                      0.04     13.79      55.1      0.00     0.00
## "anyDuplicated.default"       0.03     10.34       8.0      0.03    10.34
## "anyDuplicated"               0.03     10.34       8.0      0.00     0.00
## "split.default"               0.02      6.90      34.7      0.01     3.45
## "as.factor"                   0.02      6.90      35.1      0.00     0.00
## "sort.int"                    0.02      6.90      20.3      0.00     0.00
## "split"                       0.02      6.90      34.7      0.00     0.00
## "unname"                      0.02      6.90      34.7      0.00     0.00
## "as.character.factor"         0.01      3.45       0.0      0.01     3.45
## "complete.cases"              0.01      3.45       3.9      0.01     3.45
## "f"                           0.01      3.45       0.0      0.01     3.45
## "factor"                      0.01      3.45      23.3      0.01     3.45
## "is.na"                       0.01      3.45       8.5      0.01     3.45
## ".rs.callAs"                  0.01      3.45       0.0      0.00     0.00
## "as.character"                0.01      3.45       0.0      0.00     0.00
## "doTryCatch"                  0.01      3.45       0.0      0.00     0.00
## "mean"                        0.01      3.45       8.5      0.00     0.00
## "median.default"              0.01      3.45       8.5      0.00     0.00
## "Rprof"                       0.01      3.45       0.0      0.00     0.00
## "sort.default"                0.01      3.45       8.5      0.00     0.00
## "tryCatch"                    0.01      3.45       0.0      0.00     0.00
## "tryCatchList"                0.01      3.45       0.0      0.00     0.00
## "tryCatchOne"                 0.01      3.45       0.0      0.00     0.00
## "withCallingHandlers"         0.01      3.45       0.0      0.00     0.00
## 
## $sample.interval
## [1] 0.01
## 
## $sampling.time
## [1] 0.29

Dans cet exemple, les éléments by.self et by.total ne contiennent pas les mêmes lignes. Les fonctions dont les self.time sont nuls n’apparaissent pas dans l’élément by.self. Nous voyons aussi que les lignes sont ordonnées en ordre décroissant de self.time dans l’élément by.self et en ordre décroissant de total.time dans l’élément by.total.

La colonne mem.total a été ajoutée comparativement à la sortie obtenue dans l’exemple précédent. Elle indique la quantité de mémoire utilisée. Elle est présente en raison de l’argument memory.profiling = TRUE. L’argument gc.profiling = TRUE à quant à lui pour effet de rapporter les temps d’appel au récupérateur de mémoire, identifié par "<GC>", si celui-ci a été lancé.

Nous constatons que le code de la méthode aggregate.data.frame fait appel à un grand nombre de fonctions. Nous n’analyserons pas cette sortie davantage ici. Mentionnons seulement que les méthodes de la fonction générique aggregate ne sont pas vraiment conçues pour être rapides.

1.5 Package profvis

Pour identifier encore plus facilement les lignes les plus lentes de notre code, nous pouvons utiliser le package profvis. Ce package offre en fait une façon de visualiser le résultat produit par Rprof. Voici un exemple de son utilisation.

library(profvis)
profvis({
  compte_impair_boucle <- function(x) {
    k <- 0
    for (n in x) {
      if (n %% 2 == 1){
        k <- k + 1
      } 
    }
    k
  }
  compte_impair_boucle(obs)
})

Pour obtenir le détail du temps d’exécution par ligne du corps d’une de nos fonctions, il faut fournir, dans l’appel à la fonction profvis, le code définissant la fonction en plus de l’instruction appelant la fonction. Remarquez les accolades nécessaires lorsque l’expression à profiler s’étend sur plus d’une ligne. Le résultat obtenu est ouvert dans une fenêtre indépendante, dont voici une copie :

Fenêtre de profilage ouverte par l'exemple d'appel à la fonction profvis précédent

Figure 1.1: Fenêtre de profilage ouverte par l’exemple d’appel à la fonction profvis précédent

RStudio intègre particulièrement bien la fenêtre affichant les résultats d’un appel à la fonction profvis. La figure précédente ne montre qu’un des deux onglets de cette fenêtre, soit l’onglet Flame Graph. La fonction profvis profile à la fois l’utilisation de la mémoire (colonne Memory) et du temps d’exécution (colonne Time).

Dans l’exemple, nous voyons encore clairement que ce sont les appels à l’opérateur %% qui prennent le plus de temps à être évalués dans le corps de la fonction compte_impair_boucle.

Le site web suivant documente l’utilisation du package profvis : http://rstudio.github.io/profvis/.

2 Stratégies d’optimisation du temps d’exécution

Il y a différentes stratégies utiles à connaître pour écrire du code R rapide. Voici une énumération de ces stratégies, qui sont présentées dans les sous-sections suivantes.

  1. Utiliser des fonctions optimisées.
  2. Faire seulement ce qui est nécessaire.
  3. Exploiter les calculs matriciels et vectoriels.
  4. Éviter les allocations de mémoire inutiles.
  5. Faire du calcul en parallèle.
  6. Reprogrammer en C ou C++ les bouts de code les plus lents.

Pour illustrer ces astuces, nous allons souvent utiliser un exemple tiré de Peng et de Leeuw (2002). Il s’agit de fonctions R ayant pour but d’estimer la fonction de densité d’une variable aléatoire par la méthode du noyau à partir d’observations de la variable aléatoire. De l’information sur cette méthode, appelée en anglais Kernel density estimation, peut être trouvée sur la page Wikipédia suivante : https://fr.wikipedia.org/wiki/Estimation_par_noyau.

Il existe en fait déjà une fonction dans le package stats pour faire de l’estimation de densité par noyau : la fonction density, déjà vue dans les notes sur les graphiques. Voici un exemple de ce qu’il est possible de réaliser avec cette fonction.

dens <- density(x = faithful$eruptions)  # faithful provient du package datasets
hist(
  x = faithful$eruptions, 
  freq = FALSE,
  xlab = "durées des éruptions",
  ylab = "densité",
  main = "Densité empirique des durées des éruptions du geyser Old Faithful",
  cex.main = 0.9
)
lines(dens)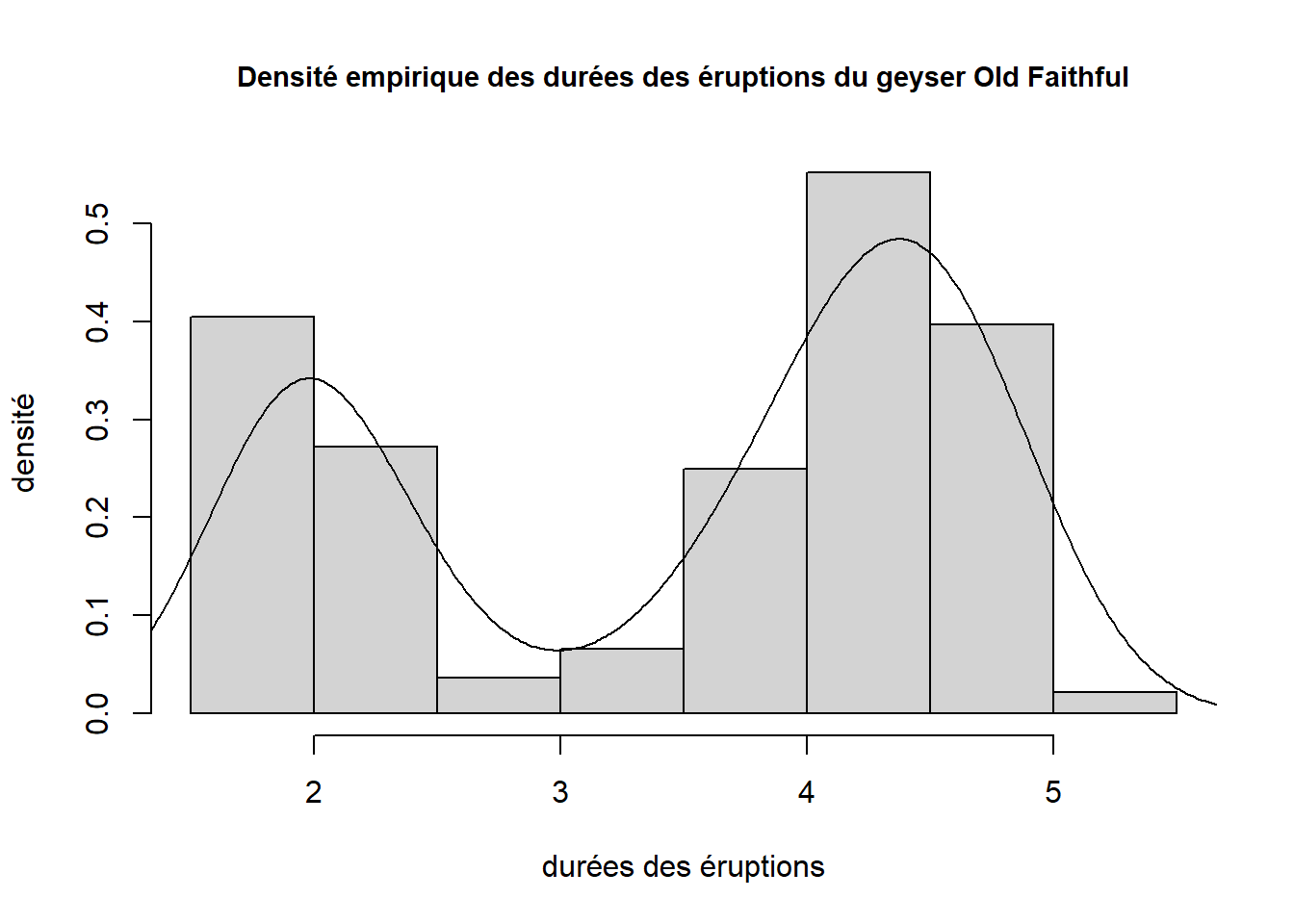

Un histogramme est aussi une méthode d’estimation de densité. Ici, nous avons superposé une courbe de densité estimée par la méthode du noyau (aussi appelée densité Kernel) à un histogramme.

Nous allons écrire une version moins puissante de la fonction density. L’estimation de densité par noyau au point \(x\) se fait par la formule suivante :

\(\hat{f}(x) = \frac{1}{nh} \sum_{i = 1}^n K \left( \frac{x - x_i}{h} \right)\)

où \(x_i\) pour \(i=1, 2, \ldots, n\) sont les observations, \(K\) est une fonction noyau (en anglais kernel) à définir et \(h\) est un paramètre de lissage (parfois appelée fenêtre). Plus la valeur de \(h\) est grande, plus la courbe obtenue est lisse.

La fonction density permet l’utilisation de plusieurs fonctions noyau via l’argument kernel. Nous allons plutôt nous restreindre au noyau gaussien, qui est en fait la fonction de densité d’une distribution normale standard. Nous allons donc utiliser la fonction dnorm pour évaluer la fonction \(K\) dans la formule ci-dessus.

Voici la première fonction proposée.

#' @title Estimation de densité par noyau gaussien
#' @description Version 1 : utilisation de 2 boucles imbriquées
#' @param x vecteur numérique contenant les observations
#' @param xpts vecteur numérique contenant les points en lesquels l'estimation de la 
#'             densité doit être effectuée
#' @param h nombre réel > 0 : la valeur du paramètre de lissage
#' @return vecteur numérique contenant la densité estimée en tous les points de xpts
ksmooth_double_loop <- function(x, xpts, h) 
{
  dens <- double(length(xpts))
  n <- length(x)
  for(i in 1:length(xpts)) {
    ksum <- 0
    for(j in 1:length(x)) {
      d <- xpts[i] - x[j]
      ksum <- ksum + dnorm(d / h)
    }
    dens[i] <- ksum / (n * h)
  }
  dens
}

Dans la fonction ksmooth_double_loop, le premier argument, nommé x, n’est pas équivalent au \(x\) de la formule. Le \(x\) de la formule représente un point en lequel nous souhaitons faire l’estimation. Son équivalent dans la fonction ksmooth_double_loop est donc un élément du vecteur xpts. Ce sont les \(x_i\) de la formule que nous retrouvons dans le vecteur x. Dans la boucle, ce vecteur x est parcouru en utilisant l’indice j. Alors, en fait, x[j] dans le corps de la fonction représente un \(x_i\) dans la formule. Le code aurait pu coller davantage à la notation dans la formule pour être encore plus clair, mais j’ai choisi de le conserver tel qu’il a été proposé dans Peng et de Leeuw (2002). Tout ce que j’ai changé ici par rapport à cette référence est le nom de la fonction. J’ai renommé ksmooth_double_loop la fonction que Peng et de Leeuw (2002) ont nommé ksmooth1.

Notons que nous pouvons considérer ici que la fonction ksmooth_double_loop a d’abord été testée. Nous supposons donc qu’elle retourne un résultat valide. Voici d’ailleurs ce qu’elle retourne si elle reçoit en entrée dix mille observations générées aléatoirement selon une loi normale standard et que nous lui demandons d’effectuer une estimation de densité en 17 points entre -4 et 4 (la séquence des nombres entre -4 et 4 inclusivement, par bonds de 0.5).

# Simulation des observations
x <- rnorm(10000)
# Points pour lesquels nous souhaitons estimer la densité
xpts <- seq(from = -4, to = 4, length.out = 17)
# Résultat obtenu
densite_kdl <- ksmooth_double_loop(x = x, xpts = xpts, h = 1)
# Graphique
hist(
  x = x, 
  freq = FALSE, 
  ylab = "densité",
  main = "Densité empirique d'un échantillon aléatoire tiré d'une distribution N(0, 1)",
  cex.main = 0.9
)
lines(x = xpts, y = densite_kdl)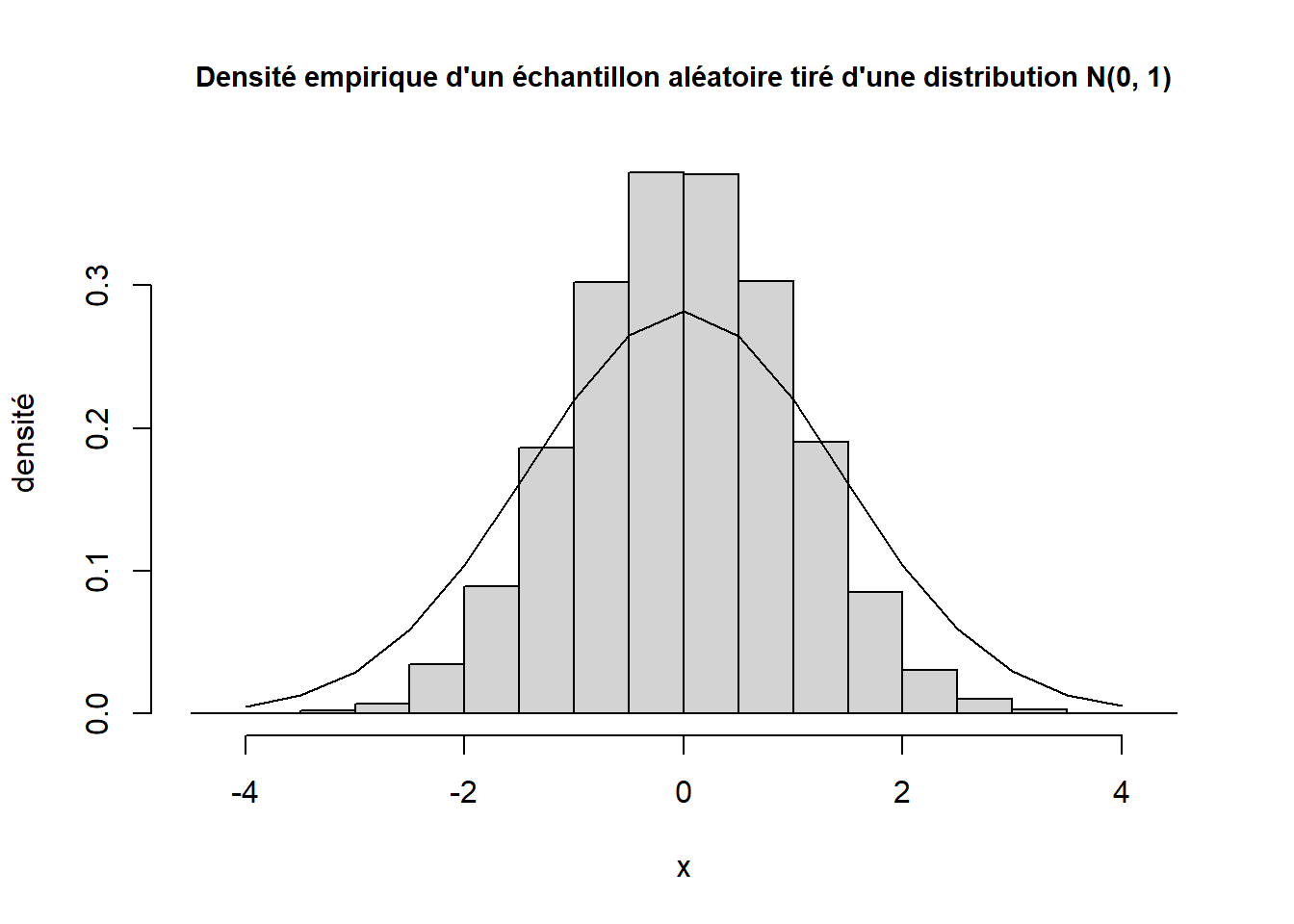

2.1 Astuce 1 : Utiliser des fonctions optimisées

Lorsque nous devons effectuer une tâche pour laquelle une fonction optimisée en temps de calcul existe déjà, il est préférable d’utiliser cette fonction. R est un logiciel libre. Le partage de code fait partie de la philosophie première du logiciel. Et cette réutilisation peut nous faire économiser beaucoup de temps.

Par exemple, est-ce que la fonction density, provenant du package stats, est plus rapide que la fonction ksmooth_double_loop?

Premièrement, convainquons-nous que les deux fonctions peuvent effectuer le même calcul. Réutilisons les vecteurs x et xpts créés ci-dessus. La commande suivante :

densite_kdl <- ksmooth_double_loop(x = x, xpts = xpts, h = 1)

lance pratiquement le même calcul que cette commande :

densite_d <- density(
  x = x,
  bw = 1,
  kernel = "gaussian",
  from = -4, to = 4, n = 17
)

Rappelons que xpts avait été défini comme suit :

xpts <- seq(from = -4, to = 4, length.out = 17)

d’où le choix des valeurs fournies aux arguments from, to et n de density.

Comparons maintenant les valeurs obtenues.

all.equal(densite_kdl, densite_d$y)
## [1] "Mean relative difference: 0.0009604423"

Il y a de très petites différences entre les valeurs, parce que le paramètre de lissage h de ksmooth_double_loop n’est pas tout à fait définit comme le paramètre bw de la fonction density. Cependant, ces différences sont tellement petites que nous pouvons tout de même considérer que les deux fonctions effectuent le même calcul.

Comparons les temps d’exécution des deux fonctions.

ex_astuce_1 <- mark(
  ksmooth_double_loop = ksmooth_double_loop(x = x, xpts = xpts, h = 1),
  density = density(x = x, bw = 1, kernel = "gaussian", from = -4, to = 4, n = 17), 
  min_iterations = 10, time_unit = "ms", check = FALSE
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(ex_astuce_1)
##            expression n_itr      min   median mem_alloc n_gc
## 1 ksmooth_double_loop    10 187.3237 203.4984      184B   22
## 2             density   725   0.4889   0.5432     315KB    5

La fonction density retourne presque instantanément le résultat, alors que la fonction ksmooth_double_loop doit rouler pendant plusieurs secondes pour effectuer une estimation en 17 points, à partir de 10000 observations.

Le coeur du calcul de la fonction density est effectué par du code en langage C. C’est pour cette raison qu’elle est à ce point plus rapide que la fonction ksmooth_double_loop. Nous allons y revenir à l’astuce 6.

2.2 Astuce 2 : Faire seulement ce qui est nécessaire

L’idée derrière cette astuce est simplement de ne pas alourdir un code d’évaluations inutiles.

Par exemple, si nous voulons calculer la somme des valeurs dans chacune des colonnes d’une matrice, la fonction colSums est plus rapide que la fonction apply.

mat <- matrix(rnorm(100 * 1000), nrow = 100, ncol = 1000)
ex_astuce_2 <- mark(
  colSums(x = mat), 
  apply(X = mat, MARGIN = 2, FUN = sum),
  min_iterations = 10, time_unit = "us"
)
print_bench_mark(ex_astuce_2)
##                              expression n_itr    min median mem_alloc n_gc
## 1                      colSums(x = mat)  6947   63.5   67.5    7.86KB    1
## 2 apply(X = mat, MARGIN = 2, FUN = sum)   161 2361.7 2601.7    2.02MB    9

Ce résultat s’explique par le fait que la fonction colSums est spécialisée dans la tâche que nous cherchions à effectuer. Son code est simplifié, par rapport au code de apply qui peut appliquer n’importe quelle fonction sur n’importe quelle dimension d’un array. Nous pourrions aussi dire que la fonction colSums est une fonction optimisée.

Remarquons que la fonction apply utilise ici beaucoup plus de mémoire que la fonction colSums.

C’est cette astuce, de faire seulement ce qui est nécessaire, qui pousse certains programmeurs R à ne pas utiliser la fonction return pour retourner la sortie de leurs fonctions. L’appel à la fonction return amène une évaluation de plus à effectuer. Dans cette fiche, la fonction return n’a jamais été utilisée pour cette raison. Ne pas utiliser return comporte cependant le désavantage de rendre le code un peu moins clair.

2.3 Astuce 3 : Exploiter les calculs matriciels et vectoriels

Nous avons déjà vu qu’en effectuant des calculs matriciels et vectoriels en R, comme avec la fonction compte_impair_vectoriel, nous arrivons à faire un calcul beaucoup plus rapidement qu’avec une boucle, comme avec la fonction compte_impair_boucle. Le calcul matriciel ou vectoriel en R est optimisé pour être très rapide. En fait, ces types de calculs font intervenir des boucles, mais programmées et compilées dans un langage informatique de plus bas niveau (et donc plus rapide) que R tel que le langage C ou Fortran.

Pour illustrer une fois de plus cette astuce, étudions la performance d’une autre fonction d’estimation de densité par noyau gaussien tirée de Peng et de Leeuw (2002) : la fonction ksmooth2, ici renommée ksmooth_outer. Le corps de cette fonction ne contient aucune boucle. Il fait plutôt du calcul vectoriel en utilisant, notamment, la fonction outer.

#' @inherit ksmooth_double_loop title params return
#' @description Version 2 : utilisation de calcul vectoriel seulement
ksmooth_outer <- function(x, xpts, h) 
{
  n <- length(x)
  D <- outer(x, xpts, "-")
  K <- dnorm(D / h)
  dens <- colSums(K) / (h * n)
}

Nous aurions aussi pu coder la fonction ksmooth ainsi.

#' @inherit ksmooth_double_loop title params return
#' @description Version 3 : utilisation d'une boucle et d'un calcul vectoriel
ksmooth_loop <- function(x, xpts, h) 
{
  n <- length(x)
  dens <- double(length(xpts))
  for (i in 1:length(xpts)) {
    dens[i] <- sum(dnorm((xpts[i] - x)/h)) / (n * h)
  }
  dens
}

Cette version remplace la deuxième boucle par un calcul vectoriel, mais conserve la première boucle de ksmooth_double_loop.

Nous aurions même pu procéder comme suit.

#' @inherit ksmooth_double_loop title params return
#' @description Version 4 : utilisation d'une fonction de la
#'              famille des apply et d'un calcul vectoriel
ksmooth_apply <- function(x, xpts, h) 
{
  n <- length(x)
  sapply(
    X = xpts,
    FUN = function(xpts_i) {
      sum(dnorm((xpts_i - x) / h)) / (n * h)
    }
  )
}

Cette version remplace la seule boucle restante par l’utilisation d’une fonction de la famille des apply.

Ces trois versions effectuent bien le même calcul que ksmooth_double_loop.

densite_kdl <- ksmooth_double_loop(x = x, xpts = xpts, h = 1)
densite_ko <- ksmooth_outer(x = x, xpts = xpts, h = 1)
densite_kl <- ksmooth_loop(x = x, xpts = xpts, h = 1)
densite_ka <- ksmooth_apply(x = x, xpts = xpts, h = 1)

all.equal(densite_kdl, densite_ko)
## [1] TRUE
all.equal(densite_kdl, densite_kl)
## [1] TRUE
all.equal(densite_kdl, densite_ka)
## [1] TRUE

Comparons maintenant les temps d’exécution des quatre versions de ksmooth écrites jusqu’à maintenant.

ex_astuce_3 <- mark(min_iterations = 10, time_unit = "ms",
               v1_double_boucle = ksmooth_double_loop(x = x, xpts = xpts, h = 1), 
  v2_calcul_vectoriel_seulement = ksmooth_outer(x = x, xpts = xpts, h = 1),
  v3_boucle_et_calcul_vectoriel = ksmooth_loop(x = x, xpts = xpts, h = 1),
   v4_apply_et_calcul_vectoriel = ksmooth_apply(x = x, xpts = xpts, h = 1)
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(ex_astuce_3)
##                      expression n_itr      min   median mem_alloc n_gc
## 1              v1_double_boucle    10 175.8289 186.5701      184B   23
## 2 v2_calcul_vectoriel_seulement    35  13.0143  13.5004    6.51MB    5
## 3 v3_boucle_et_calcul_vectoriel    39  12.5244  12.6730     2.6MB    3
## 4  v4_apply_et_calcul_vectoriel    39  12.5518  12.7757    2.63MB    2

Nous constatons que les deux dernières versions sont légèrement plus rapides que la version 2 utilisant seulement du calcul vectoriel!

Ce qu’il faut retenir de ces exemples est ceci :

  • Le code le plus rapide n’est pas toujours celui que nous croyons. Il est parfois difficile de prédire quel bout de code sera le plus rapide. Ici, nous aurions pu croire que le calcul totalement vectoriel (ksmooth_outer) serait plus rapide qu’une boucle jumelée à un calcul vectoriel (ksmooth_loop). Pourtant, ksmooth_loop est légèrement plus rapide que ksmooth_outer. Il est donc toujours recommandé, lors de l’optimisation du temps d’exécution d’une fonction, d’essayer les différentes solutions possibles et de mesurer leurs temps d’exécution.

  • Les fonctions de la famille des apply ne sont pas nécessairement plus rapides qu’une boucle. Ces fonctions cachent littéralement des boucles et ne représentent pas une sorte de calcul vectoriel. Leur utilisation est recommandée principalement parce qu’elles mènent à du code plus court et plus clair selon plusieurs programmeurs R, pas à du code nécessairement plus rapide.

Remarque concernant l’utilisation de la mémoire

La fonction ksmooth_outer est environ 14 fois plus rapide que la fonction ksmooth_double_loop. Cependant, elle utilise beaucoup plus de mémoire ( 6.51MB versus 184B). Une matrice de dimension length(x) par length(xpts) est créée par la fonction. R impose une limite sur la taille des objets créés (pour plus de détails voir la fiche d’aide help("Memory-limits")). Ainsi, la fonction ksmooth_outer retourne une erreur sur mon ordinateur si je lui donne en entrée des arguments x et xpts trop grands, par exemple :

x_test <- rnorm(1000000)
xpts_test <- seq(from = -4, to = 4, length.out = 1000000)
test_memoire <- ksmooth_outer(x = x_test, xpts = xpts_test, h = 1)
## Error: cannot allocate vector of size 7450.6 Gb

alors que la fonction ksmooth_double_loop est capable de traiter ces vecteurs.

# Attention : ne pas rouler, long à exécuter
test_memoire <- ksmooth_double_loop(x = x_test, xpts = xpts_test, h = 1)

C’est un bon exemple de compromis à gérer entre le temps d’exécution et la quantité de mémoire utilisée pour faire des calculs. Un programme peut être très rapide, mais créer un objet potentiellement de taille trop grande pour être stocké en mémoire. Étant donné que notre priorité est un code fonctionnel, il faut s’assurer de ne pas aller au-delà des limites de la mémoire de notre ordinateur. Alors, dans l’optimisation du temps d’exécution, il ne faut pas oublier de garder le contrôle sur la taille des objets créés par notre programme.

2.4 Astuce 4 : Éviter les allocations de mémoire inutiles

Allouer de l’espace dans la mémoire d’un ordinateur est une opération coûteuse en temps. Deux opérations plutôt anodines sont à éviter dans une boucle R, car elles provoquent une ou des allocations en mémoire à chaque itération et ralentissent donc beaucoup la boucle. Il s’agit de :

  1. l’utilisation d’un objet de dimension croissante,
  2. l’assignation de valeur(s) à un ou des éléments d’un data frame.

2.4.1 Objets de dimension croissante

Un objet de dimension croissante est, par exemple, une matrice à laquelle nous ajoutons, à chaque itération d’une boucle, une ligne avec rbind ou une colonne avec cbind, comme le fait l’instruction suivante :

matrice <- rbind(matrice, nouvelle_ligne)

Avec un vecteur, une instruction similaire ferait plutôt appel à la fonction c ou append comme suit :

vecteur <- c(vecteur, nouvel_element)

Le problème avec ces assignations est qu’elles modifient la dimension d’un objet. L’objet ne requiert donc plus la même quantité d’espace mémoire. Il ne serait pas une bonne idée de simplement utiliser les cases mémoires adjacentes pour agrandir l’objet, car ces cases mémoires sont potentiellement utilisées pour stocker d’autres objets R ou n’importe quelle valeur nécessaire à un processus en cours d’exécution sur l’ordinateur. L’ordinateur doit plutôt complètement déplacer l’objet dans de nouvelles cases mémoire qu’il sait être inutilisées afin de ne pas entrer en conflit avec quoi que ce soit. Ainsi, avec les commandes précédentes, nous avons peut-être l’impression de modifier le contenu de certaines cases mémoire alors qu’en réalité nous provoquons une nouvelle allocation de mémoire.

Exemple :

Simulons une expérience aléatoire dans laquelle nous lançons un dé et additionnons les valeurs obtenues. L’expérience s’arrête lorsqu’une certaine somme cumulative des résultats a été atteinte.

La première fonction que nous allons créer pour simuler cette expérience va utiliser un objet de dimension croissante pour garder une trace des résultats.

#' @title Simulation de lancers d'un dé pour atteindre une somme visée
#' @description Version utilisant un vecteur de taille croissante pour stocker les résultats
#' @param somme_visee somme cumulative de valeurs obtenues à atteindre (par défaut 50000)
#' @return vecteur des résultats de tous les lancers de dé
somme_de_vecteur_croissant <- function(somme_visee = 50000){
  somme <- 0
  resultats <- integer(length = 0)  # ou resultats <- NULL
  while (somme < somme_visee) {
    tirage <- sample(1:6, size = 1)
    somme <- somme + tirage
    resultats <- c(resultats, tirage)
  }
  resultats
}

La deuxième fonction que nous allons créer pour simuler cette expérience va plutôt utiliser un grand objet de taille fixe pour stocker les résultats.

#' @inherit somme_de_vecteur_croissant title params return
#' @description Version utilisant un vecteur de taille fixe pour stocker les résultats
somme_de_vecteur_fixe <- function(somme_visee = 50000){
  somme <- 0
  resultats <- integer(somme_visee)
  i <- 0
  while(somme < somme_visee) {
    tirage <- sample(1:6, size = 1)
    somme <- somme + tirage
    i <- i + 1
    resultats[i] <- tirage
  }
  resultats[1:i]
}

Nous ne savons pas d’avance combien de lancers de dé devront être effectués pour atteindre une somme de somme_visee, mais nous savons que ce sera au maximum somme_visee lancers, puisque le plus petit résultat du lancer d’un dé est 1. Ainsi, nous créons d’abord un très grand vecteur, de longueur somme_visee, et nous allons modifier les éléments de ce vecteur à chaque itération de la boucle (une itération = un lancer de dé). Nous modifions d’abord le premier élément puis le deuxième et ainsi de suite, grâce à l’indicateur de position i que nous incrémentons de 1 à chaque itération. À la fin, nous retournons seulement les éléments du vecteur de résultat qui ont été modifiés.

Comparons les temps d’exécution des deux fonctions pour l’atteinte d’une somme de 50000.

ex_dim_crois <- mark(
  somme_de_vecteur_croissant(), 
  somme_de_vecteur_fixe(),
  min_iterations = 10, time_unit = "ms", check = FALSE
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(ex_dim_crois)
##                     expression n_itr      min    median mem_alloc n_gc
## 1 somme_de_vecteur_croissant()    10 254.5291 336.39325     418MB  142
## 2      somme_de_vecteur_fixe()    10  65.0324  70.59515      35MB    8

Nous constatons donc qu’en termes de temps de calcul, et même en termes de quantité de mémoire utilisée, il est ici préférable de créer un très grand objet, de le remplir, puis de mettre de côté les éléments inutilisés que de faire croître la taille d’un objet. C’est de la préallocation de mémoire. Par contre, encore là, il y a une limite à la grandeur de l’objet qui peut être créé.

2.4.2 Modification d’éléments dans un data frame

Lorsque nous modifions les éléments d’un objet R dans une boucle, comme nous avons fait dans la fonction somme_de_vecteur_fixe par l’instruction suivante :

resultats[i] <- tirage

la modification s’effectue sans réallocation de mémoire à chaque itération si :

  • l’objet en question est un objet atomique (vecteur, matrice ou array) ou une liste;
  • la valeur assignée est du même type que les éléments de l’objet initialisé (dans le cas d’un objet atomique);
  • l’objet possède au moins autant d’éléments que le nombre d’itérations effectuées.

Pour nous en convaincre, faisons quelques tests en utilisant la fonction tracemem qui affiche un message à chaque fois qu’un objet est copié en mémoire.

Voici une boucle qui modifie les éléments d’une matrice.

matrice <- matrix(NA_integer_, nrow = 4, ncol = 5)
tracemem(matrice)
[1] "<0000000019C9B820>"
for (i in 1:5){
  matrice[, i] <- 1:4
}
tracemem[0x0000000019c9b820 -> 0x0000000019f53170]: 
untracemem(matrice)

L’objet matrice est copié une seule fois, au début de la boucle, mais pas à chaque itération.

Nous observons le même comportement avec une liste.

liste <- vector(mode = "list", length = 5)
tracemem(liste)
[1] "<000000001A2DC048>"
for (i in 1:5){
  liste[[i]] <- 1:4
}
tracemem[0x000000001a2dc048 -> 0x0000000019d88738]: 
untracemem(liste)

Cependant, R se comporte différemment lors de la modification d’un élément dans un data frame

df <- as.data.frame(matrix(NA_integer_, nrow = 4, ncol = 5))
tracemem(df)
[1] "<00000176DC803D98>"
for (i in 1:5){
  df[, i] <- 1:4
}
tracemem[0x00000176dc803d98 -> 0x00000176dc193028]: 
tracemem[0x00000176dc193028 -> 0x00000176dc193178]: [<-.data.frame [<- 
tracemem[0x00000176dc193178 -> 0x00000176dc1932c8]: [<-.data.frame [<- 
tracemem[0x00000176dc1932c8 -> 0x00000176dc193418]: [<-.data.frame [<- 
tracemem[0x00000176dc193418 -> 0x00000176dc193568]: [<-.data.frame [<- 
tracemem[0x00000176dc193568 -> 0x00000176dc1936b8]: [<-.data.frame [<- 
untracemem(df)

L’objet df est copié au début de la boucle, puis il est recopié une fois à chaque itération. Ces allocations de mémoire répétées prennent du temps.

La lenteur des opérations de manipulation de data frame est bien connue en R. Des alternatives plus rapides existent, notamment les data tables offerts par le package data.table. Ce package a été mentionné à quelques reprises dans ce cours, notamment dans les notes sur le prétraitement de données en R. Certaines fonctions de ce package permettent la modification de data table « par référence », donc sans créer de copies de l’objet et nécessiter des allocations de mémoire.

Reprenons l’exemple de la simulation d’une expérience aléatoire de lancers d’un dé jusqu’à l’atteinte d’une certaine somme cumulative des valeurs obtenues. Voici deux autres fonctions réalisant cette expérience, qui diffèrent seulement par le type de l’objet utilisé pour stocker les résultats. La fonction somme_de_data_frame utilise un data frame, la fonction somme_de_matrice une matrice et la fonction somme_de_data_table un data table.

#' @title Simulation de lancers d'un dé pour atteindre une somme visée
#' @description Version utilisant un data frame pour stocker les résultats
#' @param somme_visee somme cumulative de valeurs obtenues à atteindre (par défaut 50000)
#' @return data frame possédant une ligne par lancer, contenant le numéro de lancer
#'         dans la première colonne et le résultat obtenu dans la deuxième colonne
somme_de_data_frame <- function(somme_visee = 50000){
  resultats <- as.data.frame(matrix(NA_integer_, ncol = 2, nrow = somme_visee))
  resultats[, 1] <- 1:somme_visee  # Colonne 1 = numéro de l'itération
  somme <- 0
  i <- 0
  while (somme < somme_visee) {
    tirage <- sample(1:6, size = 1)
    somme <- somme + tirage
    i <- i + 1
    resultats[i, 2] <- tirage  # Colonne 2 = résultat obtenu au lancer du dé
  }
  resultats[1:i, ]
}
#' @inherit somme_de_data_frame title params
#' @description Version utilisant une matrice pour stocker les résultats
#' @return matrice possédant une ligne par lancer, contenant le numéro de lancer
#'         dans la première colonne et le résultat obtenu dans la deuxième colonne
somme_de_matrice <- function(somme_visee = 50000){
  resultats <- matrix(NA_integer_, ncol = 2, nrow = somme_visee)
  resultats[, 1] <- 1:somme_visee  # Colonne 1 = numéro de l'itération
  somme <- 0
  i <- 0
  while (somme < somme_visee) {
    tirage <- sample(1:6, size = 1)
    somme <- somme + tirage
    i <- i + 1
    resultats[i, 2] <- tirage  # Colonne 2 = résultat obtenu au lancer du dé
  }
  resultats[1:i, ]
}
#' @inherit somme_de_data_frame title params
#' @description Version utilisant un data table pour stocker les résultats
#' @return data table possédant une ligne par lancer, contenant le numéro de lancer
#'         dans la première colonne et le résultat obtenu dans la deuxième colonne
somme_de_data_table <- function(somme_visee = 50000){
  resultats <- data.table::as.data.table(matrix(NA_integer_, ncol = 2, nrow = somme_visee))
  data.table::set(resultats, j = 1L, value = 1:somme_visee)
  somme <- 0L
  i <- 0L
  while (somme < somme_visee) {
    tirage <- sample(1:6, size = 1)
    somme <- somme + tirage
    i <- i + 1L
    data.table::set(resultats, i = i, j = 2L, value = tirage)
  }
  resultats[1:i, ]
}

Dans la fonction somme_de_data_table, nous avons pris soin de modifier le data table par référence en utilisant la fonction set du package data.table.

Quelle fonction est la plus rapide?

ex_compar_df <- mark(
  somme_de_data_frame(),
  somme_de_matrice(),
  somme_de_data_table(),
  min_iterations = 10, time_unit = "ms", check = FALSE
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(ex_compar_df)
##              expression n_itr      min    median mem_alloc n_gc
## 1 somme_de_data_frame()    10 767.9073 840.09420    2.69GB  473
## 2    somme_de_matrice()    10  59.8008  65.13605    35.5MB    8
## 3 somme_de_data_table()    10 189.3442 198.42650   39.78MB   25

Ici, l’utilisation du data frame est environ 13 fois plus lente que l’utilisation d’une matrice (et utilise plus de mémoire)! L’utilisation d’un data table est un peu plus lente que l’utilisation d’une matrice, mais le data table a l’avantage de pouvoir stocker des données de types différents entre ses colonnes.

Le message à retenir ici est, qu’autant que possible, il vaut mieux éviter d’utiliser un data frame pour stocker des résultats générés dans une boucle.

2.5 Astuce 5 : Faire du calcul en parallèle

Une importante technique pour réaliser des calculs informatiques plus rapidement est le calcul en parallèle. Il s’agit d’un type de calcul qui, dans sa version la plus simple,

  • brise un long calcul en petits blocs de calcul indépendants;
  • réalise ces blocs de calcul sur plusieurs unités de calcul, simultanément (donc en parallèle);
  • rassemble à la fin tous les résultats.

Les unités de calcul utilisées peuvent être localisées sur CPU (pour Central Processing Unit) ou sur GPU (pour Graphical Processing Unit). Nous pouvons exploiter différentes unités sur une seule machine ou encore sur plusieurs noeuds de calcul dans une grappe de serveurs.

Je vais réaliser un exemple dans lequel je vais exploiter tous les coeurs du CPU de mon ordinateur.

Il existe un très grand nombre de packages R pour réaliser du calcul en parallèle (https://cran.r-project.org/web/views/HighPerformanceComputing.html). Un de ces packages vient avec l’installation de R. Il s’agit du package parallel. Ce package est donc déjà installé sur votre ordinateur si R y est installé. Cependant, le package n’est pas chargé par défaut lors de l’ouverture d’une nouvelle session R. Chargeons-le.

library(parallel)

Tout d’abord, voyons combien de coeurs compte mon ordinateur.

detectCores()
## [1] 4

Il compte 4 coeurs logiques.

Maintenant, si nous travaillons sous Windows, il faut d’abord établir une connexion entre R est les différents coeurs avec la fonction makeCluster.

coeurs <- detectCores()
grappe <- makeCluster(coeurs - 1)
grappe
## socket cluster with 3 nodes on host 'localhost'

Notons que la première fois que j’ai soumis cette commande, Windows m’a demandé une autorisation.

Remarquons aussi que je n’ai utilisé que 3 des 4 coeurs disponibles sur mon ordinateur dans le but de laisser un coeur libre pour les autres processus actifs.

Ensuite, je vais comparer la fonction ksmooth_apply, qui utilise sapply, à une autre version de ksmooth qui utilise la version parallèle du sapply offerte par le package parallel, nommée parSapply.

#' @inherit ksmooth_double_loop title params return
#' @description Version 5 : utilisation de parSapply et d'un calcul vectoriel
ksmooth_parallel <- function(grappe, x, xpts, h)
{
  n <- length(x)
  parSapply(
    cl = grappe,
    X = xpts,
    FUN = function(xpts_i) {
      sum(dnorm((xpts_i - x) / h)) / (n * h)
    }
  )
}

Ces fonctions effectuent bien le même calcul.

densite_ka <- ksmooth_apply(x = x, xpts = xpts, h = 1)
densite_kp <- ksmooth_parallel(grappe = grappe, x = x, xpts = xpts, h = 1)

all.equal(densite_ka, densite_kp)
## [1] TRUE

Laquelle est la plus rapide?

ex_astuce_5 <- mark(min_iterations = 10, time_unit = "ms",
     v4_sapply = ksmooth_apply(x = x, xpts = xpts, h = 1), 
  v5_parSapply = ksmooth_parallel(grappe = grappe, x = x, xpts = xpts, h = 1)
)
print_bench_mark(ex_astuce_5)
##     expression n_itr     min   median mem_alloc n_gc
## 1    v4_sapply    38 12.5410 12.70390     2.6MB    1
## 2 v5_parSapply    64  7.1775  7.62145   121.5KB    0

Le calcul en parallèle a permis de réduire un peu le temps d’exécution. Même si 3 coeurs ont été exploités, le calcul n’est pas 3 fois plus rapide, car :

  • mon ordinateur possède en fait 2 coeurs physiques, chacun séparé en 2 coeurs logiques (pour un total de 4 coeurs logiques), et des coeurs logiques ne sont pas aussi rapides que des coeurs physiques;
  • toutes les communications entre les coeurs et R requièrent aussi un peu de temps.

Une fois le calcul terminé, il est recommandé de fermer les connexions entre R et les coeurs de calcul avec la fonction stopCluster.

stopCluster(grappe)

Nous aurions pu aller chercher une amélioration plus importante du temps de calcul en utilisant plus d’unités de calcul. Le département de mathématiques et de statistique possède une grappe de calcul pouvant être utilisée par les étudiants du département pour faire du calcul en parallèle. Calcul Québec gère aussi des supercalculateurs pour le calcul en parallèle utilisable gratuitement par tout chercheur (et ses étudiants) admissible aux subventions provenant des conseils de recherche canadiens, à la condition d’avoir obtenu des accès aux ressources : https://www.calculquebec.ca/services-aux-chercheurs/infrastructures-et-services/. Finalement, plusieurs plateformes de cloud computing permettent d’utiliser des serveurs de calculs à faible coût (par exemple Amazon Web Services, Microsoft Azure, Google Cloud Platform).

Lancer des calculs en parallèle sur une grappe de calcul ne s’effectue pas tout à fait comme le lancement de calculs en parallèle sur une seule machine. La communication avec la grappe s’effectue typiquement via des protocoles SSH et les programmes R se lancent en mode batch grâce à la commande Rscript. Ce sujet ne sera pas couvert ici, car il est plutôt complexe et la mise en oeuvre de calculs en parallèle dépend des ressources à notre disposition. Pour plus d’informations, je vous réfère à un document que j’ai écrit sur le sujet, qui est disponible ici : https://stt4230.rbind.io/autre_materiel/calcul_parallele_r/.

2.6 Astuce 6 : Reprogrammer en C ou C++ les bouts de code les plus lents

Note : La matière présentée dans cette section ne sera pas évaluée.

Une dernière astuce pour rendre du code R plus rapide est de reprogrammer ses bouts les plus lents en C ou C++. Le langage R étant un langage interprété, il n’est pas aussi rapide que du C ou du C++, qui sont des langages de plus bas niveau, plus près du langage machine.

Nous n’utilisons pas cette astuce pour réaliser des analyses de données plus rapidement, mais plutôt pour créer une fonction qui réalise rapidement un certain calcul.

Il existe quelques outils pour intégrer du code C ou C++ en R. Un outil très populaire pour intégrer du code C++ en R est le package Rcpp (http://www.rcpp.org/). Le R de base offre pour sa part les fonctions .C, .Call et .External pour ce faire (voir le manuel Writing R Extensions, chapitre 5). Je vais me contenter ici d’illustrer l’utilisation de la fonction .C, qui est la méthode la plus simple, mais la moins puissante.

La fonction ksmooth_double_loop peut être reprogrammée en C comme suit (Peng et de Leeuw, 2002) :

#include <R.h>
#include <Rmath.h>

void kernel_smooth(double *x, int *n, double *xpts,
       int *nxpts, double *h, double *result)
{
 int i, j;
 double d, ksum;

 for(i=0; i < *nxpts; i++) 
 {
  ksum = 0;
  for(j=0; j < *n; j++) 
  {
   d = xpts[i] - x[j];
   ksum += dnorm(d / *h, 0, 1, 0);
  }
  result[i] = ksum / ((*n) * (*h));
 }
}

Du code C destiné à être appelé en R avec la fonction .C se doit de respecter les propriétés suivantes (Peng et de Leeuw, 2002) :

  • Les fonctions C appelées en R doivent être de type « void ». Elles doivent retourner les résultats des calculs par leurs arguments.

  • Les arguments passés aux fonctions C sont des pointeurs à un nombre ou à un tableau. Il faut donc correctement déréférencer les pointeurs dans le code C afin d’obtenir la valeur d’un élément dont l’adresse est contenue dans le pointeur. Un pointeur est déréférencé en ajoutant * devant celui-ci.

  • Il est préférable d’inclure dans tout fichier contenant du code C à être appelé en R le fichier d’en-tête R.h en ajoutant au début du fichier de code C la ligne :

#include <R.h>

De plus, il est possible d’utiliser en C certaines fonctions mathématiques R en incluant le fichier d’en-tête Rmath.h dans le fichier de code C par la ligne :

#include <Rmath.h>

Les fonctions mathématiques R utilisables en C sont énumérées dans le manuel de R Writing R Extensions, chapitre 6.

  • Le fichier contenant le code C doit porter l’extension « .c ».

Une fois le code C écrit, il reste trois étapes à compléter pour intégrer du code C en R avec la fonction .C.

  1. Compiler le code C afin de créer un objet partagé si nous travaillons sur Linux ou une « bibliothèque de liens dynamiques » (an anglais DLL) si nous travaillons sur Windows ou Mac OS X ;
  2. Charger en R l’objet partagé ou le DLL créé à l’étape précédente avec la fonction dyn.load ;
  3. Appeler en R les fonctions créées dans le code C avec la fonction d’interface .C.

Retournons donc à l’exemple. Supposons que le code C ci-dessus se trouve dans le fichier C:/coursR/ksmoothC.c. Dans le terminal sous Linux ou macOS et dans une fenêtre invite de commandes sous Windows, il faut se positionner dans le répertoire contenant le fichier et lancer la commande suivante :

R CMD SHLIB ksmoothC.c

Notons qu’en RStudio, nous pouvons facilement ouvrir un terminal ou une fenêtre invite de commandes par le menu Tools > Shell….

Cette commande fonctionnera seulement si un compilateur C/C++ est installé sur l’ordinateur. Les outils nécessaires au développement de packages R en fournissent un. Si la commande a fonctionné, l’objet partagé ou le DLL sera créé. Sur Windows, il s’agit d’un fichier portant l’extension .dll.

Maintenant, chargeons cet objet en R avec la fonction dyn.load, comme dans cet exemple réalisé sur Windows :

dyn.load("C:/coursR/ksmoothC.dll")

Il ne reste plus qu’à écrire la « fonction R enveloppe », qui appelle la fonction écrite en C, comme dans cet exemple (fonction ksmooth3 de Peng et de Leeuw 2002 renommée ici ksmooth_C) :

#' @title Estimation de densité par noyau gaussien
#' @description Version 6 : code C + appel à la fonction .C
#' @inherit ksmooth_double_loop params return
ksmooth_C <- function(x, xpts, h) {
  n <- length(x)
  nxpts <- length(xpts)
  dens <- .C("kernel_smooth", as.double(x), as.integer(n),
             as.double(xpts), as.integer(nxpts), as.double(h),
             result = double(length(xpts)))
  dens$result
}

Dans l’appel à la fonction .C, le nom de la fonction doit obligatoirement être entre guillemets. Il est préférable de s’assurer que chaque argument passé à la fonction C est du bon type en appliquant aux arguments une fonction telle as.integer, as.double, as.character ou as.logical.

Est-ce que la fonction ksmooth_C effectue bien le même calcul que ksmooth_double_loop?

densite_kdl <- ksmooth_double_loop(x = x, xpts = xpts, h = 1)
densite_kC <- ksmooth_C(x = x, xpts = xpts, h = 1)

all.equal(densite_kdl, densite_kC)
## [1] TRUE

Oui.

Maintenant, voyons si cette nouvelle version de ksmooth est plus rapide que certaines des autres fonctions que nous avons développées. Comparons aussi ksmooth_C à la fonction density

ex_astuce_6 <- mark(
  ksmooth_double_loop = ksmooth_double_loop(x = x, xpts = xpts, h = 1), 
  ksmooth_outer = ksmooth_outer(x = x, xpts = xpts, h = 1),
  ksmooth_loop = ksmooth_loop(x = x, xpts = xpts, h = 1),
  ksmooth_C = ksmooth_C(x = x, xpts = xpts, h = 1),
  density = density(x = x, bw = 1, kernel = "gaussian", from = -4, to = 4, n = 17),
  min_iterations = 10, time_unit = "ms", check = FALSE
)
## Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print_bench_mark(ex_astuce_6)
##            expression n_itr      min   median mem_alloc n_gc
## 1 ksmooth_double_loop    10 181.5444 190.4726      184B   26
## 2       ksmooth_outer    37  13.0084  13.3512    6.49MB    3
## 3        ksmooth_loop    39  12.5023  12.6614     2.6MB    2
## 4           ksmooth_C    48  10.0945  10.2055  112.05KB    0
## 5             density   907   0.4845   0.4987  315.33KB    4

La fonction ksmooth_C bat ksmooth_double_loop (double boucle), ksmooth_outer (calcul vectoriel seul avec outer) et ksmooth_loop (boucle et calcul vectoriel), quoiqu’elle n’est pas beaucoup plus rapide que ces deux dernières. Cependant, density demeure beaucoup plus rapide que tout ce que nous avons programmé.

Mais pourquoi density est-il tellement plus rapide alors qu’elle fait appel à du code C, tout comme ksmooth_C? Premièrement, parce que ce code C est interfacé en R par la fonction .Call plutôt que .C. L’interface .Call est plus compliquée d’utilisation que .C, mais plus efficace. La fonction density est aussi plus rapide parce que son code C a lui aussi été optimisé.

3 Résumé

Optimisation de temps d’exécution

Outils pour analyser la performance d’un programme R :

  • calcul global de temps d’exécution :
    • la fonction system.time (R de base),
    • la fonction mark du package bench;
  • calcul plus détaillé de temps d’exécution :
    • par fonction appelée (call stack) : les fonctions Rprof et summaryRprof (R de base),
    • par ligne de code : la fonction profvis (package du même nom).

Conseil : comparaison de différentes options.
\(\longrightarrow\) Le code le plus rapide n’est pas toujours celui que nous croyons.

Contrainte : compromis temps d’exécution - quantité de mémoire utilisée

Stratégies d’optimisation du temps d’exécution

Astuces pour du code R plus rapide :

  1. Utiliser des fonctions optimisées
  2. Faire seulement ce qui est nécessaire
  3. Exploiter les calculs matriciels et vectoriels
  4. Éviter les allocations de mémoire inutiles
  5. Faire du calcul en parallèle
  6. Reprogrammer en C ou C++ les bouts de code les plus lents
Astuce 1 : Utiliser des fonctions optimisées

Profiter du travail des autres

Le web regorge de fonctions R : la distribution de base de R, le CRAN, Bioconductor, GitHub, etc.

Astuce 2 : Faire seulement ce qui est nécessaire

Ne pas alourdir son code d’évaluations inutiles

Astuce 3 : Exploiter les calculs matriciels et vectoriels

R est optimisé pour le calcul vectoriel

(fonctions de la famille des apply = boucles, pas calcul vectoriel)

Astuce 4 : Éviter les allocations de mémoire inutiles

Allouer de l’espace dans la mémoire d’un ordinateur = opération coûteuse en temps

Opérations à éviter dans une boucle R :

  1. utilisation d’un objet de dimension croissante : utiliser plutôt un objet de taille fixe;
  2. assignation de valeur(s) dans un data frame : utiliser plutôt un objet atomique ou un data table.
Astuce 5 : Faire du calcul en parallèle

Version la plus simple du calcul en parallèle :

  • brise un long calcul en petits blocs de calcul indépendants;
  • réalise ces blocs de calcul sur plusieurs unités de calcul (coeurs d’un processeur) simultanément (donc en parallèle);
  • rassemble à la fin tous les résultats.

Domaine très large : https://cran.r-project.org/web/views/HighPerformanceComputing.html

Domaine très technique : dépend des ressources à notre portée (CPU versus GPU, plusieurs coeurs sur notre ordinateur, grappe de serveurs de calcul, plateforme de cloud computing, etc.)

Point de départ en R : package parallel

Astuce 6 : Reprogrammer en C ou C++ les bouts de code les plus lents

Meilleure solution pour développer une fonction très rapide, pas pour réaliser rapidement des analyses de données.

  • fonction d’interface .C,
  • fonction d’interface .Call ou .External,
  • package Rcpp pour l’intégration de code C++.

Références

Référence citée dans le texte :

[1] Matloff, N. (2011). The Art of R Programming: A Tour of Statistical Software Design. No Starch Press. Sections 1.3 et 7.4

Références supplémentaires :